Traveling Salesman Problem: Solver-Based

Open Live Script

This example shows how to use binary integer programming to solve the classic traveling salesman problem. This problem involves finding the shortest closed tour (path) through a set of stops (cities). In this case there are 200 stops, but you can easily change the nStops variable to get a different problem size. You'll solve the initial problem and see that the solution has subtours. This means the optimal solution found doesn't give one continuous path through all the points, but instead has several disconnected loops. You'll then use an iterative process of determining the subtours, adding constraints, and rerunning the optimization until the subtours are eliminated.

For the problem-based approach, see Traveling Salesman Problem: Problem-Based.

Problem Formulation

Formulate the traveling salesman problem for integer linear programming as follows:

Generate all possible trips, meaning all distinct pairs of stops.
Calculate the distance for each trip.
The cost function to minimize is the sum of the trip distances for each trip in the tour.
The decision variables are binary, and associated with each trip, where each 1 represents a trip that exists on the tour, and each 0 represents a trip that is not on the tour.
To ensure that the tour includes every stop, include the linear constraint that each stop is on exactly two trips. This means one arrival and one departure from the stop.

Generate Stops

Generate random stops inside a crude polygonal representation of the continental U.S.

load('usborder.mat','x','y','xx','yy');
rng(3,'twister') % Makes a plot with stops in Maine & Florida, and is reproducible
nStops = 200; % You can use any number, but the problem size scales as N^2
stopsLon = zeros(nStops,1); % Allocate x-coordinates of nStops
stopsLat = stopsLon; % Allocate y-coordinates
n = 1;
while (n <= nStops)
    xp = rand*1.5;
    yp = rand;
    if inpolygon(xp,yp,x,y) % Test if inside the border
        stopsLon(n) = xp;
        stopsLat(n) = yp;
        n = n+1;
    end
end

Calculate Distances Between Points

Because there are 200 stops, there are 19,900 trips, meaning 19,900 binary variables (# variables = 200 choose 2).

Generate all the trips, meaning all pairs of stops.

idxs = nchoosek(1:nStops,2);

Calculate all the trip distances, assuming that the earth is flat in order to use the Pythagorean rule.

dist = hypot(stopsLat(idxs(:,1)) - stopsLat(idxs(:,2)), ...
             stopsLon(idxs(:,1)) - stopsLon(idxs(:,2)));
lendist = length(dist);

With this definition of the dist vector, the length of a tour is

dist'*x_tsp

where x_tsp is the binary solution vector. This is the distance of a tour that you try to minimize.

Create Graph and Draw Map

Represent the problem as a graph. Create a graph where the stops are nodes and the trips are edges.

G = graph(idxs(:,1),idxs(:,2));

Display the stops using a graph plot. Plot the nodes without the graph edges.

figure
hGraph = plot(G,'XData',stopsLon,'YData',stopsLat,'LineStyle','none','NodeLabel',{});
hold on
% Draw the outside border
plot(x,y,'r-')
hold off

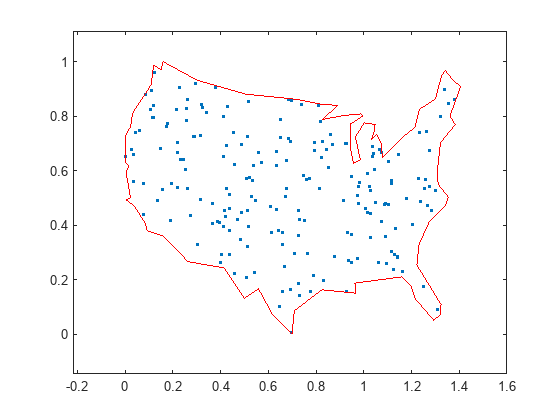
Figure contains an axes object. The axes object contains 2 objects of type graphplot, line.

Constraints

Create the linear constraints that each stop has two associated trips, because there must be a trip to each stop and a trip departing each stop. This formulation works when the problem has at least three stops.

Aeq = spalloc(nStops,size(idxs,1),nStops*(nStops-1)); % Allocate a sparse matrix
for ii = 1:nStops
    whichIdxs = (idxs == ii); % Find the trips that include stop ii
    whichIdxs = sparse(sum(whichIdxs,2)); % Include trips where ii is at either end
    Aeq(ii,:) = whichIdxs'; % Include in the constraint matrix
end
beq = 2*ones(nStops,1);

Binary Bounds

All decision variables are binary. Now, set the intcon argument to the number of decision variables, put a lower bound of 0 on each, and an upper bound of 1.

intcon = 1:lendist;
lb = zeros(lendist,1);
ub = ones(lendist,1);

Optimize Using intlinprog

The problem is ready for solution. To suppress iterative output, turn off the default display.

opts = optimoptions('intlinprog','Display','off');
[x_tsp,costopt,exitflag,output] = intlinprog(dist,intcon,[],[],Aeq,beq,lb,ub,opts);

Create a new graph with the solution trips as edges. To do so, round the solution in case some values are not exactly integers, and convert the resulting values to logical.

x_tsp = logical(round(x_tsp));
Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2),[],numnodes(G));
% Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2)); % Also works in most cases

Visualize Solution

hold on
highlight(hGraph,Gsol,'LineStyle','-')
title('Solution with Subtours')

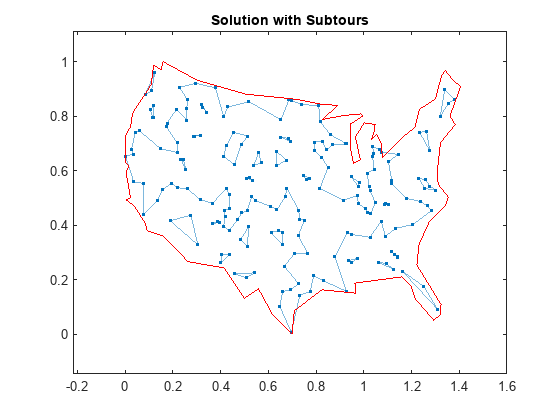
Figure contains an axes object. The axes object with title Solution with Subtours contains 2 objects of type graphplot, line.

As can be seen on the map, the solution has several subtours. The constraints specified so far do not prevent these subtours from happening. In order to prevent any possible subtour from happening, you would need an incredibly large number of inequality constraints.

Subtour Constraints

Because you can't add all of the subtour constraints, take an iterative approach. Detect the subtours in the current solution, then add inequality constraints to prevent those particular subtours from happening. By doing this, you find a suitable tour in a few iterations.

Eliminate subtours with inequality constraints. An example of how this works is if you have five points in a subtour, then you have five lines connecting those points to create the subtour. Eliminate this subtour by implementing an inequality constraint to say there must be less than or equal to four lines between these five points.

Even more, find all lines between these five points, and constrain the solution not to have more than four of these lines present. This is a correct constraint because if five or more of the lines existed in a solution, then the solution would have a subtour (a graph with $n$ nodes and $n$ edges always contains a cycle).

Detect the subtours by identifying the connected components in Gsol, the graph built with the edges in the current solution. conncomp returns a vector with the number of the subtour to which each edge belongs.

tourIdxs = conncomp(Gsol);
numtours = max(tourIdxs); % number of subtours
fprintf('# of subtours: %d\n',numtours);

# of subtours: 27

Include the linear inequality constraints to eliminate subtours, and repeatedly call the solver, until just one subtour remains.

A = spalloc(0,lendist,0); % Allocate a sparse linear inequality constraint matrix
b = [];
while numtours > 1 % Repeat until there is just one subtour
    % Add the subtour constraints
    b = [b;zeros(numtours,1)]; % allocate b
    A = [A;spalloc(numtours,lendist,nStops)]; % A guess at how many nonzeros to allocate
    for ii = 1:numtours
        rowIdx = size(A,1) + 1; % Counter for indexing
        subTourIdx = find(tourIdxs == ii); % Extract the current subtour
%         The next lines find all of the variables associated with the
%         particular subtour, then add an inequality constraint to prohibit
%         that subtour and all subtours that use those stops.
        variations = nchoosek(1:length(subTourIdx),2);
        for jj = 1:length(variations)
            whichVar = (sum(idxs==subTourIdx(variations(jj,1)),2)) & ...
                       (sum(idxs==subTourIdx(variations(jj,2)),2));
            A(rowIdx,whichVar) = 1;
        end
        b(rowIdx) = length(subTourIdx) - 1; % One less trip than subtour stops
    end

    % Try to optimize again
    [x_tsp,costopt,exitflag,output] = intlinprog(dist,intcon,A,b,Aeq,beq,lb,ub,opts);
    x_tsp = logical(round(x_tsp));
    Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2),[],numnodes(G));
    % Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2)); % Also works in most cases
    
    % Visualize result
    hGraph.LineStyle = 'none'; % Remove the previous highlighted path
    highlight(hGraph,Gsol,'LineStyle','-')
    drawnow
    
    % How many subtours this time?
    tourIdxs = conncomp(Gsol);
    numtours = max(tourIdxs); % number of subtours
    fprintf('# of subtours: %d\n',numtours)
end

# of subtours: 20
# of subtours: 7
# of subtours: 9
# of subtours: 9
# of subtours: 3
# of subtours: 2
# of subtours: 7
# of subtours: 2
# of subtours: 1

title('Solution with Subtours Eliminated');
hold off

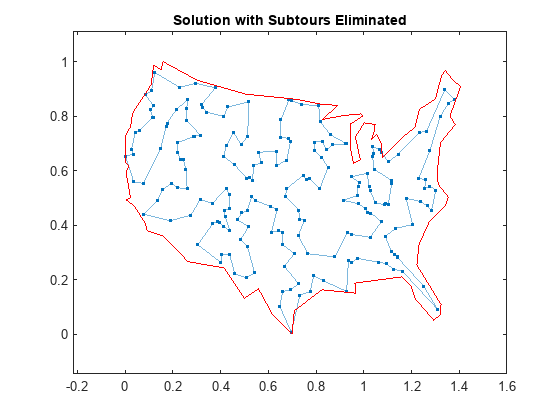
Figure contains an axes object. The axes object with title Solution with Subtours Eliminated contains 2 objects of type graphplot, line.

Solution Quality

The solution represents a feasible tour, because it is a single closed loop. But is it a minimal-cost tour? One way to find out is to examine the output structure.

disp(output.absolutegap)

The smallness of the absolute gap implies that the solution is either optimal or has a total length that is close to optimal.