Deflection Analysis of Bracket

Create Model with Geometry

The first step in solving this linear elasticity problem is to create an femodel object for structural analysis with a geometry representing a simple bracket.

model = femodel(AnalysisType="structuralStatic", ...
                Geometry="BracketWithHole.stl");

Plot Geometry

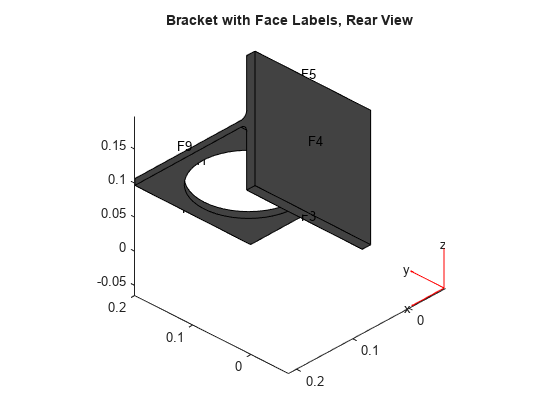
Plot the front and rear views of the geometry with face labels.

figure
pdegplot(model,FaceLabels="on");
view(30,30);
title("Bracket with Face Labels")

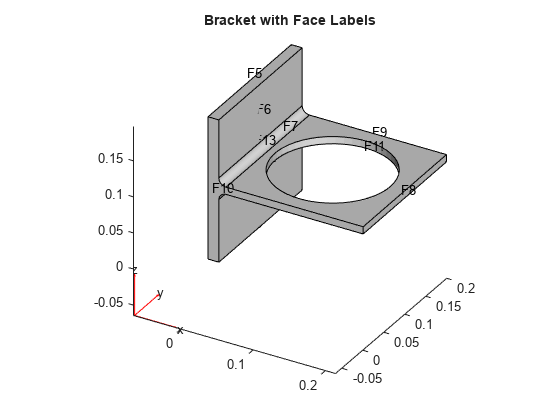
figure
pdegplot(model,FaceLabels="on");
view(-134,-32)
title("Bracket with Face Labels, Rear View")

Specify Structural Properties of Material

Specify Young's modulus and Poisson's ratio of the material.

model.MaterialProperties = ...
        materialProperties(YoungsModulus=200e9, ...
                           PoissonsRatio=0.3);

Apply Boundary Conditions and Loads

The problem has two boundary conditions: the back face (face 4) is fixed, and the front face (face 8) has an applied load. All other boundary conditions, by default, are free boundaries.

model.FaceBC(4) = faceBC(Constraint="fixed");

Apply a distributed load in the negative z-direction to the front face.

model.FaceLoad(8) = faceLoad(SurfaceTraction=[0;0;-1e4]);

Generate Mesh

Generate a mesh and assign the result to the model. This assignment updates the mesh stored in the Geometry property of the model. Plot the mesh.

model = generateMesh(model);

figure
pdemesh(model);
title("Mesh with Quadratic Tetrahedral Elements")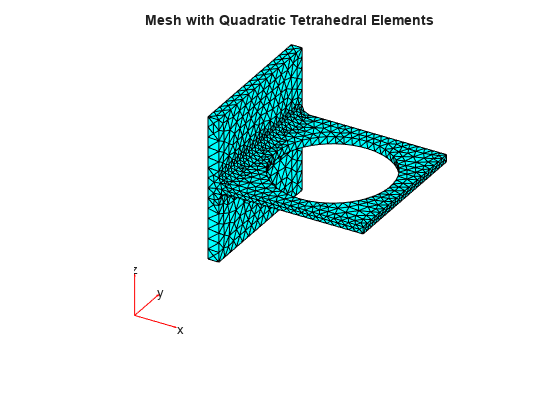

Calculate Solution

Calculate the solution by using the solve function.

result = solve(model)

result = 
  StaticStructuralResults with properties:

      Displacement: [1x1 FEStruct]
            Strain: [1x1 FEStruct]
            Stress: [1x1 FEStruct]
    VonMisesStress: [7789x1 double]
              Mesh: [1x1 FEMesh]

Examine Solution

Find the maximal deflection of the bracket in the z-direction.

minUz = min(result.Displacement.uz);
fprintf("Maximal deflection in the z-direction is %g meters.",minUz)

Maximal deflection in the z-direction is -4.46054e-05 meters.

Plot Results Interactively

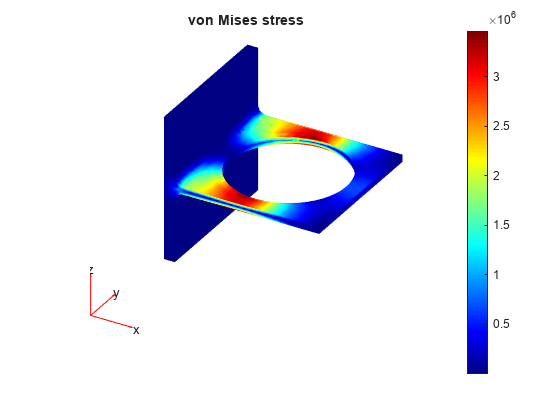
Visualize the displacement components and the von Mises stress by using the Visualize PDE Results Live Editor task. The maximal deflections are in the z-direction. Because the bracket and the load are symmetric, the x-displacement and z-displacement are symmetric, and the y-displacement is antisymmetric with respect to the center line.

First, create a new live script by clicking the New Live Script button in the File section on the Home tab.

On the Insert tab, select Task > Visualize PDE Results. This action inserts the task into your script.

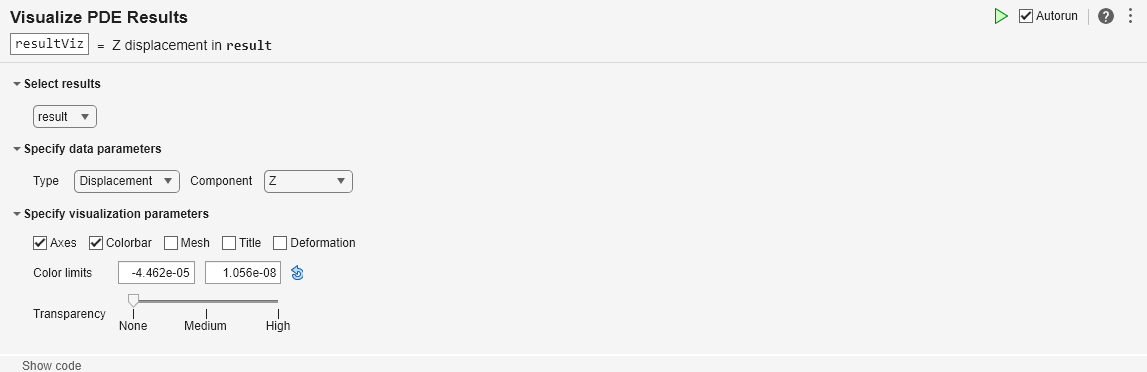
To plot the z-displacement, follow these steps. To plot the x- and y-displacements, follow the same steps, but set Component to X and Y, respectively.

Here, the blue color represents the lowest displacement value, and the red color represents the highest displacement value. The bracket load causes face 8 to dip down, so the maximum z-displacement appears blue.

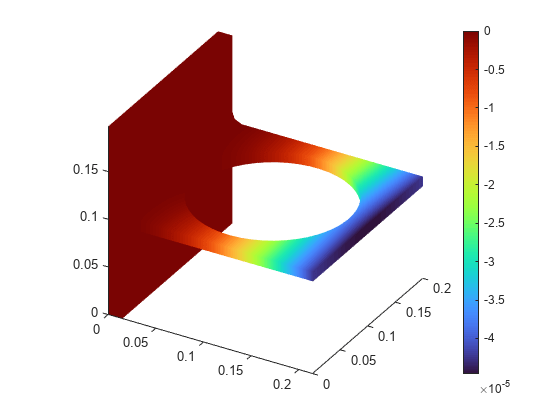
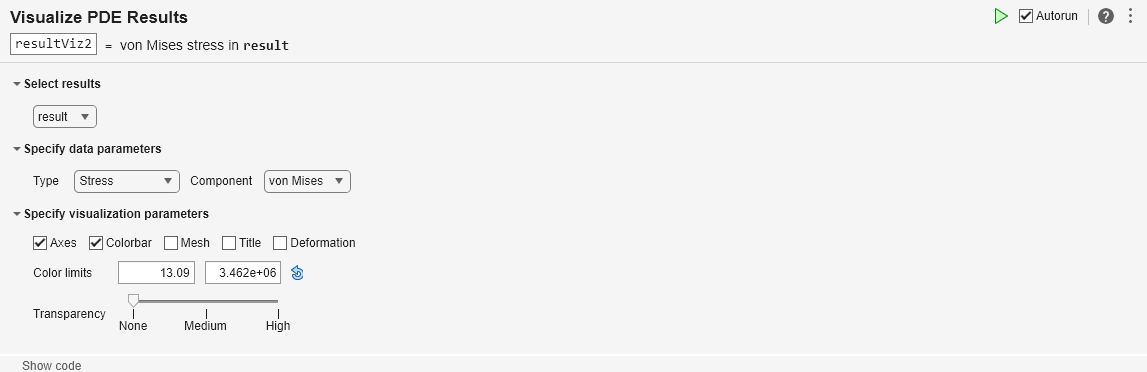
To plot the von Mises stress, in the Specify data parameters section of the task, set Type to Stress and Component to von Mises.

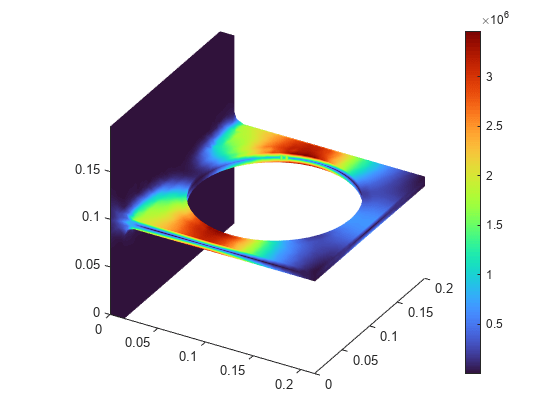
Plot Results at the Command Line

You also can plot the results, such as the displacement components and the von Mises stress, at the MATLAB® command line by using the pdeplot3D function.

figure
pdeplot3D(result.Mesh,ColorMapData=result.Displacement.ux);
title("x-displacement")
colormap("jet")

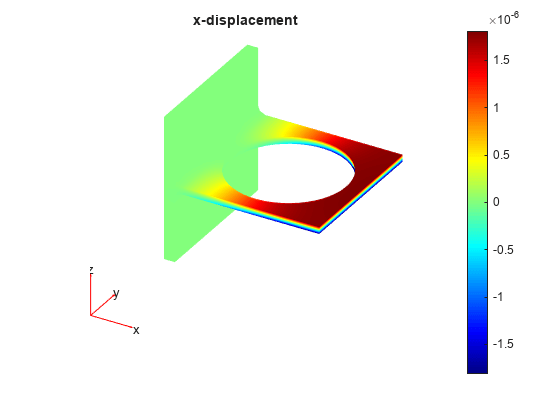
figure
pdeplot3D(result.Mesh,ColorMapData=result.Displacement.uy)
title("y-displacement")
colormap("jet")

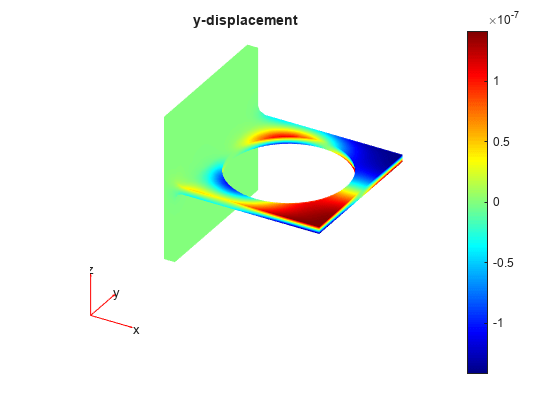
figure
pdeplot3D(result.Mesh,ColorMapData=result.Displacement.uz)
title("z-displacement")
colormap("jet")

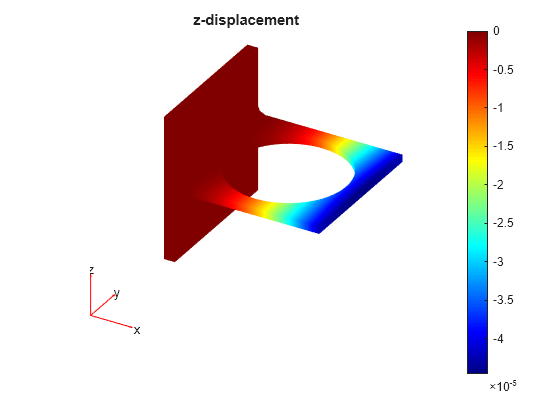
figure
pdeplot3D(result.Mesh,ColorMapData=result.VonMisesStress)
title("von Mises stress")
colormap("jet")