Geometry from Triangulated Mesh
3-D Geometry from Finite Element Mesh
This example shows how to create an fegeometry object and a DiscreteGeometry object from a 3-D mesh.
The tetmesh file, which is included in Partial Differential Equation Toolbox™, contains a 3-D tetrahedral mesh. Load the data into your workspace.
load tetmeshThe imported variable tet contains a connectivity list, and the variable X contains a matrix of points. Using these variables, create the triangulation representation.
TR = triangulation(tet,X)
TR =
triangulation with properties:
Points: [1456×3 double]
ConnectivityList: [4969×4 double]
Create an fegeometry object from the triangulation object.
gm = fegeometry(TR)
gm =
fegeometry with properties:
NumCells: 1
NumFaces: 23
NumEdges: 50
NumVertices: 30
Vertices: [30×3 double]
Mesh: [1×1 FEMesh]
The geometry contains the imported linear mesh.
gm.Mesh
ans =
FEMesh with properties:
Nodes: [3×1456 double]
Elements: [4×4969 double]
MaxElementSize: 8.2971
MinElementSize: 1.9044
MeshGradation: []
GeometricOrder: 'linear'
To create a more accurate quadratic mesh, use generateMesh.
gm = generateMesh(gm); gm.Mesh
ans =
FEMesh with properties:
Nodes: [3×9380 double]
Elements: [10×4732 double]
MaxElementSize: 4.9820
MinElementSize: 2.4910
MeshGradation: 1.5000
GeometricOrder: 'quadratic'
Plot the geometry with the face labels.
pdegplot(gm,FaceLabels="on",FaceAlpha=0.5);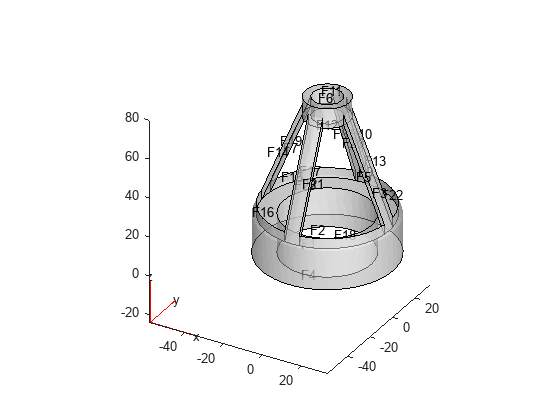
Alternatively, you can create a geometry as a DiscreteGeometry object. First, create data matrices of the appropriate sizes.
nodes = X'; elements = tet';
Then, create a PDE model and use geometryFromMesh to create a geometry from the mesh.
model = createpde; gm = geometryFromMesh(model,nodes,elements)
gm =
DiscreteGeometry with properties:
NumCells: 1
NumFaces: 23
NumEdges: 50
NumVertices: 30
Vertices: [30×3 double]
The model contains the imported linear mesh.
model.Mesh
ans =
FEMesh with properties:
Nodes: [3×1456 double]
Elements: [4×4969 double]
MaxElementSize: 8.2971
MinElementSize: 1.9044
MeshGradation: []
GeometricOrder: 'linear'
To create a more accurate quadratic mesh, use generateMesh.
generateMesh(model)
ans =
FEMesh with properties:
Nodes: [3×9380 double]
Elements: [10×4732 double]
MaxElementSize: 4.9820
MinElementSize: 2.4910
MeshGradation: 1.5000
GeometricOrder: 'quadratic'
2-D Multidomain Geometry
Create a 2-D multidomain geometry from a planar mesh.
The MultidomainMesh2D file, which is included in Partial Differential Equation Toolbox™, contains a 2-D mesh. Load information about nodes, elements, and element-to-domain correspondence into your workspace.
load MultidomainMesh2DCreate a geometry from the mesh nodes and elements.
gm = fegeometry(nodes',elements',ElementIdToRegionId);
Plot the geometry with the face labels.
pdegplot(gm,FaceLabels="on")