Heat Transfer in Block with Cavity

Create Model with Geometry

The first step in solving this heat transfer problem is to create an femodel object for thermal analysis with a geometry representing a block with a cavity.

model = femodel(AnalysisType="thermalTransient", ...
                Geometry=@crackg);

Plot Geometry

Plot the geometry with edge labels.

pdegplot(model,EdgeLabels="on");
xlim([-0.6,0.6])
ylim([-1,1])

Specify Thermal Properties of Material

Specify the thermal conductivity, mass density, and specific heat of the material.

model.MaterialProperties = ...
            materialProperties(ThermalConductivity=1, ...
                               MassDensity=1, ...
                               SpecificHeat=1);

Apply Boundary Conditions

Specify the temperature on the left edge as 100 and constant heat flow to the exterior through the right edge as –10. The toolbox uses the default insulating boundary condition for all other boundaries.

model.EdgeBC(6) = edgeBC(Temperature=100);
model.EdgeLoad(1) = edgeLoad(Heat=-10);

Set Initial Conditions

Set an initial value of 0 for the temperature.

model.FaceIC = faceIC(Temperature=0);

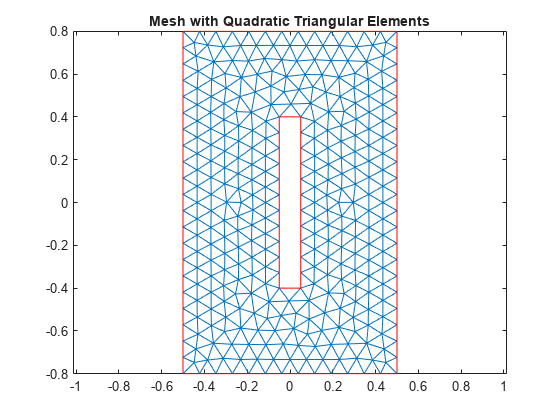
Generate Mesh

Generate a mesh and assign the result to the model. This assignment updates the mesh stored in the Geometry property of the model. Plot the mesh.

model = generateMesh(model);

figure
pdemesh(model);
title("Mesh with Quadratic Triangular Elements")

Specify Solution Times

Set solution times to be 0 to 5 seconds in steps of 1/2.

tlist = 0:0.5:5;

Calculate Solution

Calculate the solution by using the solve function.

results = solve(model,tlist)

results = 
  TransientThermalResults with properties:

      Temperature: [1308x11 double]
    SolutionTimes: [0 0.5000 1 1.5000 2 2.5000 3 3.5000 4 4.5000 5]
       XGradients: [1308x11 double]
       YGradients: [1308x11 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Evaluate Heat Flux

Compute the heat flux density.

[qx,qy] = evaluateHeatFlux(results);

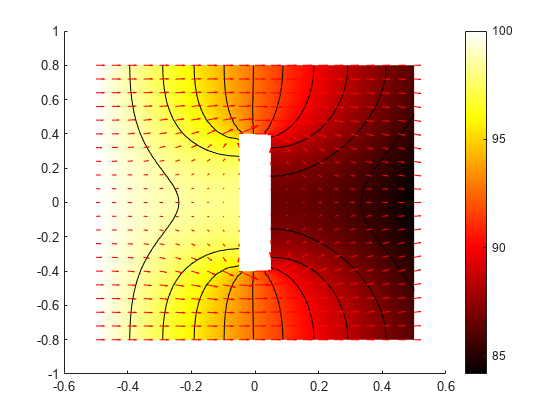
Plot Temperature Distribution and Heat Flux

Plot the solution at the final time step, t = 5.0 seconds, with isothermal lines using a contour plot, and plot the heat flux vector field using arrows.

figure
pdeplot(results.Mesh,XYData=results.Temperature(:,end), ...
                     Contour="on",...
                     FlowData=[qx(:,end),qy(:,end)], ...
                     ColorMap="hot")