Main Content

Inhomogeneous Heat Equation on Square Domain

Open Live Script

This example shows how to solve the heat equation with a source term.

The basic heat equation with a unit source term is

∂u∂t-Δu=1

This equation is solved on a square domain with a discontinuous initial condition and zero temperatures on the boundaries.

Create a square geometry centered at x = 0 and y = 0 with sides of length 2. Include a circle of radius 0.4 concentric with the square.

R1 = [3;4;-1;1;1;-1;-1;-1;1;1];
C1 = [1;0;0;0.4];
C1 = [C1;zeros(length(R1) - length(C1),1)];
gd = [R1,C1];
sf = 'R1+C1';
ns = char('R1','C1')';
g = decsg(gd,sf,ns);

Plot the geometry with edge and face labels.

figure
pdegplot(g,EdgeLabels="on",FaceLabels="on")
axis([-1.1 1.1 -1.1 1.1]);
axis equal

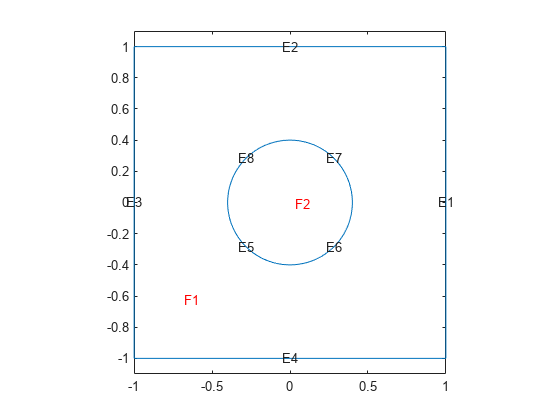
Figure contains an axes object. The axes object contains 11 objects of type line, text.

Create an femodel object for transient thermal analysis and include the geometry.

model = femodel(AnalysisType="thermalTransient", ...
                Geometry=g);

Specify thermal properties of the material.

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=1,...
                       MassDensity=1,...
                       SpecificHeat=1);

Specify internal heat source.

model.FaceLoad = faceLoad(Heat=1);

Set zero temperatures on all four outer edges of the square.

model.EdgeBC(1:4) = edgeBC(Temperature=0);

The discontinuous initial value is 1 inside the circle and zero outside. Specify zero initial temperature everywhere.

model.FaceIC = faceIC(Temperature=0);

Specify nonzero initial temperature inside the circle (Face 2).

model.FaceIC(2) = faceIC(Temperature=1);

Generate and plot a mesh.

model = generateMesh(model);
figure;
pdemesh(model); 
axis equal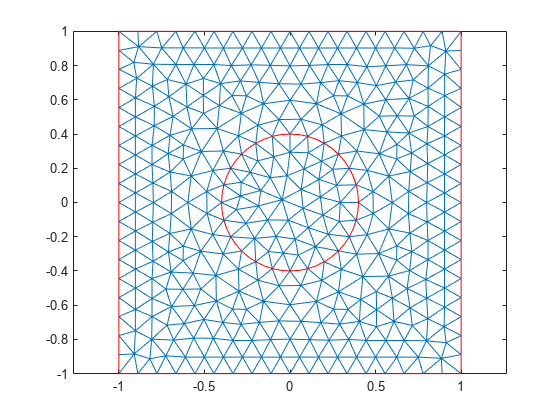

Figure contains an axes object. The axes object contains 2 objects of type line.

Find the solution at 20 points in time between 0 and 0.1.

nframes = 20;
tlist = linspace(0,0.1,nframes);

model.SolverOptions.ReportStatistics ='on';
result = solve(model,tlist);
T = result.Temperature;

Plot the solution.

figure
Tmax = max(max(T));
Tmin = min(min(T));
for j = 1:nframes
    pdeplot(result.Mesh,XYData=T(:,j),ZData=T(:,j));
    axis([-1 1 -1 1 0 1]);
    Mv(j) = getframe;
end

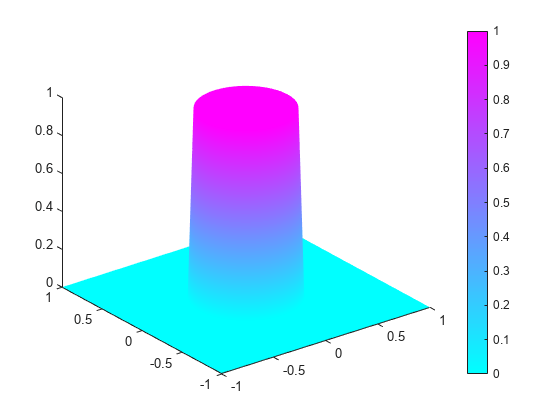
Figure contains an axes object. The axes object contains an object of type patch.

To play the animation, use the movie(Mv,1) command.