ModalThermalResults

Modal thermal solution

Since R2022a

expand all in page

Description

A ModalThermalResults object contains the eigenvalues and eigenvector matrix of a thermal analysis problem, and average of snapshots used for proper orthogonal decomposition (POD).

Creation

Solve a modal thermal problem using the solve function. This function returns a modal thermal solution as a ModalThermalResults object.

Properties

expand all

This property is read-only.

Eigenvalues of a thermal problem, returned as a column vector.

Data Types: double

This property is read-only.

Eigenvector matrix, returned as a matrix.

Data Types: double

This property is read-only.

Average of snapshots used for POD, returned as a column vector.

Data Types: double

This property is read-only.

Type of modes, returned as "EigenModes" or "PODModes".

Data Types: string

This property is read-only.

Finite element mesh, returned as an FEMesh object.

Examples

collapse all

Open Live Script

Solve a transient thermal problem by first obtaining mode shapes for a particular decay range and then using the modal superposition method.

Modal Decomposition

Create a geometry representing a square plate with a diamond-shaped region in its center.

SQ1 = [3; 4; 0; 3; 3; 0; 0; 0; 3; 3];
D1 = [2; 4; 0.5; 1.5; 2.5; 1.5; 1.5; 0.5; 1.5; 2.5];
gd = [SQ1 D1];
sf = 'SQ1+D1';
ns = char('SQ1','D1');
ns = ns';
g = decsg(gd,sf,ns);
pdegplot(g,EdgeLabels="on",FaceLabels="on")
xlim([-1.5 4.5])
ylim([-0.5 3.5])
axis equal

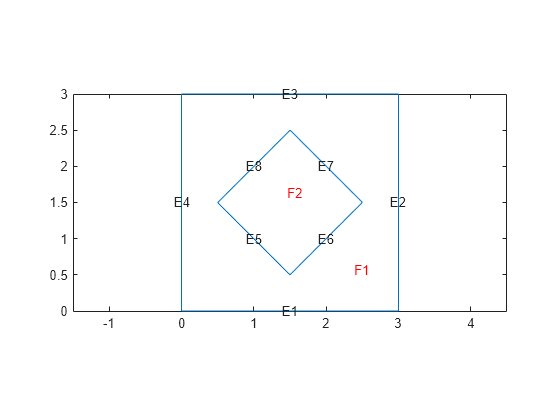
Figure contains an axes object. The axes object contains 11 objects of type line, text.

Create an femodel object for modal thermal analysis and include the geometry.

model = femodel(AnalysisType="thermalModal", ...
                Geometry=g);

For the square region, assign these thermal properties:

  • Thermal conductivity is 10 W/(m⋅∘C).

  • Mass density is 2 kg/m3.

  • Specific heat is 0.1 J/(kg⋅∘C).

model.MaterialProperties(1) = ...
    materialProperties(ThermalConductivity=10, ...
                       MassDensity=2, ...
                       SpecificHeat=0.1);

For the diamond region, assign these thermal properties:

  • Thermal conductivity is 2 W/(m⋅∘C).

  • Mass density is 1 kg/m3.

  • Specific heat is 0.1 J/(kg⋅∘C).

model.MaterialProperties(2) = ...
    materialProperties(ThermalConductivity=2, ...
                       MassDensity=1, ...
                       SpecificHeat=0.1);

Assume that the diamond-shaped region is a heat source with a density of 4 W/m2.

model.FaceLoad(2) = faceLoad(Heat=4);

Apply a constant temperature of 0 °C to the sides of the square plate.

model.EdgeBC(1:4) = edgeBC(Temperature=0);

Set the initial temperature to 0 °C.

model.FaceIC = faceIC(Temperature=0);

Generate the mesh.

model = generateMesh(model);

Compute eigenmodes of the model in the decay range [100,10000] s-1.

RModal = solve(model,DecayRange=[100,10000])
RModal = 
  ModalThermalResults with properties:

    DecayRates: [164×1 double]
    ModeShapes: [1461×164 double]
      ModeType: "EigenModes"
          Mesh: [1×1 FEMesh]

Transient Analysis

Knowing the mode shapes, you can now use the modal superposition method to solve the transient thermal problem. First, switch the model analysis type to thermal transient.

model.AnalysisType = "thermalTransient";

The dynamics for this problem are very fast. The temperature reaches a steady state in about 0.1 second. To capture the most active part of the dynamics, set the solution time to logspace(-2,-1,100). This command returns 100 logarithmically spaced solution times between 0.01 and 0.1.

tlist = logspace(-2,-1,10);

Solve the equation.

Rtransient = solve(model,tlist,ModalResults=RModal);

Plot the solution with isothermal lines by using a contour plot.

msh = Rtransient.Mesh
msh = 
  FEMesh with properties:

             Nodes: [2×1461 double]
          Elements: [6×694 double]
    MaxElementSize: 0.1697
    MinElementSize: 0.0849
     MeshGradation: 1.5000
    GeometricOrder: 'quadratic'


T = Rtransient.Temperature;
pdeplot(msh,XYData=T(:,end),Contour="on", ...
                            ColorMap="hot")
axis equal

Figure contains an axes object. The axes object contains 12 objects of type patch, line.

Open Live Script

Obtain POD modes of a linear thermal problem using several instances of the transient solution (snapshots).

Create an femodel object for transient thermal analysis and include a unit square geometry in the model.

model = femodel(AnalysisType="thermalTransient", ...
                Geometry=@squareg);

Plot the geometry, displaying edge labels.

pdegplot(model.Geometry,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])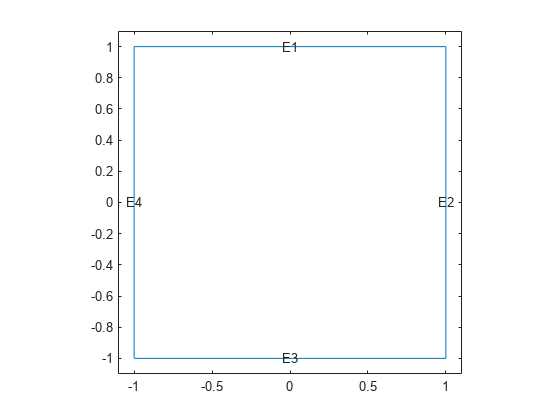

Figure contains an axes object. The axes object contains 5 objects of type line, text.

Specify the thermal conductivity, mass density, and specific heat of the material.

model.MaterialProperties = ...
    materialProperties(ThermalConductivity=400, ...
                       MassDensity=1300, ...
                       SpecificHeat=600);

Set the temperature on the right edge to 100.

model.EdgeBC(2) = edgeBC(Temperature=100);

Set an initial value of 0 for the temperature.

model.FaceIC = faceIC(Temperature=0);

Generate a mesh.

model = generateMesh(model);

Solve the model for three different values of heat source and collect snapshots. 

tlist = 0:10:600;
snapShotIDs = [1:10 59 60 61];
Tmatrix = [];

heatVariation = [10000 15000 20000];
for q = heatVariation
    model.FaceLoad = faceLoad(Heat=q);
    results = solve(model,tlist);
    Tmatrix = [Tmatrix,results.Temperature(:,snapShotIDs)];
end

Switch the model analysis type to thermal modal.

model.AnalysisType = "thermalModal";

Compute the POD modes.

RModal = solve(model,Snapshots=Tmatrix)
RModal = 
  ModalThermalResults with properties:

          DecayRates: [6×1 double]
          ModeShapes: [1529×6 double]
    SnapshotsAverage: [1529×1 double]
            ModeType: "PODModes"
                Mesh: [1×1 FEMesh]

Version History

Introduced in R2022a

See Also

Functions

Objects