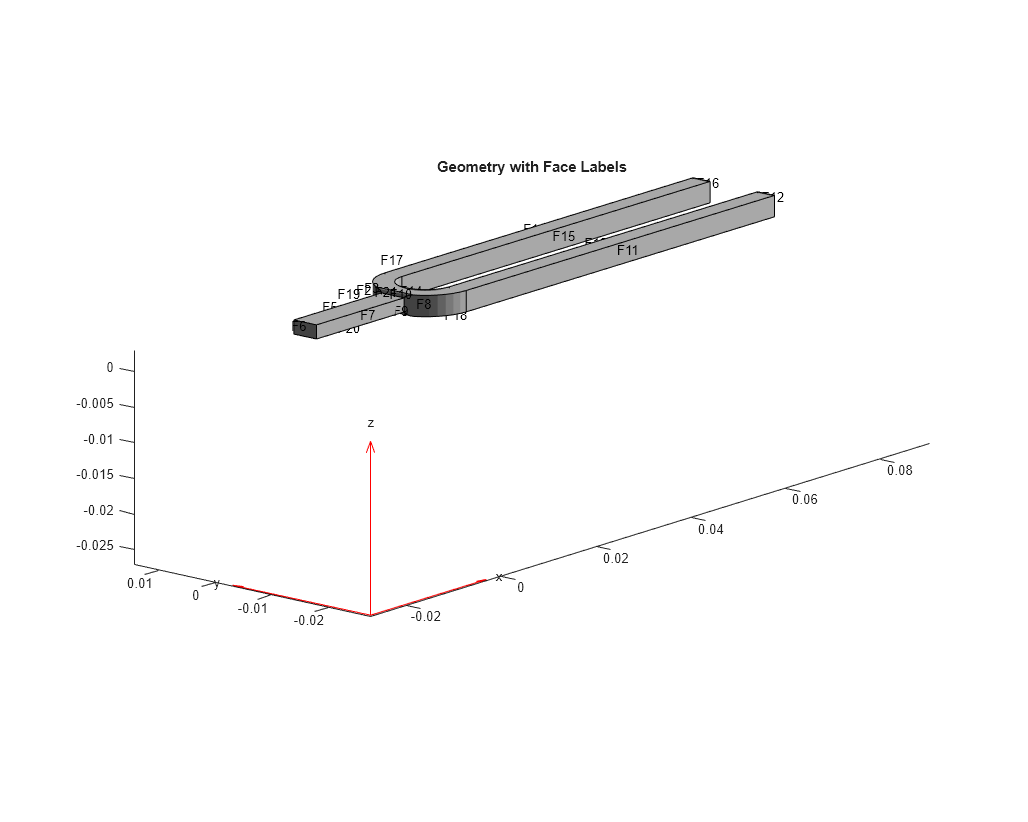
solve
Solve structural analysis, heat transfer, or electromagnetic analysis problem
Syntax
Description
results = solve(fem,"FrequencyRange",[omega1,omega2])fem for all modes in the frequency range
[omega1,omega2]. Define omega1 as
slightly lower than the lowest expected frequency and omega2
as slightly higher than the highest expected frequency. For example, if the
lowest expected frequency is zero, then use a small negative value for
omega1.
results = solve(fem,"DecayRange",[lambda1,lambda2])fem for all modes in the
decay range [lambda1,lambda2]. The resulting modes enable
you to:
Use the modal superposition method to speed up a transient thermal analysis.
Extract the reduced modal system to use, for example, in Simulink®.
results = solve(fem,"Snapshots",Tmatrix)fem using proper
orthogonal decomposition (POD). You can use the resulting modes to speed up a
transient thermal analysis or, if your thermal model is linear, to extract the
reduced modal system.
results = solve(fem,tlist,"ModalResults",thermalModalR)results = solve(fem,tlist,"ModalResults",structuralModalR)results = solve(fem,flist,"ModalResults",structuralModalR)
results = solve(fem,tlist,"ModalResults",structuralModalR,"DampingZeta",z)results = solve(fem,flist,"ModalResults",structuralModalR,"DampingZeta",z)z is the modal
damping ratio.
structuralStaticResults = solve(structuralStatic)structuralStatic.
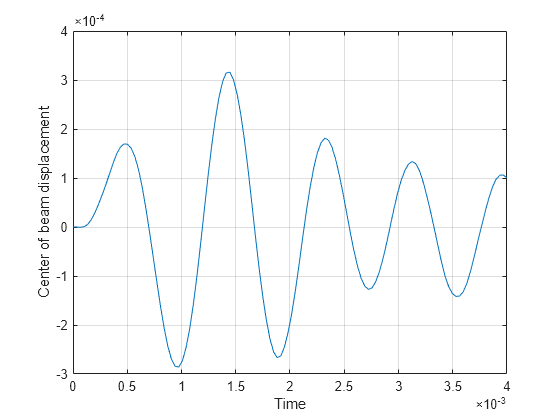
structuralTransientResults = solve(structuralTransient,tlist)structuralTransient at the times specified in
tlist.
structuralFrequencyResponseResults = solve(structuralFrequencyResponse,flist)structuralFrequencyResponse at the frequencies
specified in flist.
structuralModalResults = solve(structuralModal,"FrequencyRange",[omega1,omega2])[omega1,omega2]. Define omega1 as
slightly lower than the lowest expected frequency and omega2
as slightly higher than the highest expected frequency. For example, if the
lowest expected frequency is zero, then use a small negative value for
omega1.
structuralTransientResults = solve(structuralTransient,tlist,"ModalResults",structuralModalR)structuralFrequencyResponseResults = solve(structuralFrequencyResponse,flist,"ModalResults",structuralModalR)
thermalSteadyStateResults = solve(thermalSteadyState)thermalSteadyState.
thermalTransientResults = solve(thermalTransient,tlist)thermalTransient at the times specified in
tlist.
thermalModalResults = solve(thermalModal,"DecayRange",[lambda1,lambda2])thermalModal for all modes in the decay range
[lambda1,lambda2]. The resulting modes enable you
to:
Use the modal superposition method to speed up a transient thermal analysis.
Extract the reduced modal system to use, for example, in Simulink.
thermalModalResults = solve(thermalModal,"Snapshots",Tmatrix)
thermalTransientResults = solve(thermalTransient,tlist,"ModalResults",thermalModalR)
emagStaticResults = solve(emagmodel)emagmodel.
emagHarmonicResults = solve(emagmodel,"Frequency",omega)emagmodel at the frequencies specified in
omega.
Examples
Input Arguments
Output Arguments
Tips
When you use modal analysis results to solve a transient structural dynamics model, the
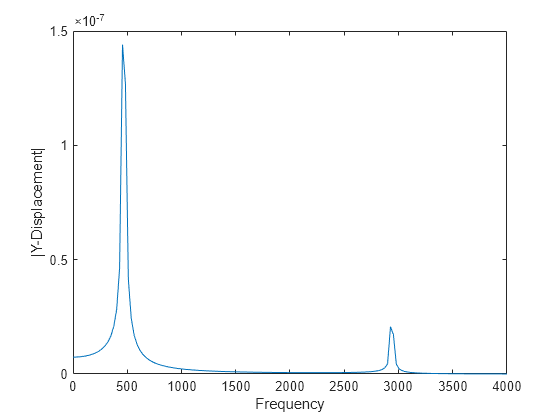
modalresultsargument must be created in Partial Differential Equation Toolbox™ from R2019a or newer.For a frequency response model with damping, the results are complex. Use functions such as
absandangleto obtain real-valued results, such as the magnitude and phase.