Main Content

step

System object: phased.IntensityScope
Namespace: phased

Update intensity scope display

expand all in page

Syntax

step(sIS,data)

Description

Note

Starting in R2016b, instead of using the step method to perform the operation defined by the System object™, you can call the object with arguments, as if it were a function. For example, y = step(obj,x) and y = obj(x) perform equivalent operations.

step(sIS,data) updates the intensity scope display with new scan lines from a real signal, data.

Note

The object performs an initialization the first time the object is executed. This initialization locks nontunable properties and input specifications, such as dimensions, complexity, and data type of the input data. If you change a nontunable property or an input specification, the System object issues an error. To change nontunable properties or inputs, you must first call the release method to unlock the object.

Input Arguments

expand all

Intensity scope display, specified as a phased.IntensityScope System object.

Example: phased.IntensityScope

Displayed intensity values, specified as a real-valued N-by-M matrix. The quantity N specifies the number of intensity bins in data. The quantity M specifies the number of intensity vectors in the data. Each column of the matrix creates a display line. Units are arbitrary. Specify the time interval between intensity vectors using the TimeResolution property.

Example: [5.0;5.1;5.0;4.9]

Data Types: double

Examples

expand all

Open Script

Use the phased.IntensityScope System object™ to display the intensities of the echoes of three moving targets as functions of range and time.

Create the Radar and Target System Objects

Set up the initial positions and velocities of the three targets. Use the phased.Platform System object to model radar and target motions. The radar is stationary while the targets undergo constant velocity motion. The simulation runs for 500 steps at 0.1 second increments, giving a total simulation time of 50 seconds.

nsteps = 500;
dt = .1;
timespan = nsteps*dt;
x1 = [60,0,0]';
x2 = [60,-80,40]';
x3 = [300,0,-300]';
v1 = [2,0,0]';
v2 = [10,5,6]';
v3 = [-10,2,-4]';
platform = phased.Platform([0,0,0]',[0,0,0]');
targets = phased.Platform([x1,x2,x3],[v1,v2,v3]);

Set Up Range Bins

Each echo is put into a range bin. The range bin resolution is 1 meter and the range is from 50 to 1000 meters.

rngres = 1.0;
rngmin = 50.0;
rngmax = 1000.0;
rngscan = [rngmin:rngres:rngmax];

Create the Gain Function

Define a range-dependent gain function to enhance the display of targets at larger ranges. The gain function amplifies the returned echo for visualization purposes only.

rangegain = @(rng)(1e12*rng^4);

Create the Intensity Scope

Set up the Intensity Scope using these properties.

  • Use the XResolution property to set the width of each scan line bin to the range resolution of 1 km.

  • Use the XOffset property to set the value of the lowest range bin to the minimum range of 50 km.

  • Use the TimeResolution property to set the value of the scan line time difference to 0.1 s.

  • Use the TimeSpan property to set the height of the display window to the time duration of the simulation.

  • Use the IntensityUnits property to set the display units to Watts.

scope = phased.IntensityScope('Name','IntensityScope Display',...
    'Title','Ranges vs. Time','XLabel','Range (m)','XResolution',rngres,...
    'XOffset',rngmin,'TimeResolution',dt,'TimeSpan',timespan, ...
    'IntensityUnits','Watts','Position',[100,100,800,450]);

Run Simulation Loop

  1. In this loop, move the targets at constant velocity using the step method of the phased.Platform System object.

  2. Compute the target ranges using the rangeangle function.

  3. Compute the target range bins by quantizing the range values in integer multiples of rngres.

  4. Fill each target range bin and neighboring bins with a simulated radar intensity value.

  5. Add the signal from each target to the scan line.

  6. Call the step method of the phased.IntensityScope System object to display the scan lines.

for k = 1:nsteps
    xradar = platform(dt);
    xtgts = targets(dt);
    [rngs] = rangeangle(xtgts,xradar);
    scanline = zeros(size(rngscan));

    rngindx = ceil((rngs(1) - rngmin)/rngres);
    scanline(rngindx + [-1:1]) = rangegain(rngs(1))/(rngs(1)^4);

    rngindx = ceil((rngs(2) - rngmin)/rngres);
    scanline(rngindx + [-1:1]) = rangegain(rngs(2))/(rngs(2)^4);

    rngindx = ceil((rngs(3) - rngmin)/rngres);
    scanline(rngindx + [-1:1]) = rangegain(rngs(3))/(rngs(3)^4);

    scope(scanline.');
    pause(.1);
end

Open Script

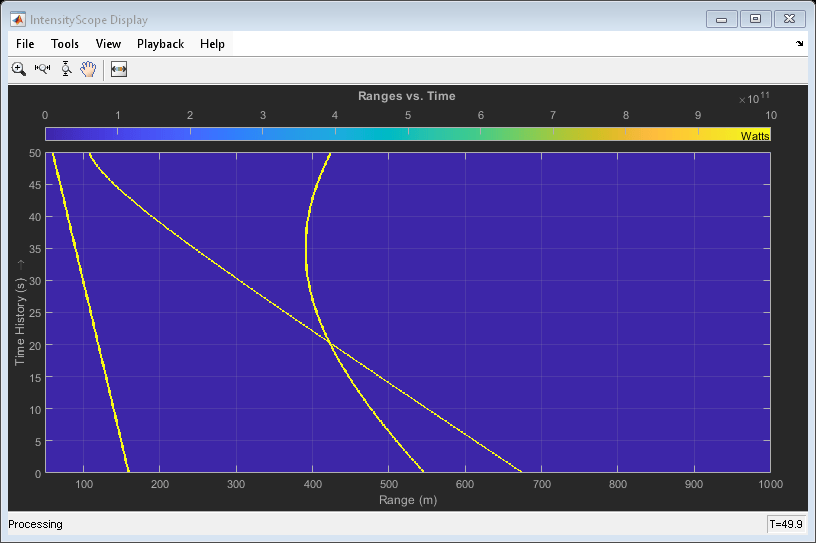
Use the phased.IntensityScope System Object™ to display the detection output of a radar system simulation. The radar scenario contains a stationary single-element monostatic radar and three moving targets.

Set Radar Operating Parameters

Set the maximum range, peak power range resolution, operating frequency, transmitter gain, and target radar cross-section.

max_range = 5000;
range_res = 50;
fc = 10e9;
tx_gain = 20;
peak_power = 5500.0;

Choose the signal propagation speed to be the speed of light, and compute the signal wavelength corresponding to the operating frequency.

c = physconst('LightSpeed');
lambda = c/fc;

Compute the pulse bandwidth from the range resolution. Set the sampling rate, fs, to twice the pulse bandwidth. The noise bandwidth is also set to the pulse bandwidth. The radar integrates a number of pulses set by num_pulse_int. The duration of each pulse is the inverse of the pulse bandwidth.

pulse_bw = c/(2*range_res);
pulse_length = 1/pulse_bw;
fs = 2*pulse_bw;
noise_bw = pulse_bw;
num_pulse_int = 10;

Set the pulse repetition frequency to match the maximum range of the radar.

prf = c/(2*max_range);

Create System Objects for the Model

Choose a rectangular waveform.

waveform = phased.RectangularWaveform('PulseWidth',pulse_length,...
    'PRF',prf,'SampleRate',fs);

Set the receiver amplifier characteristics.

amplifier = phased.ReceiverPreamp('Gain',20,'NoiseFigure',0,...
    'SampleRate',fs,'EnableInputPort',true,'SeedSource','Property',...
    'Seed',2007);
transmitter = phased.Transmitter('Gain',tx_gain,'PeakPower',peak_power,...
    'InUseOutputPort',true);

Specify the radar antenna as a single isotropic antenna.

antenna = phased.IsotropicAntennaElement('FrequencyRange',[5e9 15e9]);

Set up a monostatic radar platform.

radarplatform = phased.Platform('InitialPosition',[0; 0; 0],...
    'Velocity',[0; 0; 0]);

Set up the three target platforms using a single System object.

targetplatforms = phased.Platform(...
    'InitialPosition',[2000.66 3532.63 3845.04; 0 0 0; 0 0 0], ...
    'Velocity',[150 -150 0; 0 0 0; 0 0 0]);

Create the radiator and collector System objects.

radiator = phased.Radiator('Sensor',antenna,'OperatingFrequency',fc);
collector = phased.Collector('Sensor',antenna,'OperatingFrequency',fc);

Set up the three target RCS properties.

targets = phased.RadarTarget('MeanRCS',[1.6 2.2 1.05],'OperatingFrequency',fc);

Create System object to model two-way freespace propagation.

channels= phased.FreeSpace('SampleRate',fs,'TwoWayPropagation',true,...
    'OperatingFrequency',fc);

Define a matched filter.

MFcoef = getMatchedFilter(waveform);
mfilter = phased.MatchedFilter('Coefficients',MFcoef,'GainOutputPort',true);

Create Range and Doppler Bins

Set up the fast-time grid. Fast time is the sampling time of the echoed pulse relative to the pulse transmission time. The range bins are the ranges corresponding to each bin of the fast time grid.

fast_time = unigrid(0,1/fs,1/prf,'[)');
range_bins = c*fast_time/2;

To compensate for range loss, create a time varying gain System Object.

gain = phased.TimeVaryingGain('RangeLoss',2*fspl(range_bins,lambda),...
    'ReferenceLoss',2*fspl(max_range,lambda));

Set up Doppler bins. Doppler bins are determined by the pulse repetition frequency. Create an FFT System object for Doppler processing.

DopplerFFTbins = 32;
DopplerRes = prf/DopplerFFTbins;
fft = dsp.FFT('FFTLengthSource','Property',...
    'FFTLength',DopplerFFTbins);

Create Data Cube

Set up a reduced data cube. Normally, a data cube has fast-time and slow-time dimensions and the number of sensors. Because the data cube has only one sensor, it is two-dimensional.

rx_pulses = zeros(numel(fast_time),num_pulse_int);

Create IntensityScope System Objects

Create two IntensityScope System objects, one for Doppler-time-intensity and the other for range-time-intensity.

dtiscope = phased.IntensityScope('Name','Doppler-Time Display',...
    'XLabel','Velocity (m/sec)', ...
    'XResolution',dop2speed(DopplerRes,c/fc)/2, ...
    'XOffset',dop2speed(-prf/2,c/fc)/2,...
    'TimeResolution',0.05,'TimeSpan',5,'IntensityUnits','Mag');
rtiscope = phased.IntensityScope('Name','Range-Time Display',...
    'XLabel','Range (m)', ...
    'XResolution',c/(2*fs), ...
    'TimeResolution',0.05,'TimeSpan',5,'IntensityUnits','Mag');

Run the Simulation Loop over Multiple Radar Transmissions

Transmit 2000 pulses. Coherently process groups of 10 pulses at a time.

For each pulse:

  1. Update the radar position and velocity radarplatform

  2. Update the target positions and velocities targetplatforms

  3. Create the pulses of a single wave train to be transmitted transmitter

  4. Compute the ranges and angles of the targets with respect to the radar

  5. Radiate the signals to the targets radiator

  6. Propagate the pulses to the target and back channels

  7. Reflect the signals off the target targets

  8. Receive the signal sCollector

  9. Amplify the received signal amplifier

  10. Form data cube

For each set of 10 pulses in the data cube:

  1. Match filter each row (fast-time dimension) of the data cube.

  2. Compute the Doppler shifts for each row (slow-time dimension) of the data cube.

pri = 1/prf;
nsteps = 200;
for k = 1:nsteps
    for m = 1:num_pulse_int
        [ant_pos,ant_vel] = radarplatform(pri);
        [tgt_pos,tgt_vel] = targetplatforms(pri);
        sig = waveform();
        [s,tx_status] = transmitter(sig);
        [~,tgt_ang] = rangeangle(tgt_pos,ant_pos);
        tsig = radiator(s,tgt_ang);
        tsig = channels(tsig,ant_pos,tgt_pos,ant_vel,tgt_vel);
        rsig = targets(tsig);
        rsig = collector(rsig,tgt_ang);
        rx_pulses(:,m) = amplifier(rsig,~(tx_status>0));
    end

    rx_pulses = mfilter(rx_pulses);
    MFdelay = size(MFcoef,1) - 1;
    rx_pulses = buffer(rx_pulses((MFdelay + 1):end), size(rx_pulses,1));
    rx_pulses = gain(rx_pulses);
    range = pulsint(rx_pulses,'noncoherent');
    rtiscope(range);
    dshift = fft(rx_pulses.');
    dshift = fftshift(abs(dshift),1);
    dtiscope(mean(dshift,2));
    radarplatform(.05);
    targetplatforms(.05);
end

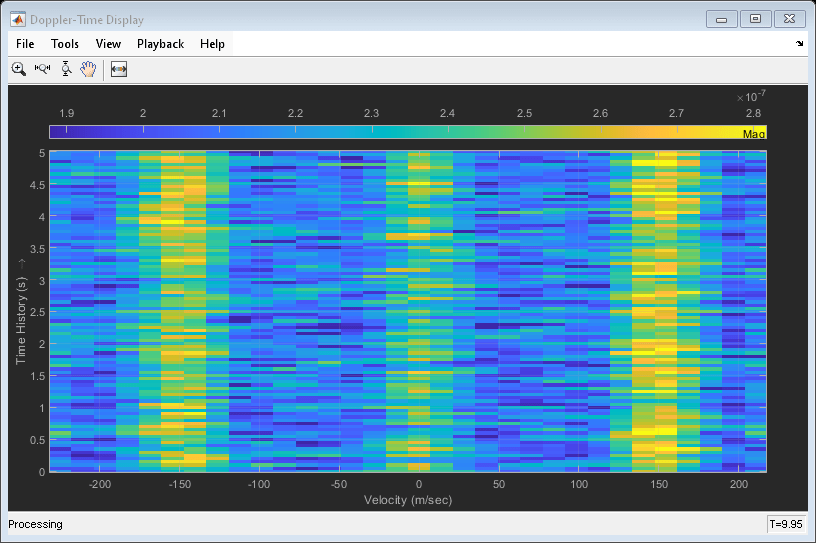
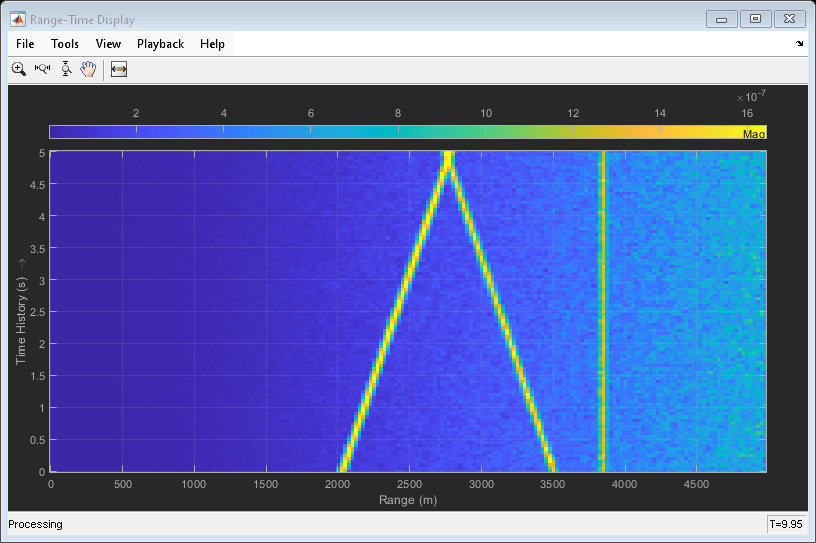
All of the targets lie on the x-axis. Two targets are moving along the x-axis and one is stationary. Because the radar is at the origin, you can read the target speed directly from the Doppler-Time Display window. The values agree with the specified velocities of -150, 150, and 0 m/sec.

Open Script

Use the phased.IntensityScope System object™ to display the angular motions of moving targets as functions of time. Each horizontal line (scan line) shows the strength of radar echoes at different azimuth angles. Azimuth space is divided into azimuth bins and each bin is filled with a simulated value depending upon the position of the targets.

Create Radar and Target System Objects

Set up the initial positions and velocities of the three targets. Use the phased.Platform System object to model radar and target motions. The radar is stationary while the targets undergo constant velocity motion. The simulation runs for 200 steps at 0.5 second intervals, giving a total simulation time of 100 seconds.

nsteps = 200;
dt = 0.5;
timespan = nsteps*dt;
x1 = [60,0,0]';
x2 = [60,-80,40]';
x3 = [300,0,-300]';
x3 = [-300,0,-300]';

v1 = [2,0,0]';
v2 = [10,5,6]';
v3 = [-10,2,-4]';
radarplatform = phased.Platform([0,0,0]',[0,0,0]');
targets = phased.Platform([x1,x2,x3],[v1,v2,v3]);

Set Up Azimuth Angle Bins

The signal for each echo is put into an angle bin and two adjacent bins. Bin resolution is 1 degree and the angle span is from −180 to 180 degrees.

angres = 1.0;
angmin = -180.0;
angmax = 180.0;
angscan = [angmin:angres:angmax];
na = length(angscan);

Range Gain Function

Define a range-dependent gain function to enhance the display of targets at larger ranges. The gain function amplifies the returned echo for visualization purposes only.

rangegain = @(rng)(1e12*rng^4);

Set Up Scope Viewer

The XResolution name-value pair specifies the width of each bin of the scan line. The XOffset sets the value of the lowest azimuth angle bin. The TimeResolution name-value pair specifies the time difference between scan lines. The TimeSpan name-value pair sets the height of the display window. A scan line is created with each call to the step method. Intensity units are amplitude units.

scope = phased.IntensityScope( ...
    'Name','IntensityScope Display',...
    'Title','Azimuth vs. Time',...
    'XLabel','Azimuth (deg)', ...
    'XResolution',angres,'XOffset',angmin,...
    'TimeResolution',dt,'TimeSpan',timespan, ...
    'IntensityUnits','Watts',...
    'Position',[100,100,800,450]);

Update-Display Loop

  1. In this loop, move the targets at constant velocity using the step method of the phased.Platform System object.

  2. Compute the target ranges and azimuth angles using the rangeangle function.

  3. Compute the azimuth angle bins by quantizing the azimuth angle values in integer multiples of angres.

  4. Fill each target azimuth bin and neighboring bins with a simulated radar intensity value.

  5. Call the phased.IntensityScope step method to display the scan line.

for k = 1:nsteps
    xradar = radarplatform(dt);
    xtgts = targets(dt);
    [rngs,angs] = rangeangle(xtgts,xradar);
    scanline = zeros(size(angscan));

    angindx = ceil((angs(1,1) - angmin)/angres) + 1;
    idx = angindx + [-1:1];
    idx(idx>na)=[];
    idx(idx<1)=[];
    scanline(idx) = rangegain(rngs(1))/(rngs(1)^4);

    angindx = ceil((angs(1,2) - angmin)/angres) + 1;
    idx = angindx + [-1:1];
    idx(idx>na)=[];
    idx(idx<1)=[];
    scanline(idx) = rangegain(rngs(2))/(rngs(2)^4);

    angindx = ceil((angs(1,3) - angmin)/angres) + 1;
    idx = angindx + [-1:1];
    idx(idx>na)=[];
    idx(idx<1)=[];
    scanline(idx) = rangegain(rngs(3))/(rngs(3)^4);
    scope(scanline.');
    pause(.1);
end

Version History

Introduced in R2016a