Acoustic Beamforming Using a Microphone Array

Define a Uniform Linear Array

First, we define a uniform linear array (ULA) to receive the signal. The array contains 10 omnidirectional microphones and the element spacing is 5 cm.

microphone = ...
    phased.OmnidirectionalMicrophoneElement('FrequencyRange',[20 20e3]);

Nele = 10;
ula = phased.ULA(Nele,0.05,'Element',microphone);
c = 340;                         % sound speed, in m/s

Simulate the Received Signals

Next, we simulate the multichannel signals received by the microphone array. We begin by loading two recorded speeches and one laughter recording. We also load the laughter audio segment as interference. The sampling frequency of the audio signals is 8 kHz.

Because the audio signal is usually large, it is often not practical to read the entire signal into the memory. Therefore, in this example, we will simulate and process the signal in a streaming fashion, i.e., breaking the signal into small blocks at the input, processing each block, and then assembling them at the output.

The incident direction of the first speech signal is -30 degrees in azimuth and 0 degrees in elevation. The direction of the second speech signal is -10 degrees in azimuth and 10 degrees in elevation. The interference comes from 20 degrees in azimuth and 0 degrees in elevation.

ang_dft = [-30; 0];
ang_cleanspeech = [-10; 10];
ang_laughter = [20; 0];

Now we can use a wideband collector to simulate a 3-second multichannel signal received by the array. Notice that this approach assumes that each input single-channel signal is received at the origin of the array by a single microphone.

fs = 8000;
collector = phased.WidebandCollector('Sensor',ula,'PropagationSpeed',c,...
    'SampleRate',fs,'NumSubbands',1000,'ModulatedInput', false);

t_duration = 3;  % 3 seconds
t = 0:1/fs:t_duration-1/fs;

We generate a white noise signal with a power of 1e-4 watts to represent the thermal noise for each sensor. A local random number stream ensures reproducible results.

prevS = rng(2008);
noisePwr = 1e-4; % noise power

We now start the simulation. At the output, the received signal is stored in a 10-column matrix. Each column of the matrix represents the signal collected by one microphone. Note that we are also playing back the audio using the streaming approach during the simulation.

% preallocate
NSampPerFrame = 1000;
NTSample = t_duration*fs;
sigArray = zeros(NTSample,Nele);
voice_dft = zeros(NTSample,1);
voice_cleanspeech = zeros(NTSample,1);
voice_laugh = zeros(NTSample,1);

% set up audio device writer
audioWriter = audioDeviceWriter('SampleRate',fs, ...
        'SupportVariableSizeInput', true);
isAudioSupported = (length(getAudioDevices(audioWriter))>1);

dftFileReader = dsp.AudioFileReader('dft_voice_8kHz.wav',...
    'SamplesPerFrame',NSampPerFrame);
speechFileReader = dsp.AudioFileReader('cleanspeech_voice_8kHz.wav',...
    'SamplesPerFrame',NSampPerFrame);
laughterFileReader = dsp.AudioFileReader('laughter_8kHz.wav',...
    'SamplesPerFrame',NSampPerFrame);

% simulate
for m = 1:NSampPerFrame:NTSample
    sig_idx = m:m+NSampPerFrame-1;
    x1 = dftFileReader();
    x2 = speechFileReader();
    x3 = 2*laughterFileReader();
    temp = collector([x1 x2 x3],...
        [ang_dft ang_cleanspeech ang_laughter]) + ...
        sqrt(noisePwr)*randn(NSampPerFrame,Nele);
    if isAudioSupported
        play(audioWriter,0.5*temp(:,3));
    end
    sigArray(sig_idx,:) = temp;
    voice_dft(sig_idx) = x1;
    voice_cleanspeech(sig_idx) = x2;
    voice_laugh(sig_idx) = x3;
end

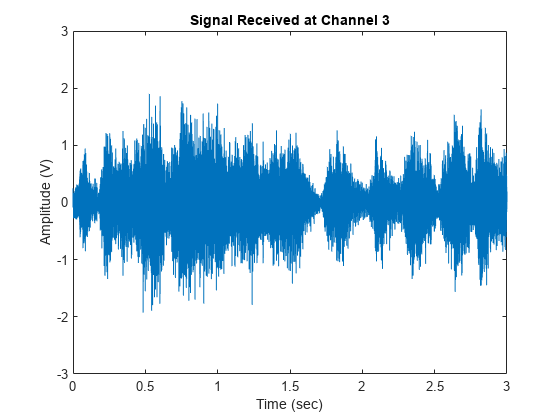
Notice that the laughter masks the speech signals, rendering them unintelligible. We can plot the signal in channel 3 as follows:

plot(t,sigArray(:,3));
xlabel('Time (sec)'); ylabel ('Amplitude (V)');
title('Signal Received at Channel 3'); ylim([-3 3]);

Process with a Time Delay Beamformer

The time delay beamformer compensates for the arrival time differences across the array for a signal coming from a specific direction. The time aligned multichannel signals are coherently averaged to improve the signal-to-noise ratio (SNR). Now, define a steering angle corresponding to the incident direction of the first speech signal and construct a time delay beamformer.

angSteer = ang_dft;
beamformer = phased.TimeDelayBeamformer('SensorArray',ula,...
    'SampleRate',fs,'Direction',angSteer,'PropagationSpeed',c)

beamformer = 
  phased.TimeDelayBeamformer with properties:

          SensorArray: [1x1 phased.ULA]
     PropagationSpeed: 340
           SampleRate: 8000
      DirectionSource: 'Property'
            Direction: [2x1 double]
    WeightsOutputPort: false

Next, we process the synthesized signal, plot and listen to the output of the conventional beamformer. Again, we play back the beamformed audio signal during the processing.

signalsource = dsp.SignalSource('Signal',sigArray,...
    'SamplesPerFrame',NSampPerFrame);

cbfOut = zeros(NTSample,1);

for m = 1:NSampPerFrame:NTSample
    temp = beamformer(signalsource());
    if isAudioSupported
        play(audioWriter,temp);
    end
    cbfOut(m:m+NSampPerFrame-1,:) = temp;
end

plot(t,cbfOut);
xlabel('Time (Sec)'); ylabel ('Amplitude (V)');
title('Time Delay Beamformer Output'); ylim([-3 3]);

One can measure the speech enhancement by the array gain, which is the ratio of output signal-to-interference-plus-noise ratio (SINR) to input SINR.

agCbf = pow2db(mean((voice_cleanspeech+voice_laugh).^2+noisePwr)/...
    mean((cbfOut - voice_dft).^2))

agCbf = 
9.5022

The first speech signal begins to emerge in the time delay beamformer output. We obtain an SINR improvement of 9.4 dB. However, the background laughter is still comparable to the speech. To obtain better beamformer performance, use a Frost beamformer.

Process with a Frost Beamformer

By attaching FIR filters to each sensor, the Frost beamformer has more beamforming weights to suppress the interference. It is an adaptive algorithm that places nulls at learned interference directions to better suppress the interference. In the steering direction, the Frost beamformer uses distortionless constraints to ensure desired signals are not suppressed. Let us create a Frost beamformer with a 20-tap FIR after each sensor.

frostbeamformer = ...
    phased.FrostBeamformer('SensorArray',ula,'SampleRate',fs,...
    'PropagationSpeed',c,'FilterLength',20,'DirectionSource','Input port');

Next, process the synthesized signal using the Frost beamformer.

reset(signalsource);
FrostOut = zeros(NTSample,1);
for m = 1:NSampPerFrame:NTSample
    FrostOut(m:m+NSampPerFrame-1,:) = ...
        frostbeamformer(signalsource(),ang_dft);
end

We can play and plot the entire audio signal once it is processed.

if isAudioSupported
    play(audioWriter,FrostOut);
end

plot(t,FrostOut);
xlabel('Time (sec)'); ylabel ('Amplitude (V)');
title('Frost Beamformer Output'); ylim([-3 3]);

% Calculate the array gain
agFrost = pow2db(mean((voice_cleanspeech+voice_laugh).^2+noisePwr)/...
    mean((FrostOut - voice_dft).^2))

agFrost = 
14.4385

Notice that the interference is now canceled. The Frost beamformer has an array gain of 14 dB, which is 4.5 dB higher than that of the time delay beamformer. The performance improvement is impressive, but has a high computational cost. In the preceding example, an FIR filter of order 20 is used for each microphone. With all 10 sensors, one needs to invert a 200-by-200 matrix, which may be expensive in real-time processing.

Use Diagonal Loading to Improve Robustness of the Frost Beamformer

Next, we want to steer the array in the direction of the second speech signal. Suppose we do not know the exact direction of the second speech signal except a rough estimate of azimuth -5 degrees and elevation 5 degrees.

release(frostbeamformer);
ang_cleanspeech_est = [-5; 5];  % Estimated steering direction

reset(signalsource);
FrostOut2 = zeros(NTSample,1);
for m = 1:NSampPerFrame:NTSample
    FrostOut2(m:m+NSampPerFrame-1,:) = frostbeamformer(signalsource(),...
        ang_cleanspeech_est);
end

if isAudioSupported
    play(audioWriter,FrostOut2);
end

plot(t,FrostOut2);
xlabel('Time (sec)'); ylabel ('Amplitude (V)');
title('Frost Beamformer Output');  ylim([-3 3]);

% Calculate the array gain
agFrost2 = pow2db(mean((voice_dft+voice_laugh).^2+noisePwr)/...
    mean((FrostOut2 - voice_cleanspeech).^2))

agFrost2 = 
6.1927

The speech is barely audible. Despite the 6.1 dB gain from the beamformer, performance suffers from the inaccurate steering direction. One way to improve the robustness of the Frost beamformer is to use diagonal loading. This approach adds a small quantity to the diagonal elements of the estimated covariance matrix. Here we use a diagonal value of 1e-3.

% Specify diagonal loading value
release(frostbeamformer);
frostbeamformer.DiagonalLoadingFactor = 1e-3;

reset(signalsource);
FrostOut2_dl = zeros(NTSample,1);
for m = 1:NSampPerFrame:NTSample
    FrostOut2_dl(m:m+NSampPerFrame-1,:) = ...
        frostbeamformer(signalsource(),ang_cleanspeech_est);
end

if isAudioSupported
    play(audioWriter,FrostOut2_dl);
end

plot(t,FrostOut2_dl);
xlabel('Time (sec)'); ylabel ('Amplitude (V)');
title('Frost Beamformer Output');  ylim([-3 3]);

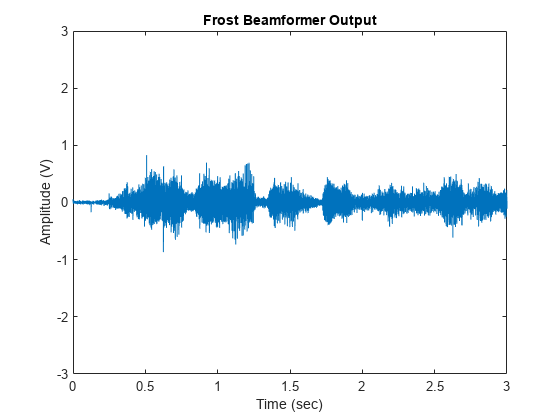
% Calculate the array gain
agFrost2_dl = pow2db(mean((voice_dft+voice_laugh).^2+noisePwr)/...
    mean((FrostOut2_dl - voice_cleanspeech).^2))

agFrost2_dl = 
6.4788

Now the output speech signal is improved and we obtain a 0.3 dB gain improvement from the diagonal loading technique.

release(frostbeamformer);
release(signalsource);
if isAudioSupported
    pause(3); % flush out AudioPlayer buffer
    release(audioWriter);
end
rng(prevS);

Summary

This example shows how to use time domain beamformers to retrieve speech signals from noisy microphone array measurements. The example also shows how to simulate an interference-dominant signal received by a microphone array. The example used both time delay and the Frost beamformers and compared their performance. The Frost beamformer has a better interference suppression capability. The example also illustrates the use of diagonal loading to improve the robustness of the Frost beamformer.

Reference

[1] O. L. Frost III, An algorithm for linear constrained adaptive array processing, Proceedings of the IEEE, Vol. 60, Number 8, Aug. 1972, pp. 925-935.