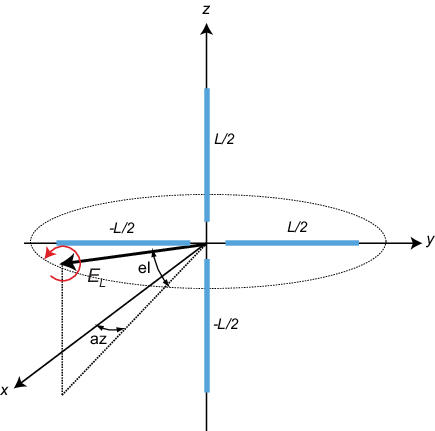
Crossed-dipole Antenna Element
Another antenna that produces polarized radiation is the crossed-dipole
antenna, created by using the phased.CrossedDipoleAntennaElement System object™.
You can use a cross-dipole antenna to generate circularly-polarized radiation. The crossed-dipole antenna consists of two identical but orthogonal short-dipole antennas that are phased 90° apart. A diagram of the crossed dipole antenna appears in the following figure. The electric field created by a crossed-dipole antenna constructed from a y-directed short dipole and a z-directed short dipole has the form
The polarization ratio EV/EH, when evaluated along the x-axis, is just –i which means that the polarization is exactly RHCP along the x-axis. It is predominantly RHCP when the observation point is close to the x-axis. Moving away from the x-axis, the field becomes a mixture of LHCP and RHCP polarizations. Along the –x-axis, the field is LHCP polarized. The figure illustrates, for a point near the x, that the field is primarily RHCP.
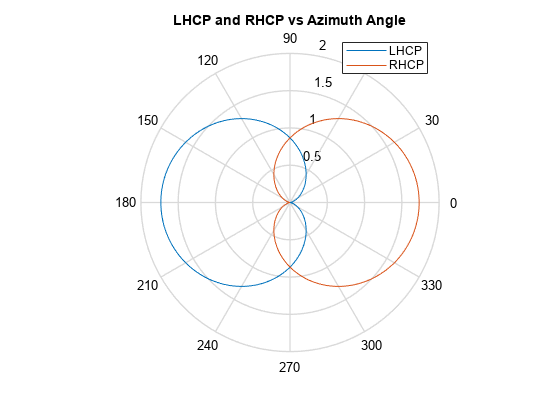
LHCP and RHCP Polarization Components
This example plots the right-hand and left-hand circular polarization components of fields generated by a crossed-dipole antenna at 1.5 GHz. You can see how the circular polarization changes from pure RHCP at 0 degrees azimuth angle to pure LHCP at 180 degrees azimuth angle, both at 0 degrees elevation angle.
Create the phased.CrossedDipoleAntennaElement object.
fc = 1.5e9;
antenna = phased.CrossedDipoleAntennaElement('FrequencyRange',[1,2]*1e9);Compute the left-handed and right-handed circular polarization components from the antenna response.
az = [-180:180]; el = zeros(size(az)); resp = antenna(fc,[az;el]); cfv = pol2circpol([resp.H.';resp.V.']); clhp = cfv(1,:); crhp = cfv(2,:);
Plot both circular polarization components at 0 degrees elevation.
polar(az*pi/180.0,abs(clhp)) hold on polar(az*pi/180.0,abs(crhp)) title('LHCP and RHCP vs Azimuth Angle') legend('LHCP','RHCP') hold off