Improve SNR and Capacity of Wireless Communication Using Antenna Arrays
The goal of a wireless communication system is to serve as many users with the highest possible data rate given constraints such as radiation power limit and operating budget. To improve the data rate, the key is to improve the signal to noise ratio (SNR). To serve more users, the key is to reuse the resources. Over the last several decades, numerous algorithms have been adopted to improve the SNR and reuse the resources in time, frequency, and coding spaces. This example shows how the adoption of antenna arrays can help improve the SNR and capacity of a wireless link.
Introduction
Antenna arrays have become part of the standard configuration in 5G wireless communication systems. Because there are multiple elements in an antenna array, such wireless communications systems are often referred to as multiple input multiple output (MIMO) systems. Antenna arrays can help improve the SNR by exploring the redundancy across the multiple transmit and receive channels. They also make it possible to reuse the spatial information in the system to improve the coverage.
For this example, assume the system is deployed at 60 GHz, which is a frequency being considered for the 5G system.
c = 3e8; % propagation speed fc = 60e9; % carrier frequency lambda = c/fc; % wavelength rng(6466);
With no loss in generality, place the transmitter at the origin and place the receiver approximately 1.6 km away.
txcenter = [0;0;0]; rxcenter = [1500;500;0];
Throughout this example, the scatteringchanmtx function will be used to create a channel matrix for different transmit and receive array configurations. The function simulates multiple scatterers between the transmit and receive arrays. The signal travels from the transmit array to all the scatterers first and then bounces off the scatterers and arrives at the receive array. Therefore, each scatterer defines a signal path between the transmit and the receive array and the resulting channel matrix describes a multipath environment. The function works with antenna arrays of arbitrary size at any designated frequency band.
Improve SNR by Array Gain for Line of Sight Propagation
The simplest wireless channel is a line of sight (LOS) propagation. Although simple, such channels can often be found in rural areas. Adopting an antenna array under such situations can improve the signal to noise ratio at the receiver and in turn improve the communication link's bit error rate (BER).
SISO LOS Channel
Before discussing the performance of a MIMO system, it is useful to build a baseline with a single input single output (SISO) communication system. A SISO LOS channel has a direct path from the transmitter to the receiver. Such a channel can be modeled as a special case of the multipath channel.
[~,txang] = rangeangle(rxcenter,txcenter);
[~,rxang] = rangeangle(txcenter,rxcenter);
txsipos = [0;0;0];
rxsopos = [0;0;0];
g = 1; % gain for the path
sisochan = scatteringchanmtx(txsipos,rxsopos,txang,rxang,g);Using BPSK modulation, the bit error rate (BER) for such a SISO channel can be plotted as
Nsamp = 1e6;
x = randi([0 1],Nsamp,1);
ebn0_param = -10:2:10;
Nsnr = numel(ebn0_param);
ber_siso = helperMIMOBER(sisochan,x,ebn0_param)/Nsamp;
helperBERPlot(ebn0_param,ber_siso);
legend('SISO')
SIMO LOS Channel
With the baseline established for a SISO system, this section focuses on the single input multiple output (SIMO) system. In such a system, there is one transmit antenna but multiple receive antennas. Again, it is assumed that there is a direct path between the transmitter and the receiver.
Assume the receive array is a 4-element ULA with half-wavelength spacing, then the SIMO channel can be modeled as
rxarray = phased.ULA('NumElements',4,'ElementSpacing',lambda/2); rxmopos = getElementPosition(rxarray)/lambda; simochan = scatteringchanmtx(txsipos,rxmopos,txang,rxang,g);
In the SIMO system, because the received signals across receive array elements are coherent, it is possible to steer the receive array toward the transmitter to improve the SNR. Note that this assumes that the signal incoming direction is known to the receiver. In reality, the angle is often obtained using direction of arrival estimation algorithms.
rxarraystv = phased.SteeringVector('SensorArray',rxarray,... 'PropagationSpeed',c); wr = conj(rxarraystv(fc,rxang)); ber_simo = helperMIMOBER(simochan,x,ebn0_param,1,wr)/Nsamp; helperBERPlot(ebn0_param,[ber_siso(:) ber_simo(:)]); legend('SISO','SIMO')

The BER curve shows a gain of 6 dB provided by the receive array.
MISO LOS Channel
The multiple input single output (MISO) system works in a similar way. In this case, the transmitter is a 4-element ULA with half-wavelength spacing.
txarray = phased.ULA('NumElements',4,'ElementSpacing',lambda/2); txmipos = getElementPosition(txarray)/lambda; misochan = scatteringchanmtx(txmipos,rxsopos,txang,rxang,g);
A line of sight MISO system achieves best SNR when the transmitter has the knowledge of the receiver and steers the beam toward the receiver. In addition, to do a fair comparison with the SISO system, the total transmitter power should be the same under both situations.
txarraystv = phased.SteeringVector('SensorArray',txarray,... 'PropagationSpeed',c); wt = txarraystv(fc,txang)'; ber_miso = helperMIMOBER(misochan,x,ebn0_param,wt,1)/Nsamp; helperBERPlot(ebn0_param,[ber_siso(:) ber_simo(:) ber_miso(:)]); legend('SISO','SIMO','MISO')
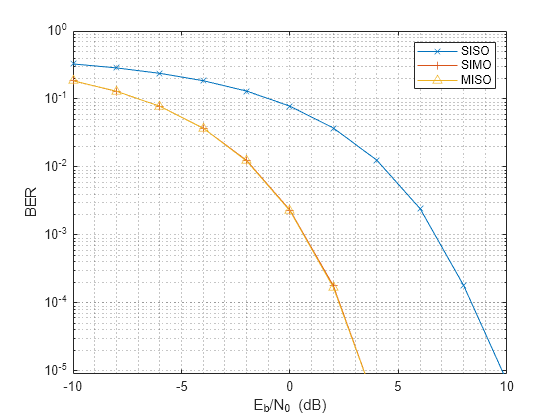
Note that with the pre-steering, the performance of MISO matches the performance of a SIMO system, gaining 6 dB in SNR. It may not be as intuitive compared to the SIMO case because the total transmit power does not increase. However, by replacing a single isotropic antenna with a 4-element transmit array, a 6 dB gain is achieved.
MIMO LOS Channel
Because a SIMO system provides an array gain from the received array and a MISO system provides an array gain from the transmit array, a MIMO system with an LOS propagation can benefit from both the transmit and receive array gain.
Assume a MIMO system with a 4-element transmit array and a 4-element receive array.
mimochan = scatteringchanmtx(txmipos,rxmopos,txang,rxang,g);
To achieve the best SNR, the transmit array and the receive array need to be steered toward each other. With this configuration, the BER curve can be computed as
wt = txarraystv(fc,txang)'; wr = conj(rxarraystv(fc,rxang)); ber_mimo = helperMIMOBER(mimochan,x,ebn0_param,wt,wr)/Nsamp; helperBERPlot(ebn0_param,[ber_siso(:) ber_simo(:) ber_mimo(:)]); legend('SISO','SIMO','MIMO')
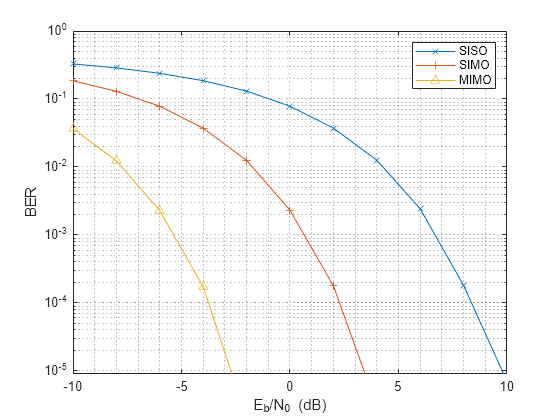
As expected, the BER curve shows that both the transmit array and the receive array contributes a 6 dB array gain, resulting in a total gain of 12 dB over the SISO case.
Improve SNR by Diversity Gain for Multipath Channel
All the channels in the previous sections are line-of-sight channels. Although such channels are found in some wireless communication systems, in general wireless communications occurs in multipath fading environments. The rest of this example explores how using arrays can help in a multipath environment.
SISO Multipath Channel
Assume there are 10 randomly placed scatterers in the channel, then there will be 10 paths from the transmitter to the receiver, as illustrated in the following figure.
Nscat = 10; [~,~,~,scatpos] = ... helperComputeRandomScatterer(txcenter,rxcenter,Nscat); helperPlotSpatialMIMOScene(txsipos,rxsopos,... txcenter,rxcenter,scatpos);

For simplicity, assume that signals traveling along all paths arrive within the same symbol period so the channel is frequency flat.
To simulate the BER curve for a fading channel, the channel needs to change over time. Assume we have 1000 frames and each frame has 10000 bits. The baseline SISO multipath channel BER curve is constructed as
Nframe = 1e3; Nbitperframe = 1e4; Nsamp = Nframe*Nbitperframe; x = randi([0 1],Nbitperframe,1); nerr = zeros(1,Nsnr); for m = 1:Nframe sisompchan = scatteringchanmtx(txsipos,rxsopos,Nscat); wr = sisompchan'/norm(sisompchan); nerr = nerr+helperMIMOBER(sisompchan,x,ebn0_param,1,wr); end ber_sisomp = nerr/Nsamp; helperBERPlot(ebn0_param,[ber_siso(:) ber_sisomp(:)]); legend('SISO LOS','SISO Multipath');

Compared to the BER curve derived from an LOS channel, the BER falls off much slower with the increase of energy per bit to noise power spectral density ratio (Eb/N0) due to the fading caused by the multipath propagation.
SIMO Multipath Channel
As more receive antennas are used in the receive array, more copies of the received signals are available at the receiver. Again, assume a 4-element ULA at the receiver.
The optimal combining weights can be derived by matching the channel response. Such a combining scheme is often termed as maximum ratio combining (MRC). Although in theory such scheme requires the knowledge of the channel, in practice the channel response can often be estimated at the receive array.
nerr = zeros(1,Nsnr); for m = 1:Nframe simompchan = scatteringchanmtx(txsipos,rxmopos,Nscat); wr = simompchan'/norm(simompchan); nerr = nerr+helperMIMOBER(simompchan,x,ebn0_param,1,wr); end ber_simomp = nerr/Nsamp; helperBERPlot(ebn0_param,[ber_sisomp(:) ber_simomp(:)]); legend('SISO Multipath','SIMO Multipath');

Note that the received signal is no longer weighted by a steering vector toward a specific direction. Instead, the receiving array weights in this case are given by the complex conjugate of the channel response. Otherwise it is possible that multipath could make the received signal out of phase with the transmitted signal. This assumes that the channel response is known to the receiver. If the channel response is unknown, pilot signals can be used to estimate the channel response.
It can be seen from the BER curve that not only the SIMO system provides some SNR gains compared to the SISO system, but the slope of the BER curve of the SIMO system is also steeper compared to the BER curve of the SISO system. The gain resulted from the slope change is often referred to as the diversity gain.
MISO Multipath Channel
Things get more interesting when there is multipath propagation in a MISO system. First, if the channel is known to the transmitter, then the strategy to improve the SNR is similar to maximum ratio combining. The signal radiated from each element of the transmit array should be weighted so that the propagated signal can be added coherently at the receiver.
nerr = zeros(1,Nsnr); for m = 1:Nframe misompchan = scatteringchanmtx(txmipos,rxsopos,Nscat); wt = misompchan'/norm(misompchan); nerr = nerr+helperMIMOBER(misompchan,x,ebn0_param,wt,1); end ber_misomp = nerr/Nsamp; helperBERPlot(ebn0_param,[ber_sisomp(:) ber_simomp(:) ber_misomp(:)]); legend('SISO Multipath','SIMO Multipath','MISO Multipath');

Note the transmit diversity gain shown in the BER curve. Compared to the SIMO multipath channel case, the performance of a MISO multipath system is not as good. This is because there is only one copy of the received signal yet the transmit power gets spread among multiple paths. It is certainly possible to amplify the signal at the transmit side to achieve an equivalent gain, but that introduces additional cost.
If the channel is not known to the transmitter, there are still ways to explore the diversity via space time coding. For example, Alamouti code is a well known coding scheme that can be used to achieve diversity gain when the channel is not known. Interested readers are encouraged to explore the Introduction to MIMO Systems example in Communications Toolbox™.
MIMO Multipath Channel
The rest of this example focuses on a multipath MIMO channel. In particular, this section illustrates the case where the number of scatterers in the environment is larger than the number of elements in the transmit and receive arrays. Such an environment is often termed as a rich scattering environment.
Before diving into the specific performance measures, it is helpful to get a quick illustration of what the channel looks like. The following helper function creates a 4x4 MIMO channel where both transmitter and receiver are 4-element ULAs.
[txang,rxang,scatg,scatpos] = ...
helperComputeRandomScatterer(txcenter,rxcenter,Nscat);
mimompchan = scatteringchanmtx(txmipos,rxmopos,txang,rxang,scatg);There are multiple paths available between the transmit array and the receive array because of the existence of the scatterers. Each path consists of a single bounce off the corresponding scatterer.
helperPlotSpatialMIMOScene(txmipos,rxmopos,txcenter,rxcenter,scatpos);

There are two ways to take advantage of a MIMO channel. The first way is to explore the diversity gain offered by a MIMO channel. Assuming the channel is known, the following figure shows the diversity gain with the BER curve.
nerr = zeros(1,Nsnr); for m = 1:Nframe mimompchan = scatteringchanmtx(txmipos,rxmopos,Nscat); [u,s,v] = svd(mimompchan); wt = u(:,1)'; wr = v(:,1); nerr = nerr+helperMIMOBER(mimompchan,x,ebn0_param,wt,wr); end ber_mimomp = nerr/Nsamp; helperBERPlot(ebn0_param,[ber_sisomp(:) ber_simomp(:) ber_mimomp(:)]); legend('SISO Multipath','SIMO Multipath','MIMO Multipath');
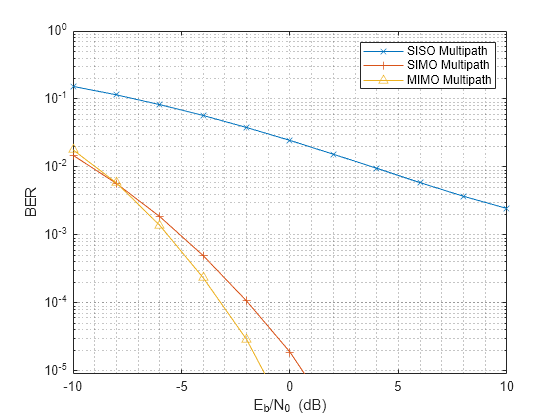
Compare the BER curve from a MIMO channel with the BER curve obtained from a SIMO system. In the multipath case, the diversity gain from a MIMO channel is not necessarily better than the diversity gain provided by a SIMO channel. This is because to obtain the best diversity gain, only the dominant mode in a MIMO channel is used yet there are other modes in the channel that are not used. So is there an alternative way to utilize the channel?
Improve Capacity by Spatial Multiplexing for MIMO Multipath Channel
The answer to the previous question lies in a scheme called spatial multiplexing. The idea behind spatial multiplexing is that a MIMO multipath channel with a rich scatterer environment can send multiple data streams simultaneously across the channel. For example, the channel matrix of a 4x4 MIMO channel becomes full rank because of the scatterers. This means that it is possible to send as many as 4 data streams at once. The goal of spatial multiplexing is less about increasing the SNR but more about increasing the information throughput.
The idea of spatial multiplexing is to separate the channel matrix to multiple mode so that the data stream sent from different elements in the transmit array can be independently recovered from the received signal. To achieve this, the data stream is precoded before the transmission and then combined after the reception. The precoding and combining weights can be computed from the channel matrix by
[wp,wc] = diagbfweights(mimompchan);
To see why the combination of the precoding and combining weights can help transmit multiple data streams at the same time, examine the product of the weights and the channel matrix.
wp*mimompchan*wc
ans = 4×4 complex
10.3543 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i
-0.0000 + 0.0000i 6.0693 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
-0.0000 + 0.0000i -0.0000 + 0.0000i 2.4446 - 0.0000i -0.0000 + 0.0000i
-0.0000 - 0.0000i 0.0000 - 0.0000i -0.0000 - 0.0000i 1.1049 - 0.0000i
Note that the product is a diagonal matrix, which means that the information received by each receive array element is simply a scaled version of the transmit array element. So it behaves like multiple orthogonal subchannels within the original channel. The first subchannel corresponds to the dominant transmit and receive directions so there is no loss in the diversity gain. In addition, it is now possible to use other subchannels to carry information too, as shown in the BER curve for the first two subchannels.
Ntx = 4; Nrx = 4; x = randi([0 1],Nbitperframe,Ntx); nerr = zeros(Nrx,Nsnr); for m = 1:Nframe mimompchan = scatteringchanmtx(txmipos,rxmopos,Nscat); [wp,wc] = diagbfweights(mimompchan); nerr = nerr+helperMIMOMultistreamBER(mimompchan,x,ebn0_param,wp,wc); end ber_mimompdiag = nerr/Nsamp; helperBERPlot(ebn0_param,[ber_sisomp(:) ber_mimomp(:)... ber_mimompdiag(1,:).' ber_mimompdiag(2,:).']); legend('SISO LOS','MIMO Multipath','MIMO Multipath Stream 1',... 'MIMO Multipath Stream 2');
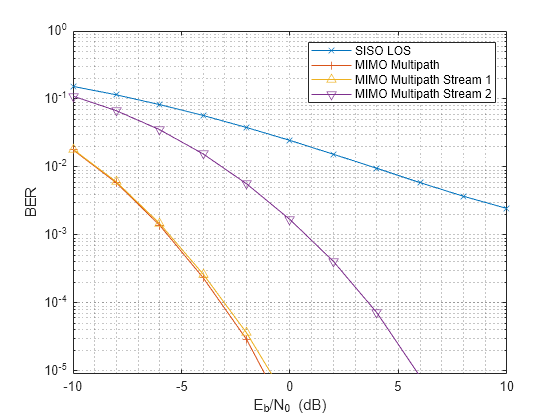
Although the second stream cannot provide a gain as high as the first stream as it uses a less dominant subchannel, the overall information throughput is improved. Therefore, next section measures the performance by the channel capacity instead of the BER curve.
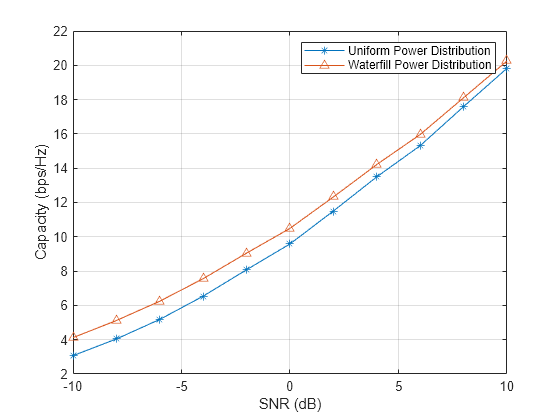
The most intuitive way to transmit data in a MIMO system is to uniformly split the power among transmit elements. However, the capacity of the channel can be further improved if the channel is known at the transmitter. In this case, the transmitter could use the waterfill algorithm to make the choice of transmitting only in the subchannels where a satisfying SNR can be obtained. The following figure shows the comparison of the system capacity between the two power distribution schemes. The result confirms that the waterfill algorithm provides a better system capacity compared to the uniform power distribution. The difference gets smaller when the system level SNR improves.
C_mimo_cu = zeros(1,Nsnr); C_mimo_ck = zeros(1,Nsnr); Ntrial = 1000; for m = 1:Nsnr for n = 1:Ntrial mimompchan = scatteringchanmtx(txmipos,rxmopos,Nscat); N0 = db2pow(-ebn0_param(m)); [~,~,~,~,cu] = diagbfweights(mimompchan,1,N0,'uniform'); [~,~,~,~,ck] = diagbfweights(mimompchan,1,N0,'waterfill'); C_mimo_cu(m) = C_mimo_cu(m)+cu; C_mimo_ck(m) = C_mimo_ck(m)+ck; end end C_mimo_cu = C_mimo_cu/Ntrial; C_mimo_ck = C_mimo_ck/Ntrial; plot(ebn0_param,C_mimo_cu(:),'-*',ebn0_param,C_mimo_ck(:),'-^'); xlabel('SNR (dB)'); ylabel('Capacity (bps/Hz)'); legend('Uniform Power Distribution','Waterfill Power Distribution'); grid on;
For more details on spatial multiplexing and its detection techniques, refer to the Spatial Multiplexing example in Communications Toolbox.
From Beamforming to Precoding
Finally, it is worth looking at how these different ways of using arrays relate to each other. Starting from the LOS channel, as mentioned in the previous sections, the benefit provided by the array is an improvement in the SNR.
[~,txang] = rangeangle(rxcenter,txcenter);
[~,rxang] = rangeangle(txcenter,rxcenter);
mimochan = scatteringchanmtx(txmipos,rxmopos,txang,rxang,1);
wt = txarraystv(fc,txang)';
wr = conj(rxarraystv(fc,rxang));
helperPlotSpatialMIMOScene(txmipos,rxmopos,txcenter,rxcenter,...
(txcenter+rxcenter)/2,wt,wr)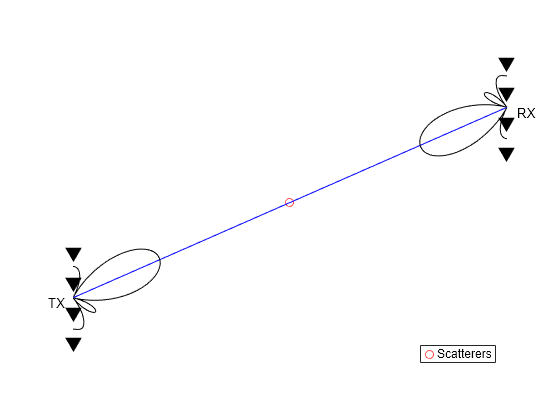
It is clear from the sketch that in this case, the transmit and receive weights form two beams that point to each other. Thus, the array gain is achieved by the beamforming technique. On the other hand, if one tries to create a similar sketch for a MIMO channel, it looks like the following figure.
[txang,rxang,scatg,scatpos] = ... helperComputeRandomScatterer(txcenter,rxcenter,Nscat); mimompchan = scatteringchanmtx(txmipos,rxmopos,txang,rxang,scatg); [wp,wc] = diagbfweights(mimompchan); helperPlotSpatialMIMOScene(txmipos,rxmopos,txcenter,rxcenter,... scatpos,wp(1,:),wc(:,1))
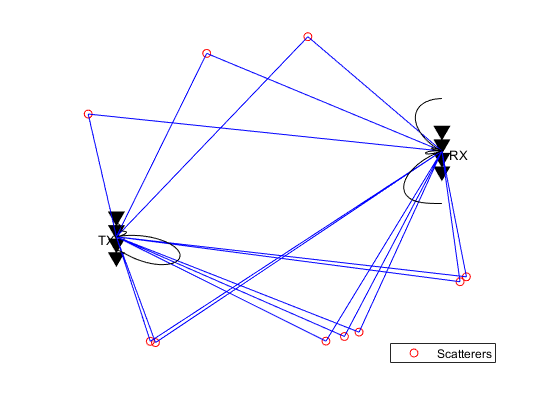
Note that the figure only depicts the pattern for the first data stream but nevertheless it is clear that the pattern no longer necessarily has a dominant main beam. However, if the number of scatterers is reduced to one, then the scene becomes
[txang,rxang,scatg,scatpos] = ... helperComputeRandomScatterer(txcenter,rxcenter,1); mimompchan = scatteringchanmtx(txmipos,rxmopos,txang,rxang,scatg); [wp,wc] = diagbfweights(mimompchan); helperPlotSpatialMIMOScene(txmipos,rxmopos,txcenter,rxcenter,... scatpos,wp(1,:),wc(:,1))
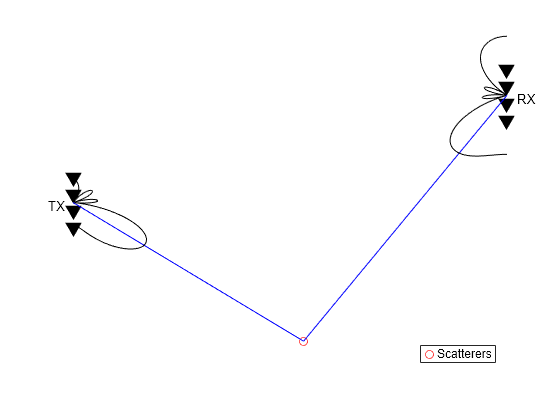
Therefore, the LOS channel case, or more precisely, the one scatterer case, can be considered as a special case of the precoding. When there is only one path available between the transmit and receive arrays, the precoding degenerates to a beamforming scheme.
Improve Capacity by Polarization Multiplexing
As shown in this example so far, the key to simultaneously support multiple users in a communication channel is to divide the channel resources among users. Traditionally, resources are divided in either time or frequency domains. This example has shown that the resources can also be divided spatially. If the subchannels are orthogonal to each other in space, no interference is introduced among users. At the end of this example, it is worth mentioning another dimension of the resource that can be used to support multiple users, which is polarization.
All antennas are polarized. Therefore, it is possible to separate two users if their antennas are orthogonal in polarization. This principle is explored in a popular array configuration in the 3GPP standard [3], where the antenna array is a uniform rectangular array; but at each element position, there are two antennas with orthogonal polarizations. These two collocated antennas can be considered as a special two-element array where the two antennas are not separated in space but separated in polarization.
The code below models such an array. Two orthogonal dipoles are deployed at each location. For the sake of comparison, a 4-element panel array is used. Furthermore, the elements of the same polarization within the panel share a common radio frequency (RF) module so there is one data stream for each polarization.
ant1 = phased.ShortDipoleAntennaElement('AxisDirection','z'); ant2 = phased.ShortDipoleAntennaElement('AxisDirection','y'); polarray = phased.NRRectangularPanelArray('ElementSet',{ant1,ant2},... 'Size',[1 4 1 1],'EnablePanelSubarray',true);
Next, set up a channel. To illustrate the benefit of polarization multiplexing, a line-of-sight (LOS) is used. Therefore, using the antenna array defined above, the system has 2 transmit ports and 2 receive ports. If the polarization multiplexing works as expected, then such a system can simultaneously support 2 data streams, just like 2 SISO channels.
txpos = [0;0;0]; rxpos = [1;0;0]; txax = azelaxes(0,0); rxax = azelaxes(180,0); mimopolchan = phased.ScatteringMIMOChannel('TransmitArray',polarray,... 'ReceiveArray',polarray,'Polarization','combined',... 'TransmitArrayPosition',txpos,'TransmitArrayOrientationAxes',txax,... 'ReceiveArrayPosition',rxpos,'ReceiveArrayOrientationAxes',rxax,... 'SimulateDirectPath',true,'NumScatterers',0);
Next, simulate the BER curve
x = randi([0 1],Nbitperframe,2); nerr = zeros(2,Nsnr); for m = 1:Nframe nerr = nerr+helperPolMIMOBER(mimopolchan,x,ebn0_param); end ber_polmimo = nerr/Nsamp; helperBERPlot(ebn0_param,[ber_siso(:)... ber_polmimo(1,:).' ber_polmimo(2,:).']); legend('SISO LOS','MIMO Polarization 1 LOS','MIMO Polarization 2 LOS');
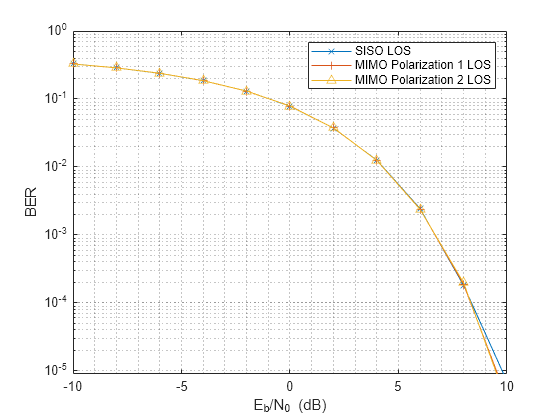
The plot shows that the polarization multiplexing performs just like two SISO channels, as expected. In addition, polarization multiplexing is desirable because it is a multiple access scheme used with other multiple access techniques, such as spatial multiplexing. On the other hand, polarization can be decomposed into two orthogonal components, which means realistically it can at best double the channel capacity.
Summary
This example explains how array processing can be used to improve the quality of a MIMO wireless communication system. Depending on the nature of the channel, the arrays can be used to either improve the SNR via array gain or diversity gain, or improve the capacity via spatial multiplexing and polarization multiplexing. The example also shows how to use functions like scatteringchanmtx and diagbfweights to simulate those scenarios. For more information on MIMO systems modeling, interested readers may refer to examples provided in Communications Toolbox.
Reference
[1] David Tse and Pramod Viswanath, Fundamentals of Wireless Communications, Cambridge, 2005
[2] Arogyswami Paulraj, Introduction to Space-Time Wireless Communication, Cambridge, 2003
[3] 3GPP TR 38.901 verstion 16.1.0 Release 16