Main Content

Power Converter Aging Severity Detection

Open Live Script

Power converters are used to change electrical energy from one form to another to meet the requirements of the applications they support. They are a key part of electrical devices across several industries such as consumer electronics, renewable energy systems, and industrial equipment. Two of the common causes of power converter degradation are capacitor and semiconductor degradation. In this example, a power converter modeled in Simscape™ Electrical™ is used to simulate semiconductor based degradation in IGBT switches. This synthetic data is used to build a predictive maintenance algorithm that can detect aging severity of the power converter.

Load the Model

mdl = 'Three_Phase_Inverter.slx';
load_system(mdl);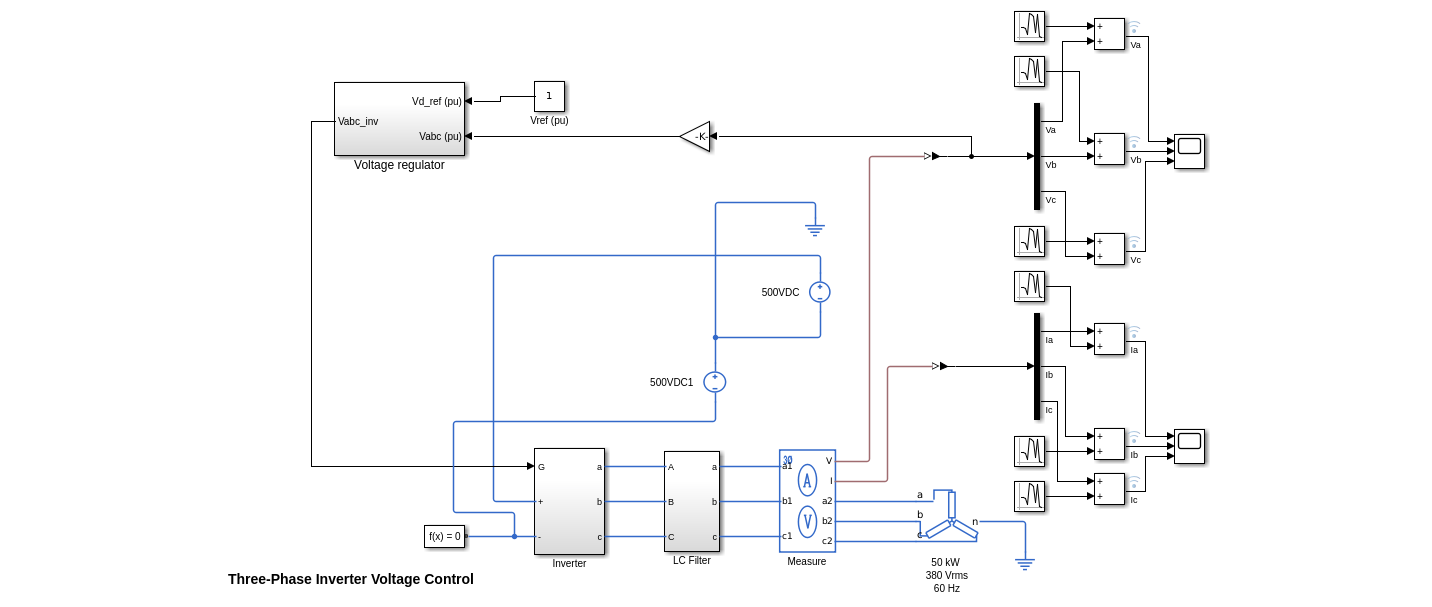

mdl.png

The model represents a three-phase inverter that uses an ideal voltage source. The model includes the following elements:

  • A three-phase inverter consists of six IGBTs (Insulated Gate Bipolar Transistors), two for each phase.

  • An LC filter to smooth out switching noise, and voltage fluctuations.

  • A voltage regulator to provide a stable and consistent output voltage regardless of variations in input voltage or load conditions.

Generate Data for Different Aging Severities

As IGBTs age, degradation leads to changes that impact performance, reliability, and overall lifespan. Age-induced degradation changes include the following primary characteristics:

  • Threshold voltage: Minimum gate-emitter voltage required to turn on the IGBT and allow a significant current to flow between the collector and emitter.

  • Transconductance: Change in the collector current per unit change in the gate-emitter voltage, while keeping the collector-emitter voltage constant.

  • On-state resistance: The resistance encountered by the current flowing through the IGBT when it is in the on-state.

The example focuses on simulating a changing on-state resistance to model aging of the IGBT. When the device is at the end of its life, the on-state resistance decreases by about 20% to 25% compared to its nominal value [1]. Note that on-state resistance cannot be directly measured. Instead the output voltage and current are used to estimate the on-state resistance.

Vary the on-state resistance by changing the RON parameter of the IGBT blocks in the model to simulate aging of the power converter. For each simulation, one of the six IGBTs are selected at random and its RON value is set to a value indicating either healthy or degraded states. Simulink.SimulationInput objects are created with selected resistance value for the IGBT of choice. Random noise is added to current and voltage measurement to mimic real world conditions. To train a machine learning model to distinguish between the different aging states, generate twenty simulations for each aging state. Define the RON values as defined in [1]. Define the location of aging and aging severity of the selected switch for each simulation. 

RON = [7e-3,6.3e-3,5.7e-3,5e-3]; 
AgingSeverity = ["Healthy", "Mild", "Moderate", "High"];
blockPath = "Three_Phase_Inverter/Inverter/";
locn = ["AH", "AL", "BH", "BL", "CH", "CL"];
scn = {'.. Generating Healthy data!';'.. Generating aging data for phase A';...
      '.. Generating aging data for phase B';'.. Generating aging data for phase C'; };

numSimPerSeverity = 20;
agingLocation = repmat([1,2;3,4;5,6],[1, ceil(numSimPerSeverity/2)]);
ageSeverity = repmat([2 2 3 3 4 4],[1, ceil(numSimPerSeverity/6)]);

Create Simulink.SimulationInput objects for each aging parameter choice:

simin = Simulink.SimulationInput.empty;
for iScn = 1:length(scn)
    for iSim = 1:numSimPerSeverity
        simin(end+1) = Simulink.SimulationInput(mdl);
        if iScn == 1            
            selectedLocation = randsample(1:6,1);

            blockPath_ = strjoin([blockPath,locn(selectedLocation)], '');
            Ron = RON(iScn);            

            fileName = ['Test_data_Healthy_file_',num2str(iSim),'.xlsx'];
            simin(end) = simin(end).setBlockParameter(blockPath_, 'Ron', num2str(Ron));
        else
            selectedLocation = agingLocation(iScn-1,iSim);
            selectedSeverity = ageSeverity(iSim);

            blockPath_ = strjoin([blockPath,locn(selectedLocation)], '');
            Ron = RON(selectedSeverity);
            simin(end) = simin(end).setBlockParameter(blockPath_, 'Ron', num2str(Ron));        
        end
    end
end

Use the generateSimulationEnsemble function to run the simulations defined by the Simulink.SimulationInput objects defined above and store the results in a folder called Data.

if ~isfolder("Data")
    mkdir("Data");
end

generateSimulationEnsemble(simin, 'Data', 'ShowProgress',false);

Create a simulationEnsembleDatastore from the stored results in the Data folder. Generate the value for the condition variable called AgingSeverity for each mat file in the Data folder using the RON parameter value.

sens = simulationEnsembleDatastore('Data');

sens.SelectedVariables = "SimulationInput";
sens.ConditionVariables = "AgingSeverity";

reset(sens);

while hasdata(sens)
    data = read(sens);
    Ron = str2double(data.SimulationInput{1}.BlockParameters.Value);    
    [~, loc] = min(abs(Ron-RON));   
    writeToLastMemberRead(sens,'AgingSeverity',AgingSeverity(loc));
end

Read the Generated Data into MATLAB for Feature Extraction

Read all the data into MATLAB workspace for feature extraction and model training. Plot the current meausrement Ia from one of the Healthy and High aging severity datasets to visualize any differences between the two cases. 

sens.SelectedVariables = ["Ia", "Ib", "Ic", "Va", "Vb", "Vc", "AgingSeverity"];

measuredData = readall(sens);

tiledlayout;
nexttile;
Ia_healthy = measuredData.Ia{find(measuredData.AgingSeverity == "Healthy", 1)}; 
plot(Ia_healthy.Time, Ia_healthy.Data, '--'); hold on;
Ia_high_severity = measuredData.Ia{find(measuredData.AgingSeverity == "High", 1)};
plot(Ia_high_severity.Time, Ia_high_severity.Data, '-.'); hold off;
legend(["Healthy", "High Severity"]);
title("Current Measurement on First Phase");
nexttile;
Vb_healthy = measuredData.Vb{find(measuredData.AgingSeverity == "Healthy", 1)};
plot(Vb_healthy.Time, Vb_healthy.Data, '--'); hold on;
Vb_high_severity = measuredData.Vb{find(measuredData.AgingSeverity == "High", 1)};
plot(Vb_high_severity.Time, Vb_high_severity.Data, '-.'); hold off;
legend(["Healthy", "High Severity"]);
title("Voltage Measurement on Second Phase");

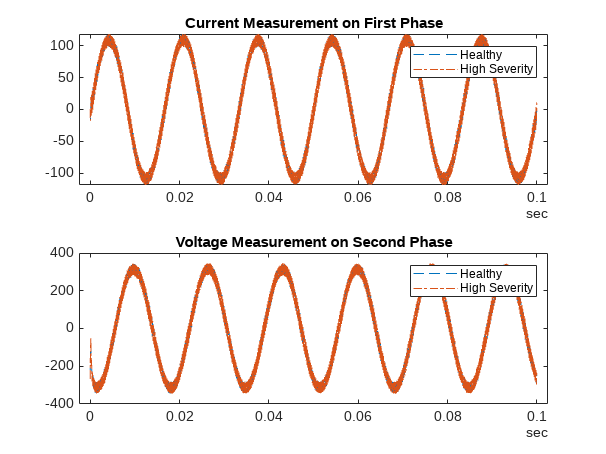
Figure contains 2 axes objects. Axes object 1 with title Current Measurement on First Phase contains 2 objects of type line. These objects represent Healthy, High Severity. Axes object 2 with title Voltage Measurement on Second Phase contains 2 objects of type line. These objects represent Healthy, High Severity.

As seen in the plots, the current measurements for the two cases looks similar making very difficult to distinguish between them visually. To identify characteristics that can be used to distinguish between the various aging severity conditions, extract time-domain and frequency-domain features from the data.

Open the Diagnostic Feature Designer app with measuredData specified as the input argument. As an alternative to using the app itself, you can use app-generated MATLAB code from a previous session. Set openDFDApp to false to use the code in diagnosticFeatures_IGBT and to true to open the app. 

openDFDApp = false;
if openDFDApp
    diagnosticFeatureDesigner(measuredData);
else
    FeatureTable = diagnosticFeatures_IGBT(measuredData);
end
Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 8 workers.

In the DFD App, import the data and select all the imported signals for Time Domain Signal Features computation:

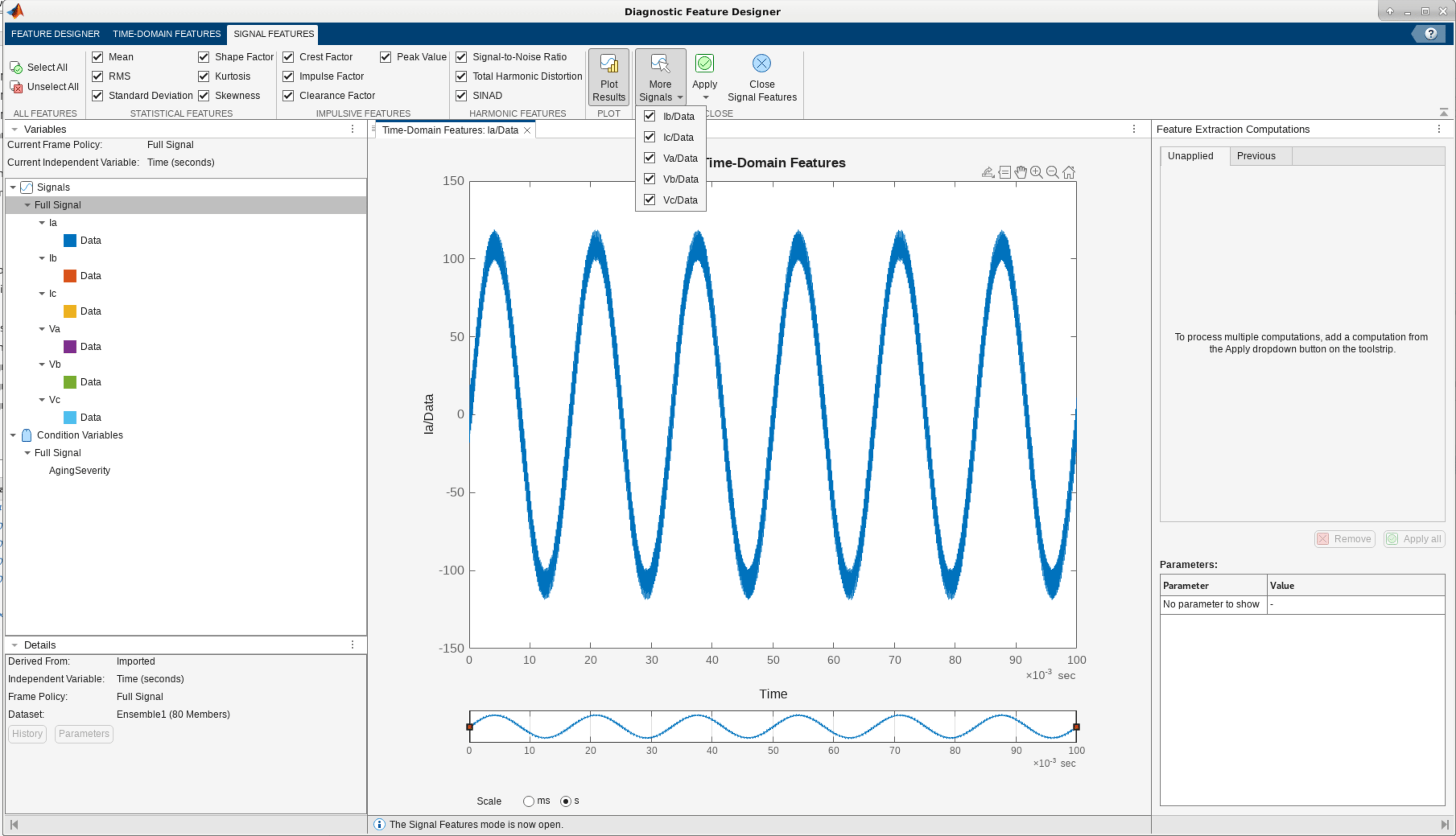
Screenshot 2024-06-25 at 10.29.51�AM.png

The current and voltage measurements for each of the phases are sinusoidal signals. For such signals, frequency domain features capture key characteristics such as peak amplitudes and location which tend to vary as the system behavior evolves. In the app, compute the power spectrum using Welch's method for all the imported signals and then spectral features in the Frequency Domain features menu:

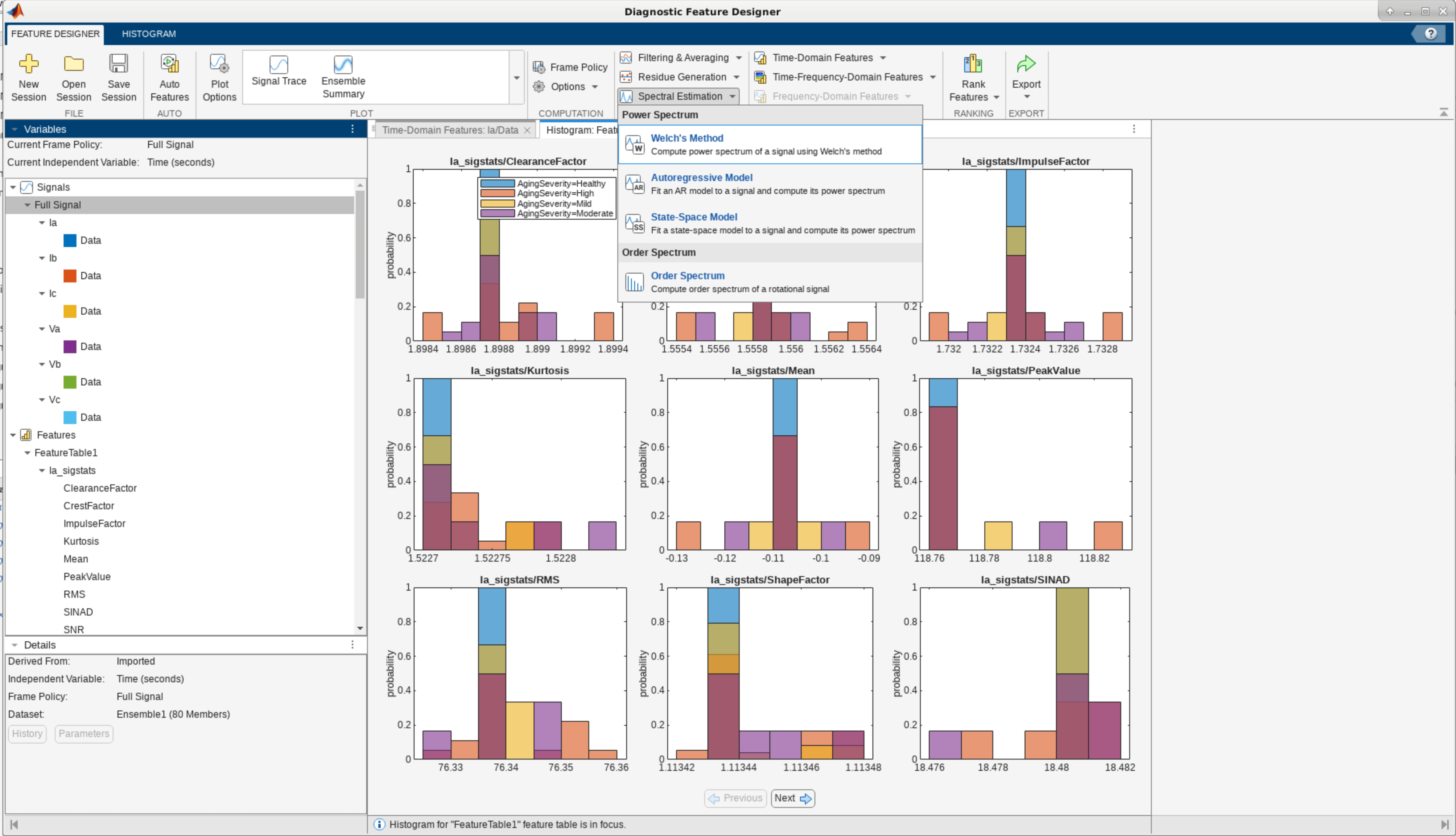
Screenshot 2024-06-25 at 11.15.14�AM.png

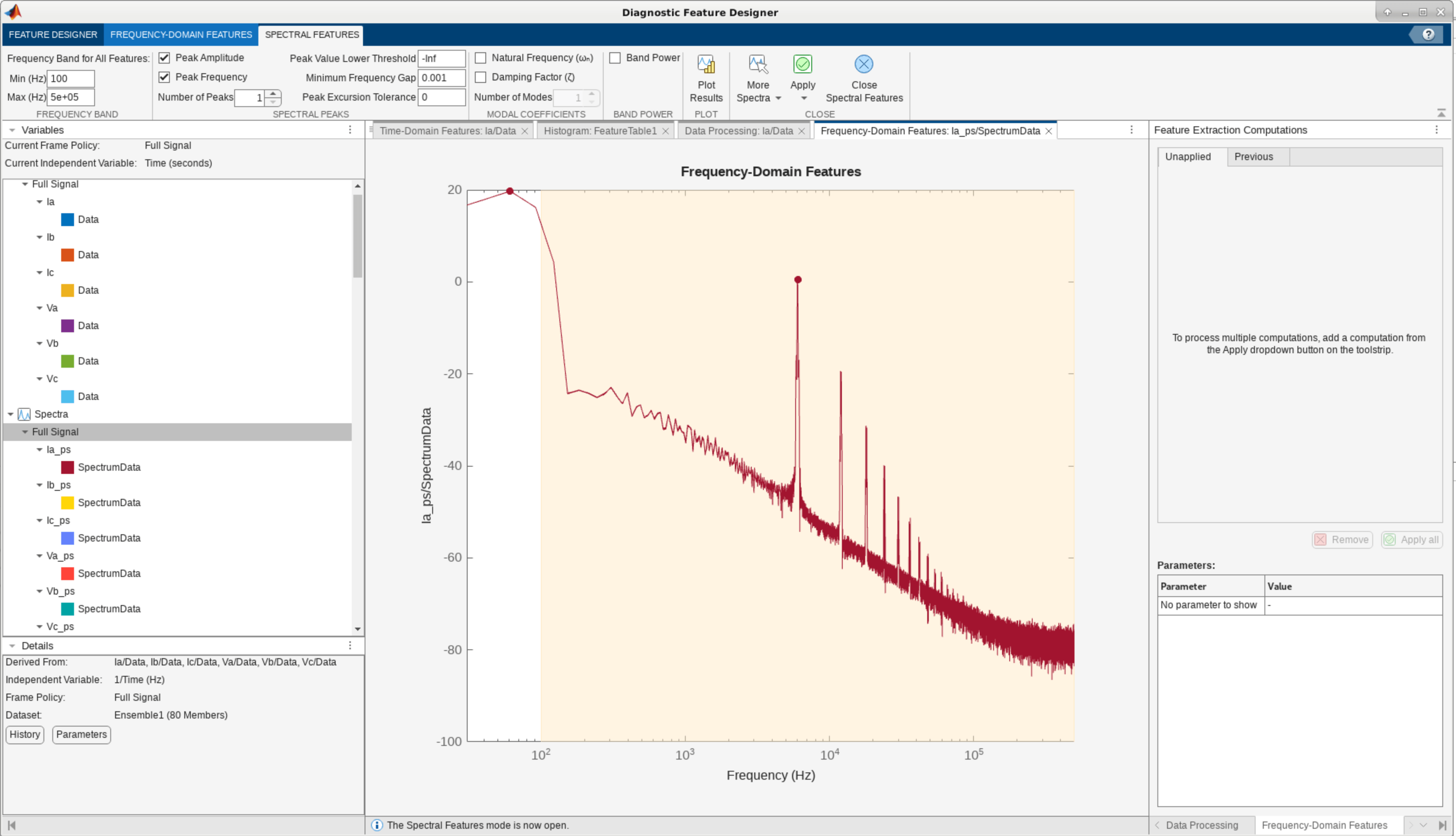
Screenshot 2024-06-25 at 11.30.41�AM.png

Rank the features using the default One-way Anova method and export the top fifteen features to the MATLAB workspace. Also export a MATLAB function to use later in the example for deployment. Use Generate Features for Features and select Format for streaming data. Press the OK button and name the saved function as diagnosticFeatures_streaming_IGBT.m:

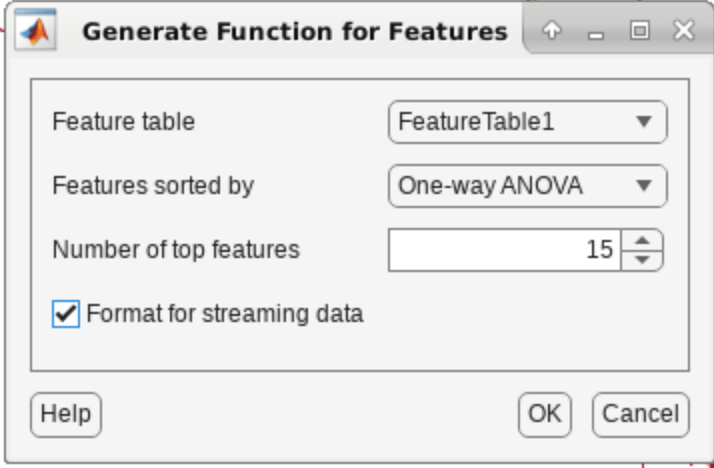
Screenshot 2024-06-25 at 11.31.26�AM.png

head(FeatureTable,5);
    AgingSeverity    Ia_sigstats/THD    Ic_sigstats/ClearanceFactor    Ic_sigstats/CrestFactor    Ic_sigstats/ImpulseFactor    Ic_sigstats/PeakValue    Ic_sigstats/THD    Va_sigstats/Kurtosis    Va_sigstats/THD    Vc_sigstats/THD    Ia_ps_spec/PeakAmp1    Ib_ps_spec/PeakAmp1    Ic_ps_spec/PeakAmp1    Va_ps_spec/PeakAmp1    Vb_ps_spec/PeakAmp1    Vc_ps_spec/PeakAmp1
    _____________    _______________    ___________________________    _______________________    _________________________    _____________________    _______________    ____________________    _______________    _______________    ___________________    ___________________    ___________________    ___________________    ___________________    ___________________

      "Healthy"          -28.468                  1.9023                       1.5578                      1.7353                      118.7                -28.677               1.5228               -28.461            -28.683              1.1063                 1.1053                 1.1137                 9.2235                 9.2155                  9.285       
      "Healthy"          -28.468                  1.9023                       1.5578                      1.7353                      118.7                -28.677               1.5228               -28.461            -28.683              1.1063                 1.1053                 1.1137                 9.2235                 9.2155                  9.285       
      "Healthy"          -28.468                  1.9023                       1.5578                      1.7353                      118.7                -28.677               1.5228               -28.461            -28.683              1.1063                 1.1053                 1.1137                 9.2235                 9.2155                  9.285       
      "Healthy"          -28.468                  1.9023                       1.5578                      1.7353                      118.7                -28.677               1.5228               -28.461            -28.683              1.1063                 1.1053                 1.1137                 9.2235                 9.2155                  9.285       
      "Healthy"          -28.468                  1.9023                       1.5578                      1.7353                      118.7                -28.677               1.5228               -28.461            -28.683              1.1063                 1.1053                 1.1137                 9.2235                 9.2155                  9.285       

gplotmatrix(FeatureTable{:, 2:6}, [], FeatureTable.AgingSeverity)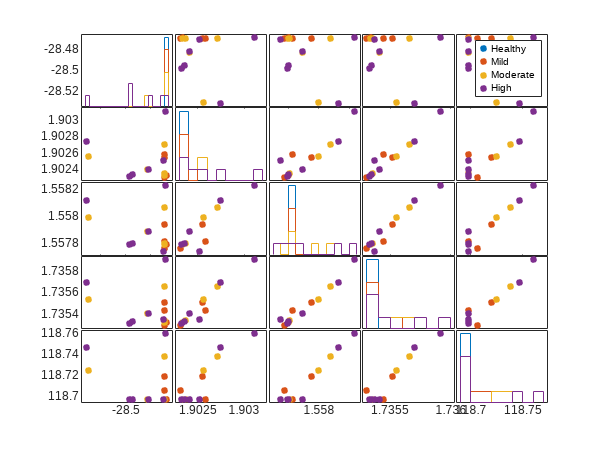

Figure contains 30 axes objects. Axes object 1 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 2 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 3 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 4 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 5 contains 4 objects of type line. Axes object 6 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 7 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 8 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 9 contains 4 objects of type line. Axes object 10 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 11 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 12 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 13 contains 4 objects of type line. Axes object 14 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 15 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 16 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 17 contains 4 objects of type line. Axes object 18 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 19 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 20 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 21 contains 4 objects of type line. Axes object 22 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 23 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 24 contains 4 objects of type line. One or more of the lines displays its values using only markers Axes object 25 contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Healthy, Mild, Moderate, High. Hidden axes object 26 contains 4 objects of type histogram. Hidden axes object 27 contains 4 objects of type histogram. Hidden axes object 28 contains 4 objects of type histogram. Hidden axes object 29 contains 4 objects of type histogram. Hidden axes object 30 contains 4 objects of type histogram.

Train a Model to Detect the Aging Severity

Use the cvpartition function to partition the data in FeatureTable into training and test partitions to use for training and validating a machine learning model. Set the random number generator to default to ensure repeatability of results in the example.

rng("default")

n = height(FeatureTable);
hpartition = cvpartition(n,'Holdout',0.3);
idxTrain = training(hpartition);
FeatureTable_Train = FeatureTable(idxTrain,:);
idxTest = test(hpartition);
FeatureTable_Test = FeatureTable(idxTest,:);

To find a suitable machine learning model, use fitcauto function to automatically select a classification model with optimized hyperparameters. Given predictor and response data, fitcauto automatically tries a selection of classification model types with different hyperparameter values. Limit the model space to "svm" to obtain faster search and training time for this example. Also set the MaxObjectiveEvaluations to 30 increase the number of hyperparameter options that the function searches. Set MaxTime to 60 to limit the time spent searching for the best model and hyperparameters. These values are picked based on experimentation and might need to be changed to suit other datasets.

mdl = fitcauto(FeatureTable_Train, "AgingSeverity", "Learners", ["svm"],...
    "HyperparameterOptimizationOptions", struct("UseParallel",true, "Verbose", 0, "showplot", false, "MaxObjectiveEvaluations", 40, "MaxTime", 60));

Validate the trained model with test data and generate a confusion matrix to visualize the performance of the trained model for the test dataset. 

[eSeverity, eScores] = mdl.predict(FeatureTable_Test);

confusionchart(FeatureTable_Test.AgingSeverity, string(eSeverity))

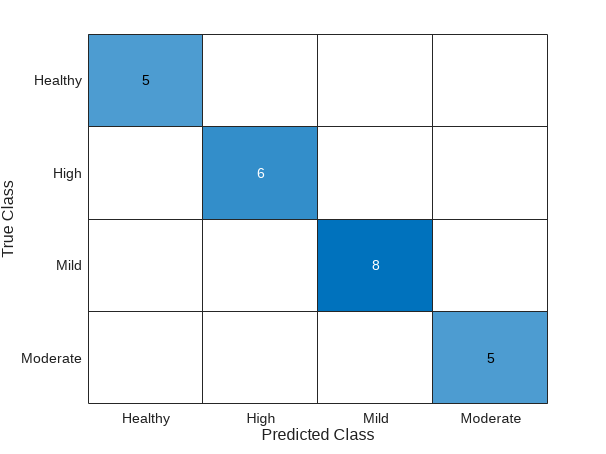
Figure contains an object of type ConfusionMatrixChart.

The confusion chart indicates that the selected model is able to identify the different aging severities accurately.

Generate a mex file for Selected Model and Validate Performance

Now that you have identified a suitable model with good performance, generate code for this algorithm. This process includes generating code for feature extraction and model inference. To generate MATLAB code suitable for C/C++ code generation in the app, use the diagnosticFeatures_streaming_IGBT.m file that you generated previously.

To prepare for code generation, save the trained model using saveLearnerForCoder function: 

testData = measuredData(1,:);
saveLearnerForCoder(mdl,'SVMModel');

Create a function called classifyAgeSeverity.m that accepts testData as input and returns the identified aging severity. 

type("classifyAgeSeverity.m")
function label = classifyAgeSeverity(x) %#codegen
%ClassifyAgeSeverity function accepts a timetable representing the current
%batch of measurements from the power converter system. The predefined
%features are computed. and the trained model is used to detect the
%aging severity of the power converter for this batch of data.

    Mdl = loadLearnerForCoder('SVMModel');
    features = diagnosticFeatures_streaming_IGBT(x);
    label = predict(Mdl,features);
end

Use the codegen function to generate a mex file for the classifyAgeSeverity.m file. 

codegen classifyAgeSeverity -args {testData}
Code generation successful.

Validate the generated mex file by generating a confusion matrix for testdata in MATLAB and from the mex file.

total_test_Samples = 5;
random_Index = randsample(height(measuredData), total_test_Samples);
for rI = 1:total_test_Samples
    testData = measuredData(random_Index(rI), :);
    mlResponse{rI} = classifyAgeSeverity(testData); %#ok<*SAGROW>
    mexResponse{rI} = classifyAgeSeverity(testData);
end

disp('MATLAB Response\n'); 
MATLAB Response\n

disp([mlResponse{:}]);
    {'High'}    {'Mild'}    {'High'}    {'Healthy'}    {'High'}

disp('\nMex Response\n');
\nMex Response\n

disp([mexResponse{:}]);
    {'High'}    {'Mild'}    {'High'}    {'Healthy'}    {'High'}

The results of calling the MATLAB file and mex file for the same input data are identical. The codegen function can be used for other build types such as lib, dll, or exe to suite your application needs.

References

[1] https://eprints.whiterose.ac.uk/135441/1/IECON_2018_Evan_Dimech_John_Dawson_Postprint.pdf