Create Policies and Value Functions
A reinforcement learning policy is a mapping from an environment observation to a probability distribution of the actions to be taken (starting from the state corresponding to the observation). A value (or Q-value) function is a mapping from an environment observation (or observation-action pair) to the value of a policy. The value of a policy is defined as its expected discounted cumulative long-term reward.
Reinforcement learning agents use parametrized policies and value functions, which are implemented by function approximators called actors and critics, respectively. During training, the actor learns the policy that selects the best action to take. It does so by tuning its parameters to assign larger probability to actions that yield the greater values. The critic learns the value (or Q-value) function that estimates the value of the current policy. It does so by tuning its parameters so that the predicted rewards approximate the observed ones.
Before creating a non-default agent, you must create the actor and critic using approximation models such as deep neural networks, linear basis functions, or lookup tables. The type of function approximator and model you can use depends on the type of agent that you want to create.
You can also create policy objects from agents, actors, or critics. You can train these objects using custom loops and deploy them in applications.
The following section are an introduction to actor, critic, and policy objects, as well as their internal approximation models. For an introduction to agents, see Reinforcement Learning Agents.
Actors and Critics
Reinforcement Learning Toolbox™ software supports the following types of actors and critics:
V(S|θV) — Critics that estimate the expected cumulative long-term reward of a policy based on a given observation S. You can create these critics using
rlValueFunction.Q(S,A|θQ) — Critics that estimate the expected cumulative long-term reward of a policy for a given discrete action A and a given observation S. You can create these critics using
rlQValueFunction.Qi(S,Ai|θQ) — Multi-output critics that estimate the expected cumulative long-term reward of a policy for all possible discrete actions Ai given the observation S. You can create these critics using
rlVectorQValueFunction.π(S|θπ) — Actors with a continuous action space that select an action deterministically based on a given observation S, thereby implementing a deterministic policy. You can create these actors using
rlContinuousDeterministicActor.π(S|θπ) — Actors that select an action stochastically (the action is sampled from a probability distribution) based on a given observation S, thereby implementing a stochastic policy. You can create these actors using either
rlDiscreteCategoricalActor(for discrete action spaces) orrlContinuousGaussianActor(for continuous action spaces).
Each approximator uses a set of parameters (θV, θQ, θπ), which are computed during the learning process.
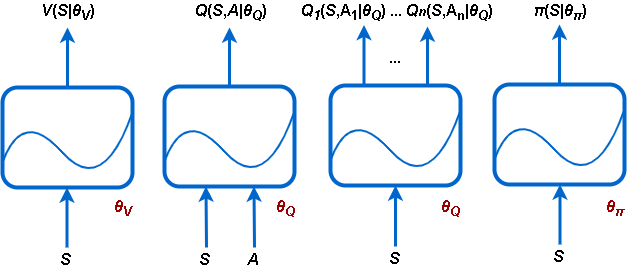
For systems with a limited number of discrete observations and discrete actions, you can store value functions in a lookup table. For systems that have many discrete observations and actions and for observation and action spaces that are continuous, storing the observations and actions is impractical. For such systems, you can represent your actors and critics using deep neural networks or custom (linear in the parameters) basis functions.
The following table summarizes the way in which you can use the six approximator objects available with Reinforcement Learning Toolbox software, depending on the action and observation spaces of your environment, and on the approximation model and agent that you want to use.
How Function Approximators (Actors or Critics) are Used in Agents
| Approximator (Actor or Critic) | Supported Model | Observation Space | Action Space | Supported Agents |
|---|---|---|---|---|
Value function critic V(S), which you create using | Table | Discrete | Not applicable | PG, AC, PPO |
| Deep neural network or custom basis function | Discrete or continuous | Not applicable | PG, AC, PPO | |
| Deep neural network | Discrete or continuous | Not applicable | TRPO | |
Q-value function critic, Q(S,A), which you create using | Table | Discrete | Discrete | Q, DQN, SARSA |
| Deep neural network or custom basis function | Discrete or continuous | Discrete | Q, DQN, SARSA | |
| Continuous | DDPG, TD3, SAC | |||
Multi-output Q-value function critic with a discrete action space Q(S,A), which you create using | Deep neural network or custom basis function | Discrete or continuous | Discrete | Q, DQN, SARSA |
Deterministic policy actor with a continuous action space π(S), which you create using | Deep neural network or custom basis function | Discrete or continuous | Continuous | DDPG, TD3 |
Stochastic policy actor with a discrete action space π(S), which you create using | Deep neural network or custom basis function | Discrete or continuous | Discrete | PG, AC, PPO |
| Deep neural network | Discrete or continuous | Discrete | TRPO | |
Stochastic policy actor with a continuous action space π(S), which you create using | Deep neural network | Discrete or continuous | Continuous | PG, AC, PPO, SAC, TRPO |
Note
rlDiscreteCategoricalActor, which is used in agents such as PG, AC, PPO and
TRPO when the action space is discrete, does not support tables as approximation
model.
You can configure the actor and critic optimization options using the rlOptimizerOptions
object within an agent option object.
Specifically, you can create an agent options object and set its
CriticOptimizerOptions and ActorOptimizerOptions
properties to appropriate rlOptimizerOptions objects. Then you pass the
agent options object to the function that creates the agent.
Alternatively, you can create the agent and then use dot notation to access the
optimization options for the agent actor and critic, for example:
agent.AgentOptions.ActorOptimizerOptions.LearnRate = 0.1;.
For an example on how to create an approximator with a mixed (discrete and continuous)
observation space, see the last examples in rlValueFunction and
rlQValueFunction.
For more information on agents, see Reinforcement Learning Agents.
Policy Objects
You can extract a policy object from an agent using getGreedyPolicy or
getExplorationPolicy, or you can create a policy object from an actor or
critic.
Once you have the policy object, you can then use getAction to
generate deterministic or stochastic actions from it, given an input observation.
Differently from function approximator objects like actors and critics, policy objects do
not have functions that you can use to easily calculate gradients with respect to
parameters. Therefore, policy objects are more tailored toward application deployment,
rather than training. The following table describes the available policy objects.
Policy Objects
Policy Object and getAction Behavior | Distribution and Exploration | Action Space | Approximator Objects Used for Creation | Agents Needed for Extraction |
|---|---|---|---|---|
Generates actions that maximize a discrete action-space Q-value function | Deterministic (no exploration) and greedy. | Discrete | rlQValueFunction or rlVectorQValueFunction
| Q, DQN, SARSA |
Generates either actions that
maximize a discrete action-space Q-value function with probability
| Default: Stochastic (random actions help exploration) | Discrete | rlQValueFunction or rlVectorQValueFunction
| Q, DQN, SARSA |
Generates continuous deterministic actions | Deterministic (no exploration) and greedy. | Continuous | rlContinuousDeterministicActor | DDPG, TD3 |
Generates continuous deterministic actions with added noise according to an internal noise model | Default: Stochastic (noise helps exploration) | Continuous | rlContinuousDeterministicActor | DDPG, TD3 |
Generates stochastic actions according to a probability distribution | Default: Stochastic (random actions help exploration) | Discrete | rlDiscreteCategoricalActor | PG, AC, PPO, TRPO |
| Continuous | rlContinuousGaussianActor | PG, AC, PPO, TRPO, SAC |
Each one of the stochastic policy objects has an option to enable deterministic
behavior, thereby disabling exploration. Except for rlEpsilonGreedyPolicy
and rlAdditiveNoisePolicy, you can use generatePolicyBlock
and generatePolicyFunction to generate a Simulink® block or a function that evaluates the policy, returning an action, for a
given observation input. You can then use the generated function or block to generate code
for application deployment. For more information, see Deploy Trained Reinforcement Learning Policies.
Table Models
Value function approximators (critics) based on lookup tables models are appropriate for environments with a limited number of discrete observations and actions. You can create two types of lookup tables:
Value tables, which store rewards for corresponding observations
Q-tables, which store rewards for corresponding observation-action pairs
To create a table based critic, first create a value table or Q-table using the rlTable function.
Then use the table object as input argument for either rlValueFunction or
rlQValueFunction to
create the approximator object.
Custom Basis Function Models
Custom (linear in the parameters) basis function approximation models have the form
f = W'B, where W is a weight array and
B is the column vector output of a custom basis function that you must
create. The learnable parameters of a linear basis function are the elements of
W.
For value function critics, (such as the ones used in AC, PG or PPO agents),
f is a scalar value, so W must be a column vector
with the same length as B, and B must be a
function of the observation. For more information and examples, see rlValueFunction.
For single-output Q-value function critics, (such as the ones used in Q, DQN, SARSA,
DDPG, TD3, and SAC agents), f is a scalar value, so W
must be a column vector with the same length as B, and
B must be a function of both the observation and action. For more
information and examples, see rlQValueFunction.
For multi-output Q-value function critics with discrete action spaces, (such as those
used in Q, DQN, and SARSA agents), f is a vector with as many elements as
the number of possible actions. Therefore W must be a matrix with as many
columns as the number of possible actions and as many rows as the length of
B. B must be only a function of the observation.
For more information and examples, see rlVectorQValueFunction.
For deterministic actors with a continuous action space (such as the ones in DDPG, and TD3 agents), the dimensions of
fmust match the dimensions of the agent action specification, which is either a scalar or a column vector. For more information and examples, seerlContinuousDeterministicActor.For stochastic actors with a discrete action space (such as the ones in PG, AC, and PPO agents),
fmust be column vector with length equal to the number of possible discrete actions. The output of the actor issoftmax(f), which represents the probability of selecting each possible action. For more information and examples, seerlDiscreteCategoricalActor.For stochastic actors with continuous action spaces cannot rely on custom basis functions (they can only use neural network approximators, due to the need to enforce positivity for the standard deviations). For more information and examples, see
rlContinuousGaussianActor.
For any actor, W must have as many columns as the number of elements
in f, and as many rows as the number of elements in
B. B must be only a function of the observation.
For an example that trains a custom agent that uses a linear basis function, see Create and Train Custom LQR Agent.
Neural Network Models
You can create actor and critic function approximators using deep neural networks models. Doing so uses Deep Learning Toolbox™ software features.
Network Input and Output Dimensions
The dimensions of the network input and output layers for your actor and critic must
match the dimension of the corresponding environment observation and action channels,
respectively. To obtain the action and observation specifications from the environment
env, use the getActionInfo and
getObservationInfo functions, respectively.
actInfo = getActionInfo(env); obsInfo = getObservationInfo(env);
Access the Dimensions property of each channel. For example, get
the size of the first environment and action channel:
actSize = actInfo(1).Dimensions; obsSize = obsInfo(1).Dimensions;
In general actSize and obsSize are row vectors
whose elements are the lengths of the corresponding dimensions. For example, if the first
observation channel is a 256-by-256 RGB image, actSize is the vector
[256 256 3]. To calculate the total number of dimension of the
channel, use prod.For example, assuming the environment has only one
observation channel:
obsDimensions = prod(obsInfo.Dimensions);
For rlVectorQValueFunction critics and rlDiscreteCategoricalActor actors, you need to obtain the number of possible
elements of the action set. You can do so by accessing the Elements
property of the action channel. For example, assuming the environment has only one action
channel:
actNumElements = numel(actInfo.Elements);
Networks for value function critics (such as the ones used in AC, PG, PPO or TRPO
agents) must take only observations as inputs and must have a single scalar output. For
these networks, the dimensions of the input layers must match the dimensions of the
environment observation channels. For more information, see rlValueFunction.
Networks for single-output Q-value function critics (such as the ones used in Q, DQN,
SARSA, DDPG, TD3, and SAC agents) must take both observations and actions as inputs, and
must have a single scalar output. For these networks, the dimensions of the input layers
must match the dimensions of the environment channels for both observations and actions.
For more information, see rlQValueFunction.
Networks for multi-output Q-value function critics (such as those used in Q, DQN, and
SARSA agents) take only observations as inputs and must have a single output layer with
output size equal to the number of possible discrete actions. For these networks the
dimensions of the input layers must match the dimensions of the environment observations
channels. For more information, see rlVectorQValueFunction.
For actor networks, the dimensions of the input layers must match the dimensions of the environment observation channels and the dimension of the output layer must be as follows.
Networks used in actors with a discrete action space (such as the ones in PG, AC, and PPO agents) must have a single output layer with an output size equal to the number of possible discrete actions. For more information, see
rlDiscreteCategoricalActor.Networks used in deterministic actors with a continuous action space (such as the ones in DDPG and TD3 agents) must have a single output layer with an output size matching the dimension of the action space defined in the environment action specification. For more information, see
rlContinuousDeterministicActor.Networks used in stochastic actors with a continuous action space (such as the ones in PG, AC, PPO, and SAC agents) must have a two output layers each with as many elements as the dimension of the action space, as defined in the environment specification. One output layer must produce the mean values (which must be scaled to the output range of the action), and the other must produce the standard deviations of the actions (which must be non-negative). For more information, see
rlContinuousGaussianActor.
Deep Neural Networks
Deep neural networks consist of a series of interconnected layers. You can specify a deep neural network as one of the following:
Array of
LayerobjectsdlnetworkobjectSeriesNetworkobjectlayerGraphobjectDAGNetworkobject
Note
Among the different network objects, dlnetwork is preferred, since it has
built-in validation checks and supports automatic differentiation. If you pass another
network object as an input argument, it is internally converted to a
dlnetwork object. However, best practice is to convert other network
objects to dlnetwork explicitly before using it to
create a critic or an actor for a reinforcement learning agent. You can do so using
dlnet=dlnetwork(net), where net is any neural
network object from the Deep Learning Toolbox. The resulting dlnet is the dlnetwork
object that you use for your critic or actor. This practice allows a greater level of
insight and control for cases in which the conversion is not straightforward and might
require additional specifications.
Typically, you build your neural network by stacking together a number of layers in an
array of Layer objects, possibly adding these arrays to a layerGraph
object, and then converting the final result to a dlnetwork object.
For agents that need multiple input or output layers, you create an array of
Layer objects for each input path (observations or actions) and for
each output path (estimated rewards or actions). You then add these arrays to a layerGraph object
and connect them paths together using the connectLayers
function.
You can also create your deep neural network using the Deep Network Designer app. For an example, see Create DQN Agent Using Deep Network Designer and Train Using Image Observations.
The following table lists some common deep learning layers used in reinforcement learning applications. For a full list of available layers, see List of Deep Learning Layers.
| Deep Learning Toolbox Layer | Description |
|---|---|
featureInputLayer | Inputs feature data. Normalization is not supported. |
imageInputLayer | Inputs vectors and 2-D images. Normalization is not supported. |
sequenceInputLayer | Provides inputs sequence data to a network. Normalization is not supported. |
fullyConnectedLayer | Multiplies the input vector by a weight matrix, and add a bias vector. |
convolution2dLayer | Applies sliding convolutional filters to the input. |
concatenationLayer | Concatenates inputs along a specified dimension. |
additionLayer | Adds the outputs of multiple layers together. |
reluLayer | Sets any input values that are less than zero to zero. |
sigmoidLayer | Applies a sigmoid function to the input such that the output is bounded in the interval (0,1). |
tanhLayer | Applies a hyperbolic tangent activation layer to the input. |
softmaxLayer | Applies a softmax function layer to the input, normalizing it to a probability distribution. |
lstmLayer | Applies a Long Short-Term Memory layer to the input. Supported for DQN and PPO agents. |
Note
The bilstmLayer
and batchNormalizationLayer layers are not supported for reinforcement
learning. Normalization in any of the input layers is also not supported.
The Reinforcement Learning Toolbox software provides the following layers, which contain no tunable parameters (that is, parameters that change during training).
| Reinforcement Learning Toolbox Layer | Description |
|---|---|
scalingLayer | Applies a linear scale and bias to an input array. This layer is useful for
scaling and shifting the outputs of nonlinear layers, such as tanhLayer and sigmoidLayer. |
quadraticLayer | Creates a vector of quadratic monomials constructed from the elements of the input array. This layer is useful when you need an output that is some quadratic function of its inputs, such as for an LQR controller. |
softplusLayer | Implements the softplus activation Y = log(1 + eX), which ensures that the output is always positive. This function is a smoothed version of the rectified linear unit (ReLU). |
You can also create your own custom layers. For more information, see Define Custom Deep Learning Layers.
When you create a deep neural network, it is good practice to specify names for the first layer of each input path and the final layer of the output path. These names allow you to connect network paths and then later explicitly associate each network input layer with its appropriate environment channel.
The following code creates and connects the following input and output paths:
An observation input path,
observationPath, with the first layer named"obsInputLayer".An action input path,
actionPath, with the first layer named"actInputLayer".An estimated value function output path,
commonPath, which takes the outputs ofobservationPathandactionPathas inputs and joins them together along the first dimension usingconcatenationLayer. The final layer of this path is named"QValueOutputLayer".
Note
Instead of using concatenationLayer to join the paths, you can also
add the outputs of the previous paths together using additionLayer.
While concatenation and addition both successfully merge paths, the concatenation layer
- everything else equal - uses a larger dimensionality signal after the merging and
thereby involves more learnable parameters and allows more degrees of freedom for the
network to learn the underlying function. Indeed, while an addition layer might need
some preprocessing of its inputs to approximate a desired function, when using a
concatenation layer you can potentially move much of the processing after the
concatenation.
% Observation path: array of layer objects observationPath = [ featureInputLayer(4,Name="obsInputLayer") fullyConnectedLayer(24) reluLayer fullyConnectedLayer(24,Name="ObsFC2") ]; % Action path: array of layer objects actionPath = [ featureInputLayer(1,Name="actInputLayer") fullyConnectedLayer(24,Name="ActFC1") ]; % Common path: array of layer objects commonPath = [ concatenationLayer(1,2,Name="cct") reluLayer fullyConnectedLayer(1,Name="QValueOutputLayer") ]; % Assemble dlnetwork object criticNetwork = dlnetwork(); criticNetwork = addLayers(criticNetwork,observationPath); criticNetwork = addLayers(criticNetwork,actionPath); criticNetwork = addLayers(criticNetwork,commonPath); % Connect layers criticNetwork = connectLayers(criticNetwork,"ObsFC2","cct/in1"); criticNetwork = connectLayers(criticNetwork,"ActFC1","cct/in2"); % Initialize dlnetwork object criticNetwork = initialize(criticNetwork); % Display the number of learnable parameters summary(criticNetwork)
For all observation and action input paths, you must specify a
featureInputLayer as the first layer in the path, with a number of
input neurons equal to the number of dimensions of the corresponding environment
channel.
You can view the structure of your deep neural network using the
plot function.
plot(criticNetwork)
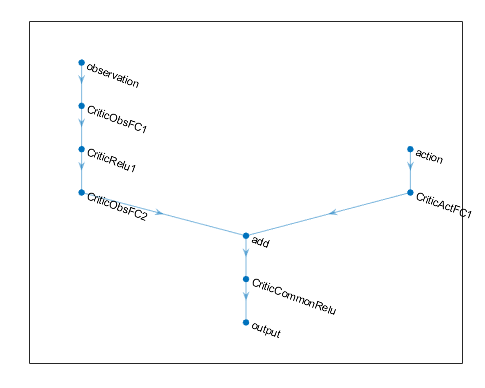
Since the output of a network in an rlDiscreteCategoricalActor actors must represent the probability of executing
each possible action, the software automatically adds a softmaxLayer as
a final output layer if you do not specify it explicitly. When computing the action, the
actor then randomly samples the distribution to return an action.
Determining the number, type, and size of layers for your deep neural network can be difficult and is application dependent. However, the most critical component in deciding the characteristics of the function approximator is whether it is able to approximate the optimal policy or discounted value function for your application, that is, whether it has layers that can correctly learn the features of your observation, action, and reward signals.
Consider the following tips when constructing your network.
For continuous action spaces, bound actions with a
tanhLayerfollowed by aScalingLayerto scale the action to desired values, if necessary.Deep dense networks with
reluLayerlayers can be fairly good at approximating many different functions. Therefore, they are often a good first choice.Start with the smallest possible network that you think can approximate the optimal policy or value function.
When you approximate strong nonlinearities or systems with algebraic constraints, adding more layers is often better than increasing the number of outputs per layer. In general, the ability of the approximator to represent more complex (compositional) functions grows only polynomially in the size of the layers, but grows exponentially with the number of layers. In other words, more layers allow approximating more complex and nonlinear compositional functions, although this generally requires more data and longer training times. Given a total number of neurons and comparable approximation tasks, networks with fewer layers can require exponentially more units to successfully approximate the same class of functions, and might fail to learn and generalize correctly.
For on-policy agents (the ones that learn only from experience collected while following the current policy), such as AC and PG agents, parallel training works better if your networks are large (for example, a network with two hidden layers with 32 nodes each, which has a few hundred parameters). On-policy parallel updates assume each worker updates a different part of the network, such as when they explore different areas of the observation space. If the network is small, the worker updates can correlate with each other and make training unstable.
Create and Configure Actors and Critics from a Neural Network
To create a critic from your deep neural network, use an rlValueFunction,
rlQValueFunction or
(whenever possible) an rlVectorQValueFunction object. To create a deterministic actor for a
continuous action space from your deep neural network, use an rlContinuousDeterministicActor object. To create a stochastic actor from your
deep neural network use either an rlDiscreteCategoricalActor or an rlContinuousGaussianActor object. To configure the learning rate and
optimization used by the actor or critic, use an optimizer object within an agent option
object.
For example, create a Q-value function critic using the neural network
criticNetwork and the environment action and observation
specifications. Pass as additional arguments also the names of the network input layers to
be connected with the observation and action channels, respectively.
critic = rlQValueFunction(criticNetwork,obsInfo,actInfo,... ObservationInputNames={"obsInputLayer"}, ... ActionInputNames="actInputLayer");
To specify training options for the critic, use rlOptimizerOptions
to create the critic optimizer object criticOpts, specifying a learning
rate of 0.02 and a gradient threshold of 1.
criticOpts = rlOptimizerOptions(LearnRate=0.02,...
GradientThreshold=1);Then create an agent option object, and set the
CriticOptimizerOptions property of the agent option object to
criticOpts. When finally you create the agent, pass the agent option
object as a last input argument to the agent constructor function. Alternatively, you can
create the agent first, and then access its option object, and modify the options, using
dot notation.
When you create your deep neural network and configure your actor or critic, consider using the following approach as a starting point.
Start with the smallest possible network and a high learning rate (
0.01). Train this initial network to see if the agent converges quickly to a poor policy or acts in a random manner. If either of these issues occur, rescale the network by adding more layers or more outputs on each layer. Your goal is to find a network structure that is just big enough, does not learn too fast, and shows signs of learning (an improving trajectory of the reward graph) after an initial training period.Once you settle on a good network architecture, a low initial learning rate can allow you to see if the agent is on the right track, and help you check that your network architecture is satisfactory for the problem. A low learning rate makes tuning parameters easier, especially for difficult problems.
Also, consider the following tips when configuring your deep neural network agent.
Be patient with DDPG and DQN agents, since they might not learn anything for some time during the early episodes, and they typically show a dip in cumulative reward early in the training process. Eventually, they can show signs of learning after the first few thousand episodes.
For DDPG and DQN agents, promoting exploration of the agent is critical.
For agents with both actor and critic networks, set the initial learning rates of both actor and critic to the same value. However, for some problems, setting the critic learning rate to a higher value than that of the actor can improve learning results.
Recurrent Neural Networks
When creating actors or critics for use with any agent except Q, SARSA, TRPO and MBPO,
you can use recurrent neural networks (RNN). These networks are deep neural networks with
a sequenceInputLayer input layer and at least one layer that has hidden state
information, such as an lstmLayer. They
can be especially useful when the environment has states that cannot be included in the
observation vector.
For agents that have both actor and critic, you must either use an RNN for both of them, or not use an RNN for any of them. You cannot use an RNN only for the critic or only for the actor.
Note
Code generation is not supported for continuous action space PG, AC, PPO agents, and SAC agents using a recurrent neural network (RNN), or for any agent having multiple input paths and containing an RNN in any of the paths.
When using PG agents, the learning trajectory length (that is the sequence of input
data that the network uses for learning) for the RNN is the whole episode. For an AC
agent, the NumStepsToLookAhead property of its options object is
treated as the training trajectory length (except when training in parallel, in which case
NumStepsToLookAhead is ignored and the whole episode is used as
trajectory length). For a PPO agent, the trajectory length is the
MiniBatchSize property of its options object.
For DQN, DDPG, SAC and TD3 agents, you must specify the trajectory length as an
integer greater than one in the SequenceLength property of their
options object. These learning algorithms randomly sample
MiniBatchSize experience points from all the available episodes.
For each experience point, a sequence of SequenceLength consecutive
experiences is used for learning. If the number of available consecutive experiences is
shorter than SequenceLength (this can happen for example when an
episode terminates prematurely), then the available experiences are padded to complete the
sequence. The sequence is also appropriately masked so that the padded data does not
affect the gradient computation.
For more information and examples on policies and value functions, see rlValueFunction,
rlQValueFunction,
rlVectorQValueFunction, rlContinuousDeterministicActor, rlDiscreteCategoricalActor, and rlContinuousGaussianActor.
Create Built-In Agent from Actor and Critic
Once you create your actor and critic, you can create a built-in reinforcement learning agent that uses them. For example, create a PG agent using a given actor and critic (baseline) network.
agentOpts = rlPGAgentOptions(UseBaseline=true); agent = rlPGAgent(actor,baseline,agentOpts);
For more information on the different types of reinforcement learning agents, see Reinforcement Learning Agents.
You can obtain the actor and critic from an existing agent using getActor and
getCritic,
respectively.
You can also set the actor and critic of an existing agent using setActor and
setCritic,
respectively. The input and output layers of the actor and critic must match the observation
and action specifications of the original agent.
See Also
Functions
Objects
rlTable|rlValueFunction|rlQValueFunction|rlVectorQValueFunction|rlContinuousDeterministicActor|rlDiscreteCategoricalActor|rlContinuousGaussianActor|rlMaxQPolicy|rlEpsilonGreedyPolicy|rlDeterministicActorPolicy|rlAdditiveNoisePolicy|rlStochasticActorPolicy
Related Examples
- Train AC Agent to Balance Cart-Pole System
- Train PG Agent with Baseline to Control Discrete Action Space System
