Design and Analysis of Hairpin Micro-Strip Line Bandpass Filter
This example shows how to design and analyze Hairpin filter in RF PCB Toolbox™.
Most wireless applications require high quality, low cost, and compact sized RF or microwave filters. Planar filters can be used to fulfill this purpose. Among planar filters hairpin filters are available in reduced size as compared to parallel coupled line structures. These hairpin filters may conceptually be obtained by folding the resonators of parallel-coupled half-wavelength resonator filters. The Hairpin filters are widely used as bandpass filters in transmitters and receivers at various frequencies.
Create Variables
N = 3; Ripple = 0.1; BandWidth = 20; Z0 = 50; f = linspace(1.5e9,2.5e9,51); EpsilonR = 6.15; Height = 1.27e-3;
Tapped-Input Hairpin Filter
Use the filterHairpin object to create the hairpin filter and visualize it.
filter = filterHairpin; figure; show(filter); view(-37,30);

Use the design function to design a 3rd order hairpin filter with a RippleFactor of 0.1 dB and 20% fractional bandwidth and visualize it.
filter.FilterOrder = N; filter.Height = Height; filter.Substrate.EpsilonR = EpsilonR; filter = design(filter,2e9,'FBW',BandWidth,'RippleFactor',Ripple); figure; show(filter); view(-37,35);

Use the sparameters function to calculate the s-parameters for the hairpin filter and plot it using rfplot function.
spar = sparameters(filter,f); figure; rfplot(spar);

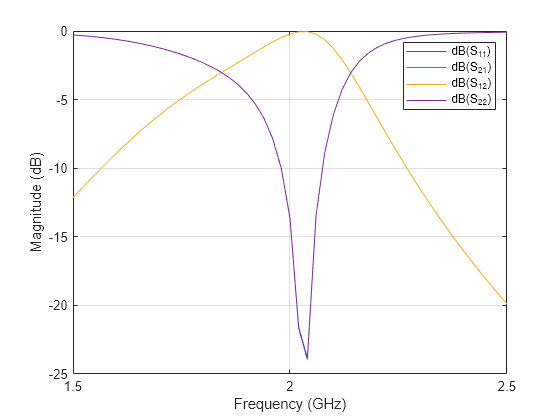
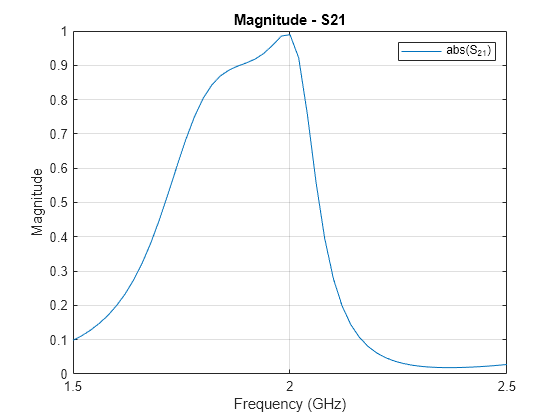
The result shows that the filter resonates close to the design frequency of 2 GHz. The design function uses analytical equations and the spacing between the resonators is generally calculated using the practical approach. Hence the design function sets the spacing to 0.5 mm between all the resonators. To get the accurate results, the spacing between the resonators needs to be adjusted. Increase the bandwidth of the filter by reducing the spacing between the resonators.
Set the Spacing between the resonators to 0.05 mm.
filter.Spacing = [0.05e-3 0.05e-3];
Use the sparameters function to calculate the s-parameters for the hairpin filter and plot it using rfplot function.
spar = sparameters(filter,f); figure; rfplot(spar);
Shifting Resonators and Feed Lines
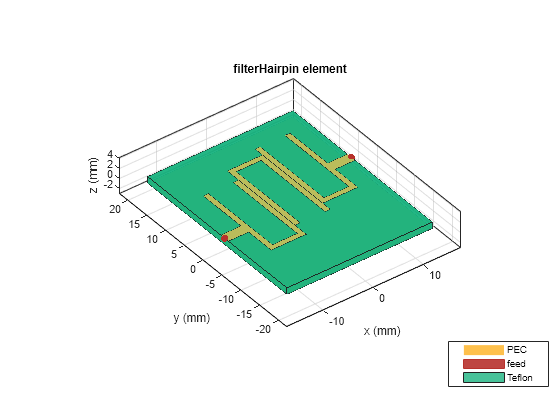
You can also shift the resonators and the feeds using the ResonatorOffset and FeedOffset properties of filterHairpin.
Change the ResonatorOffset and FeedOffset and visualize it.
filter.ResonatorOffset = [0e-3 3e-3 5e-3]; filter.FeedOffset(2) = filter.FeedOffset(2) + 5e-3; figure; show(filter); view(-37,37);
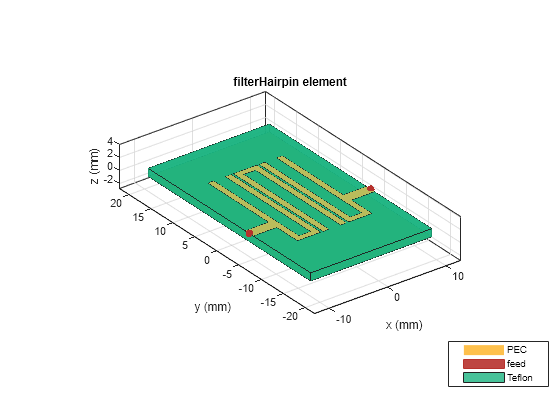
Comparing Results with the Paper
Change the dimensions of the filter as given in [1]. Change the spacing on the filterHairpin and set the spacing to 0.4 mm and set the length of the U-Shaped resonator to 2 mm.
filter.ResonatorOffset = [0e-3 0e-3 0e-3]; filter.Resonator(1).Length(1) = 20.4e-3; filter.Resonator(1).Length(2) = 2e-3; filter.Resonator(1).Length(3) = 20.4e-3; filter.Spacing = [0.4e-3 0.4e-3]; filter.PortLineWidth = 1.85e-3; filter.FeedOffset = [-4.565e-3 -4.565e-3]; figure; show(filter); view(-37,29);
Use the sparameters function to calculate the s-parameters for the hairpin filter and plot it using rfplot function.
spar = sparameters(filter,f);
figure;
rfplot(spar);
title('S-Paramters for the Hairpin Filter');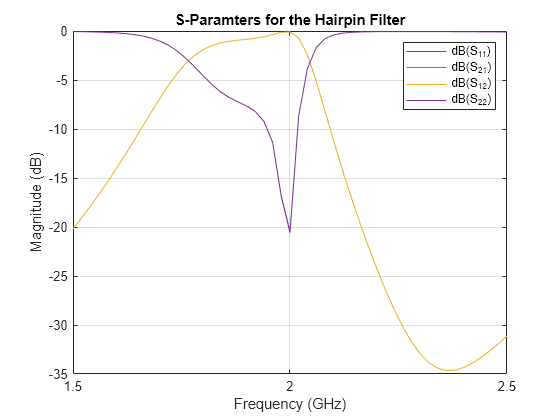
Plot the absolute values of S21 over the frequency range using rfplot function.
figure; rfplot(spar,2,1,'abs'); title('Magnitude - S21');
Coupled-Input Hairpin Filter
Use the filterHairpin object to create the hairpin filter. Change the FeedType property to Coupled to create the hairpin filter with a coupled Input.
filterC = filterHairpin;
filterC.FeedType = 'Coupled';
filterC.FeedOffset = [0 0];
figure;
show(filterC);
view(-37,35);
Use the sparameters function to calculate the s-parameters for the hairpin filter and plot it using rfplot function. The frequency range for the simulation is taken as 1.5 GHz to 2.5 GHz with 301 points. As this below simulation takes more time to run, load the sparameters from the s2p file and then plot the S-Parameters.
sparC = sparameters('sparams.s2p');
figure;
rfplot(sparC);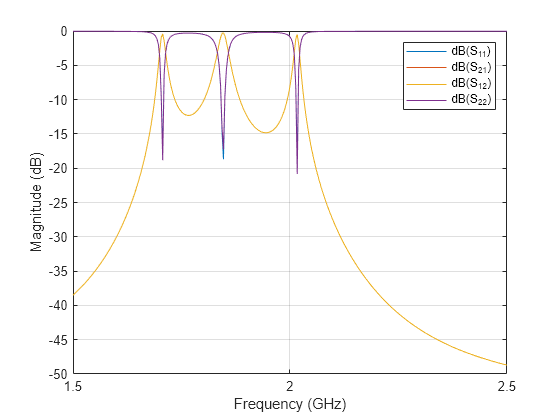
The result shows narrow band resonances at 1.7 GHz, 1.85 GHz, and 2 GHz. For this type of Input, the ResonatorOffset and FeedOffset can be used to create different types of Hairpin Filters.
References
Nikunj Parikh , Pragya Katare , Ketan Kathal , Nandini Patel , Gaurav Chaitanya, Design and Analysis of Hairpin Micro-Strip Line Band Pass Filter.