Main Content

Compare Concentration Indices for Random Portfolios

Open Live Script

This example shows how to simulate random portfolios with different distributions and compare their concentration indices. For illustration purposes, a lognormal and Weibull distribution are used. The distribution parameters are chosen arbitrarily to get a similar range of values for both random portfolios.

Generate random portfolios with different distributions. 

rng('default'); % for reproducibility
PLgn = lognrnd(1,1,1,300);
PWbl = wblrnd(2,0.5,1,300);

Display largest simulated loan value. 

fprintf('\nLargest loan Lognormal: %g\n',max(PLgn));
Largest loan Lognormal: 97.3582

fprintf('Largest loan Weibull: %g\n',max(PWbl));
Largest loan Weibull: 91.5866

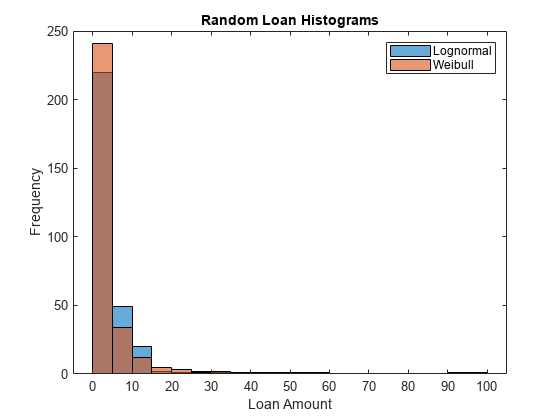
Plot the portfolio histograms. 

figure;
histogram(PLgn,0:5:100)
hold on
histogram(PWbl,0:5:100)
hold off
title('Random Loan Histograms')
xlabel('Loan Amount')
ylabel('Frequency')
legend('Lognormal','Weibull')

Figure contains an axes object. The axes object with title Random Loan Histograms, xlabel Loan Amount, ylabel Frequency contains 2 objects of type histogram. These objects represent Lognormal, Weibull.

Compute and display the concentration measures. 

ciLgn = concentrationIndices(PLgn,'ID','Lognormal');
ciWbl = concentrationIndices(PWbl,'ID','Weibull');
disp([ciLgn;ciWbl])
        ID            CR                                                                          Deciles                                                                        Gini         HH          HK           HT          TE   
    ___________    ________    _____________________________________________________________________________________________________________________________________________    _______    ________    _________    _________    _______

    "Lognormal"    0.066363    0     0.0092101      0.027425      0.053898      0.093295       0.14165       0.20292       0.28269       0.39183       0.55181             1     0.5686    0.013298    0.0045765    0.0077267    0.66735
    "Weibull"      0.090152    0    0.00036887     0.0031072      0.010104      0.021833       0.04367      0.081361       0.13838       0.24197       0.43317             1    0.72876    0.020197    0.0062594     0.012289     1.0944

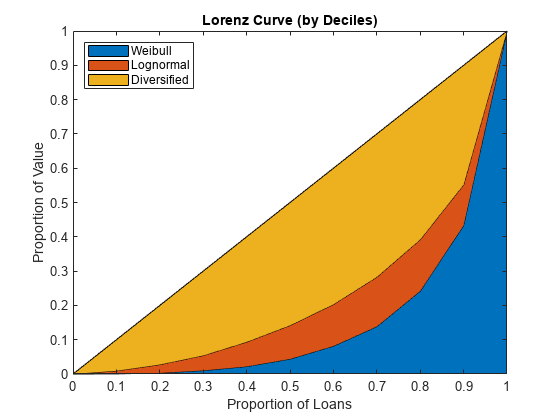
ProportionLoans = 0:0.1:1;
figure;
area(ProportionLoans',[ciWbl.Deciles; ciLgn.Deciles-ciWbl.Deciles; ProportionLoans-ciLgn.Deciles]')
axis([0 1 0 1])
legend('Weibull','Lognormal','Diversified','Location','NorthWest')
title('Lorenz Curve (by Deciles)')
xlabel('Proportion of Loans')
ylabel('Proportion of Value')

Figure contains an axes object. The axes object with title Lorenz Curve (by Deciles), xlabel Proportion of Loans, ylabel Proportion of Value contains 3 objects of type area. These objects represent Weibull, Lognormal, Diversified.

See Also

Related Examples

More About