Row-Major Algorithms for Row-Major Array Layout
This example shows how to use row-major algorithms to generate efficient code. You can enable the Use algorithms optimized for row-major array layout configuration parameter to enable efficient row-major algorithms that are optimized for row-major array layout. The code that you generate by using row-major algorithms performs with better speed and efficient memory usage when operating on data with row-major array layout.
In this example, you operate on row-major data by first using the default column-major algorithms, and then using the row-major algorithms. This comparison helps in identifying the appropriate algorithm settings to achieve different requirements.
Generate Code by Using the Default Column-Major Algorithms for Row-Major Array Layout
Open the example model ex_rowmajor_algorithm.
model = 'ex_rowmajor_algorithm';
open_system(model);
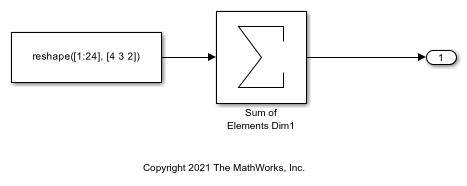
The model contains a Sum of Elements block and the input of the block is an array. By default, Simulink® configures a model with column-major algorithms and column-major array layout. In this example, you configure the array layout of this model as row-major. To specify the array layout, open the Embedded Coder app, and then open the Configuration Parameters dialog box. On the Code Generation > Interface pane, set the configuration parameter Array layout to Row-Major option. Alternatively, in the MATLAB® Command Window, enter:
set_param(model,'ArrayLayout','Row-major');
Generate code from the model by using the slbuild function or by pressing Ctrl+B.
% Generate code and capture the code generation information to Value Value=evalc('slbuild(''ex_rowmajor_algorithm'')');
Inspect the generated ex_rowmajor_algorithm_step step function in the ex_rowmajor_algorithm.c.
file = fullfile('ex_rowmajor_algorithm_ert_rtw','ex_rowmajor_algorithm.c'); coder.example.extractLines(file,'/* Model step function */','/* Model initialize function',1,1);
/* Model step function */
void ex_rowmajor_algorithm_step(void)
{
int32_T i;
int32_T i_0;
int32_T rtb_SumofElementsDim1_tmp;
/* Sum: '<Root>/Sum of Elements Dim1' incorporates:
* Constant: '<Root>/Constant1'
*/
ex_rowmajor_algorithm_Y.Out2 = -0.0F;
for (i = 0; i < 2; i++) {
for (i_0 = 0; i_0 < 3; i_0++) {
rtb_SumofElementsDim1_tmp = (i_0 << 1) + i;
ex_rowmajor_algorithm_Y.Out2 =
(((ex_rowmajor_algorithm_ConstP.Constant1_Value[rtb_SumofElementsDim1_tmp]
+ ex_rowmajor_algorithm_Y.Out2) +
ex_rowmajor_algorithm_ConstP.Constant1_Value[rtb_SumofElementsDim1_tmp
+ 6]) +
ex_rowmajor_algorithm_ConstP.Constant1_Value[rtb_SumofElementsDim1_tmp
+ 12]) +
ex_rowmajor_algorithm_ConstP.Constant1_Value[rtb_SumofElementsDim1_tmp +
18];
}
}
/* End of Sum: '<Root>/Sum of Elements Dim1' */
}
When Array layout is set to Row-major and the Use algorithms optimized for row-major array layout configuration parameter is set to off, the code generator uses column-major algorithms. The algorithms traverse the data in column-major order though the data is in row-major order. This process requires some extra operations in the generated code, which makes the code less efficient. When the Use algorithms optimized for row-major array layout parameter is set to off, the code generator does not include other vectorization optimizations such as single-instance, multiple-data (SIMD) optimizations.
Generate Code by Using the Row-Major Algorithms for Row-Major Array Layout
To enable the row-major algorithms, on the Math & Data Types pane, select the configuration parameter Use algorithms optimized for row-major array layout check box. This parameter enables the algorithms that are optimized for row-major array layout. Alternatively, in the MATLAB Command Window, enter:
set_param(model,'UseRowMajorAlgorithm','on');
After enabling the row-major algorithms, generate code.
Value=evalc('slbuild(''ex_rowmajor_algorithm'')');
Inspect the generated ex_rowmajor_algorithm_step step function in the ex_rowmajor_algorithm.c.
file = fullfile('ex_rowmajor_algorithm_ert_rtw','ex_rowmajor_algorithm.c'); coder.example.extractLines(file,'/* Model step function */','/* Model initialize function',1,1);
/* Model step function */
void ex_rowmajor_algorithm_step(void)
{
int32_T i;
/* Sum: '<Root>/Sum of Elements Dim1' incorporates:
* Constant: '<Root>/Constant1'
*/
ex_rowmajor_algorithm_Y.Out2 = -0.0F;
for (i = 0; i < 24; i++) {
ex_rowmajor_algorithm_Y.Out2 +=
ex_rowmajor_algorithm_ConstP.Constant1_Value[i];
}
/* End of Sum: '<Root>/Sum of Elements Dim1' */
}
When the Array layout is set to Row-major and the Use algorithms optimized for row-major array layout configuration parameter is set to on, the code generator generates efficient code. The code generator uses row-major algorithms that traverse the data in row-major order, which reduces the number of operations in the generated code. However, you might notice a minor numeric difference between the outputs of column-major and row-major algorithms due to the operation order.