Stochastic Simulation of the Lotka-Volterra Reactions

This example shows how to build and simulate a model using the SSA stochastic solver.

The following model will be constructed and stochastically simulated:

Reaction 1: x + y1 -> 2 y1 + x, with rate constant, c1 = 10.
Reaction 2: y1 + y2 -> 2 y2, with rate constant, c2 = 0.01.
Reaction 3: y2 -> z, with rate constant, c3 = 10.
Initial conditions: x=1 (constant), y1=y2=1000, z=0.
Note: Species 'x' in Reaction 1 is represented on both sides of the reaction to model the assumption that the amount of x is constant.

These reactions can be interpreted as a simple predator-prey model if one considers that the prey population (y1) increases in the presence of food (x) (Reaction 1), that the predator population (y2) increases as they eat prey (Reaction 2), and that predators (y2) die of natural causes (Reaction 3).

This example uses parameters and conditions as described in Daniel T. Gillespie, 1977, "Exact Stochastic Simulation of Coupled Chemical Reactions," The Journal of Physical Chemistry, vol. 81, no. 25, pp. 2340-2361.

Register Units for the Model

sbioaddtolibrary(sbiounit('rabbit','molecule',1));
sbioaddtolibrary(sbiounit('coyote','molecule',1));
sbioaddtolibrary(sbiounit('food','molecule',1));
sbioaddtolibrary(sbiounit('amountDimension','molecule',1));

Create the Lotka-Volterra Model

model = sbiomodel('Lotka-Volterra Model');
c = addcompartment(model,'C');
c.CapacityUnits = 'meter^3';

Add Reaction 1 to the Model Object

r1 = addreaction(model,'x + y1 -> 2 y1 + x')

r1 = 
   SimBiology Reaction Array

   Index:    Reaction:         
   1         x + y1 -> 2 y1 + x

% Set the Kinetic Law for Reaction 1.
kl1 = addkineticlaw(r1, 'MassAction');

% Add rate constant parameter, c1, to reaction with value = 10
p1 = addparameter(kl1, 'c1', 'Value', 10);

kl1.ParameterVariableNames = {'c1'};

% Add units to c1
p1.ValueUnits = '1/(second*rabbit)';

% Set initial amounts for species in Reaction 1
r1.Reactants(1).InitialAmount = 1;             % x
r1.Reactants(2).InitialAmount = 1000;          % y1

% Set the initial amount units for species in Reaction 1
r1.Reactants(1).InitialAmountUnits = 'food';   % x
r1.Reactants(2).InitialAmountUnits = 'rabbit'; % y1

Add Reaction 2 to the Model Object

r2 = addreaction(model,'y1 + y2 -> 2 y2')

r2 = 
   SimBiology Reaction Array

   Index:    Reaction:      
   1         y1 + y2 -> 2 y2

% Set the kinetic law for Reaction 2.
kl2 = addkineticlaw(r2, 'MassAction');

% Add rate constant parameter, c2, to kinetic law with value = 0.01
p2 = addparameter(kl2, 'c2', 'Value', 0.01);

kl2.ParameterVariableNames = {'c2'};

% Add units to c2
p2.ValueUnits = '1/(second*coyote)';

% Set initial amounts for new species in Reaction 2
r2.Products(1).InitialAmount = 1000;          % y2
% Set the initial amount units for new species in Reaction 2
r2.Products(1).InitialAmountUnits = 'coyote'; % y2

Add Reaction 3 to the Model Object

r3 = addreaction(model,'y2 -> z')

r3 = 
   SimBiology Reaction Array

   Index:    Reaction:
   1         y2 -> z

% Add "bogus" units to trash variable 'z'
r3.Products(1).InitialAmountUnits = 'amountDimension';

% Set the kinetic law for Reaction 3.
kl3 = addkineticlaw(r3, 'MassAction');

% Add rate constant parameter, c3, to reaction with value = 10
p3 = addparameter(kl3, 'c3', 'Value', 10);

kl3.ParameterVariableNames = {'c3'};

% Add units to c3
p3.ValueUnits = '1/second';

Display the Completed Model Objects

model

model = 
   SimBiology Model - Lotka-Volterra Model 

   Model Components:
     Compartments:      1
     Events:            0
     Parameters:        3
     Reactions:         3
     Rules:             0
     Species:           4
     Observables:       0

Display the Reaction Objects

model.Reactions

ans = 
   SimBiology Reaction Array

   Index:    Reaction:         
   1         x + y1 -> 2 y1 + x
   2         y1 + y2 -> 2 y2   
   3         y2 -> z

Display the Species Objects

model.Species

ans = 
   SimBiology Species Array

   Index:    Compartment:    Name:    Value:    Units:         
   1         C               x        1         food           
   2         C               y1       1000      rabbit         
   3         C               y2       1000      coyote         
   4         C               z        0         amountDimension

Simulate with the Stochastic (SSA) Solver & Plot

cs = getconfigset(model,'active');
cs.SolverType = 'ssa';
cs.StopTime = 30;
cs.SolverOptions.LogDecimation = 200;
cs.CompileOptions.UnitConversion = true;
[t,X] = sbiosimulate(model);

plot(t, X(:,2), t, X(:,3));
legend('Y1', 'Y2');
title('Lotka-Volterra Reaction - State History');
ylabel('Number of predator-prey');
grid on;

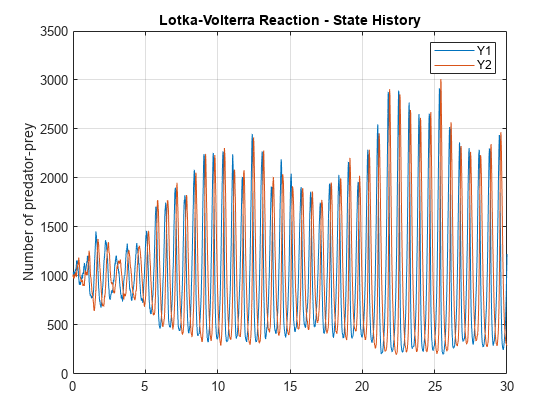
Figure contains an axes object. The axes object with title Lotka-Volterra Reaction - State History, ylabel Number of predator-prey contains 2 objects of type line. These objects represent Y1, Y2.

Show Phase Portrait of Y1 to Y2

plot(X(:,2),X(:,3));
title('Lotka-Volterra Reaction - Y1 vs. Y2');
xlabel('Number of Y1 rabbits');
ylabel('Number of Y2 coyotes');

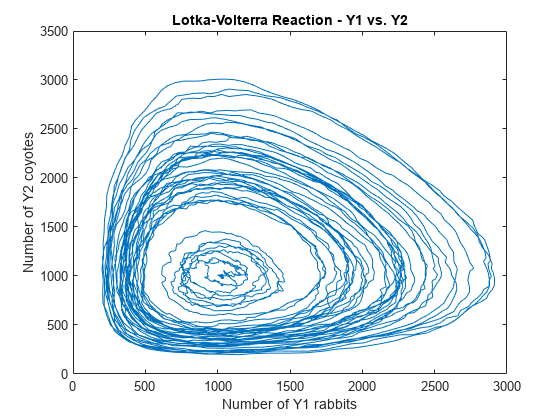
Figure contains an axes object. The axes object with title Lotka-Volterra Reaction - Y1 vs. Y2, xlabel Number of Y1 rabbits, ylabel Number of Y2 coyotes contains an object of type line.

% Clean up units.
sbioremovefromlibrary('unit', 'rabbit');
sbioremovefromlibrary('unit', 'coyote');
sbioremovefromlibrary('unit', 'food');
sbioremovefromlibrary('unit', 'amountDimension');