Dining Philosophers Problem

Problem Description

The Dining Philosophers problem is a classical problem, originally formulated by E.W. Dijkstra, to demonstrate classical problems in computer science and the programming of concurrent or parallel processes.

Four philosophers are seated at a table, spending their lives in an infinite cycle of thinking and eating. A philosopher must pick up both forks before he can eat. You can think of the philosophers as concurrent processes and the forks as shared resources. The problem is to determine the policy or algorithm so that each philosopher gets to eat and does not starve. For example, one algorithm is for each philosopher to pick up first the fork to his right, then the fork to his left, before he eats. That this will eventually lead to a deadlock situation where all of the philosophers are holding one fork, waiting for each other to put down their forks.

Philosopher Model

This example models each philosopher as a discrete event system that generates a single entity at the start of the simulation. The position of the entity within the system reflects the state of the philosopher. Each state of the philosopher is an Entity Server that can hold the entity for a randomized period of time.

Resource Hierarchy Solution

The algorithm illustrated here is a variation of the original algorithm described by Dijkstra. Each fork is numbered and philosophers first pick up the smaller numbered fork and then the larger numbered fork. This algorithm is sufficient to avoid deadlocks because only one philosopher can ever hold the highest numbered fork and consequently that philosopher can proceed to eat.

Results

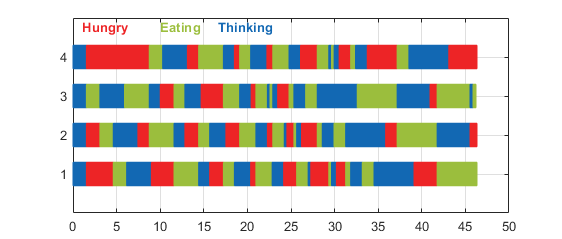
The first figure shows a Gantt chart of all four philosophers as they cycle between thinking, starving, and eating.

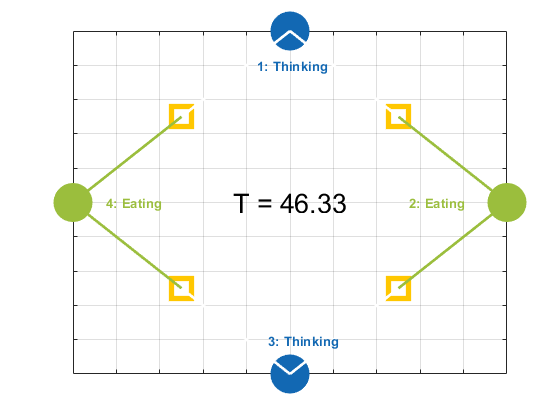
The second figure shows the instantaneous states of all four philosophers during the simulation. A line drawn from a philosopher (filled circle) to a fork (rounded rectangle) indicates that the philosopher has picked up that fork and hence the fork is unavailable for its neighbor.

Deadlock

In this model, a deadlock can be reached if Philosopher 4 reverses his order of fork preference so that he picks up Fork 4 before Fork 1. This violates the above resource hierarchy constraint and simulating the model with this change will result in a deadlock as shown below.

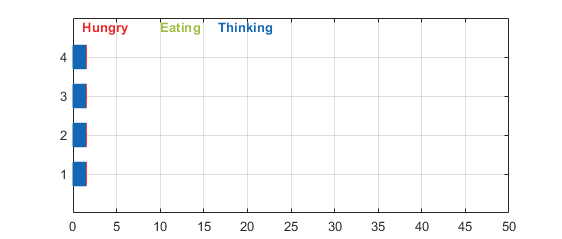
The result above shows that each philosopher has picked up the right fork and everyone is waiting for the other fork to become available, causing a deadlock.

References

[1] Dining Philosophers Problem - Wikipedia (https://en.wikipedia.org/wiki/Dining_philosophers_problem)