Main Content

Modulate Input Signal onto Square Carrier Wave

Open Script

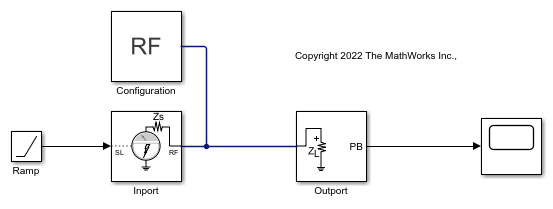
Use the Inport block to modulate an input signal onto a square carrier wave in the circuit envelope simulation environment.

Open the model and double-click the Inport block to set the parameters as follows.

  • Source type — power

  • Source impedance (Ohm) — 50

  • Carrier frequencies — 3e9 Hz

  • Use square wave — on

  • Number of Fourier Coefficients — 15

  • DC Bias — – 0.5

  • Duty Cycle (%) — 50

  • Ground and hide negative terminals — on

Run the model and view the result in the scope.

Double-click the Inport block and select the View button to plot the simulation frequencies for the square carrier wave and the approximate square wave with RSM error of the approximation.

Change the DC Bias value to 0, press Apply, and then press View again. The DC coefficient has increased and the Carrier wave function is between 0 and 1.

Run the model. The scope now shows that the modulated square wave is alternating between 0 and the ramp envelope.

In the Inport block, change the Number of Fourier Coefficients from 15 to 30. Press Apply and select the View button to see the effect on the expected square wave.

The calculated RMS Error is down from 0.085 to 0.0581.

Double-click the Outport block to open its mask and change the value of the Carrier frequencies parameter from 3e9*[0:15-1] to 3e9*[0:30-1]. Rerun the model to view the change to the output signal in the scope. The ripples are now denser and smaller (except for the expected Gibbs effect at the discontinuities) with more Fourier coefficients to approximate the square wave.

You can also try:

  • Changing the Number of Fourier coefficients, DC Bias, and Duty Cycle parameters to different values to view the effect on the visualization plot and output.

  • Changing the Ramp block to another function to represent a different envelope.

  • Changing the RF system (for example, adding a nonlinear amplifier) and output complex baseband signals. The input square wave is created without RMS normalization, so the peak values correspond to the Fourier coefficients, while the output complex baseband are RMS normalized, and the values at the output are expected to be 1/sqrt(2) smaller than the Fourier coefficients seen in the visualization plot.

See Also

Related Topics