Battery Capacity Estimator (Least Squares)

Battery capacity estimator using least-squares algorithms

Since R2024a

Libraries:
Simscape / Battery / BMS / Estimators

Description

The Battery Capacity Estimator (Least Squares) block calculates the cell capacity of a battery by using least-squares algorithms.

For discrete-time simulation, set the Sample time parameter to a positive value. To inherit the sample time, set Sample time to -1. For continuous-time simulation, set Sample time to 0.

Equations

The least-squares estimation finds the line of best fit for a set of data points by minimizing the sum of the squared residuals. The squared residuals are the difference between the observed responses and the predicted responses of the model. This line of best fit predicts the dependent variable.

This equation defines the battery state of charge (SOC) at time t_n2,

$S O C (t_{n2}) = S O C (t_{n1}) + \frac{1}{Q} \int_{t_{n1}}^{t_{n2}} i (τ) d τ,$

where:

SOC(t_n1) is the SOC at time t_n1, with n={1,…,N}.
Q is the capacity in ampere-hours.
i is the battery cell current in amperes.
$\int_{t_{n1}}^{t_{n2}} i (τ) d τ$ denotes the integrated battery cell current over the time interval t_n2 - t_n1. Time t_n1 and t_n2 must be in hours for the units to be consistent.

Define $x_{n} = S O C (t_{n2}) - S O C (t_{n1})$ and $y_{n} = \int_{t_{n1}}^{t_{n2}} i (τ) d τ$ , and rewrite the SOC equation:

$y_{n} = Q x_{n} .$

The block uses this linear equation to determine an estimate of the cell capacity using the least squares estimation,

$(y_{n} - Δ y_{n}) = \hat{Q} (x_{n} - Δ x_{n}),$

where:

Δx_n is the error associated with the SOC estimation.
Δy_n is the error associated with the current sensor.
$\hat{Q}$ is an estimate of the true cell capacity under noisy measurements.

Ordinary Least Squares

The weighted ordinary least squares (OLS) method estimates the cell capacity by minimizing the weighted squared errors, Δy_n, of the merit function

$x_{WLS}^{2} = \sum_{n = 1}^{N} \frac{{(y_{n} - Y_{n})}^{2}}{σ_{yn}^{2}} = \sum_{n = 1}^{N} \frac{{(y_{n} - \hat{Q} x_{n})}^{2}}{σ_{yn}^{2}},$

where σ²_yn denotes the variance of the current measurement and Y_n is a point on the line $Y_{n} = \hat{Q} x_{n}$ that corresponds to the measurement data point {x_n,y_n}. The block assumes that y_n has noise and x_n has no noise.

To solve the weighted OLS problem, the block differentiates the merit function with respect to $\hat{Q}$ and solves for $\hat{Q}$ by setting the partial derivative to zero [1]:

$\begin{matrix} \frac{\partial x_{WLS}^{2}}{\partial \hat{Q}} = - 2 \sum_{n = 1}^{N} \frac{x_{n} (y_{n} - \hat{Q} x_{n})}{σ_{yn}^{2}} = 0 \\ \hat{Q} \sum_{n = 1}^{N} \frac{x_{n}^{2}}{σ_{yn}^{2}} = \sum_{n = 1}^{N} \frac{x_{n} y_{n}}{σ_{yn}^{2}} \\ \hat{Q} = \frac{\sum_{n = 1}^{N} \frac{x_{n} y_{n}}{σ_{yn}^{2}}}{\sum_{n = 1}^{N} \frac{x_{n}^{2}}{σ_{yn}^{2}}} \end{matrix}$

This method can be computed recursively and is easily adapted to allow fading of past measurements.

If you define the forgetting factor as $0 ≪ γ \leq 1$ , then the block obtains the estimated capacity from the equation

$\hat{Q} = \frac{k_{2, n}}{k_{1, n}},$

where:

$\begin{array}{l} k_{1, n} = γ k_{1, n - 1} + \frac{x_{n}^{2}}{σ_{yn}^{2}} \\ k_{2, n} = γ k_{2, n - 1} + \frac{x_{n} y_{n}}{σ_{yn}^{2}} \end{array}$

Total Least Squares

The weighted total least squares (TLS) method estimates the cell capacity by minimizing the sum of both weighted square errors, Δx_n and Δy_n, of the merit function [1],[2],

$χ_{WLTS}^{2} = \sum_{n = 1}^{N} \frac{{(y_{n} - Y_{n})}^{2}}{σ_{yn}^{2}} + \frac{{(x_{n} - X_{n})}^{2}}{σ_{xn}^{2}},$

where σ²_yn denotes the variance of the current measurement, σ²_xn denotes the variance of the error on the SOC estimates, and X_n and Y_n are points on the line $Y_{n} = \hat{Q} X_{n}$ that corresponds to the noisy measured data point {x_n,y_n}.

To enforce $Y_{n} = \hat{Q} X_{n}$ , the block augments the merit function with Lagrange multipliers λ_i:

$χ_{WLTS, a}^{2} = \sum_{n = 1}^{N} \frac{{(y_{n} - Y_{n})}^{2}}{σ_{yn}^{2}} + \frac{{(x_{n} - X_{n})}^{2}}{σ_{xn}^{2}} - λ_{i} (Y_{n} - \hat{Q} X_{n}) .$

The block sets the partial derivatives of $χ_{WLTS, a}^{2}$ with respect to λ_i, Y_n, and X_n to zero:

$\begin{matrix} \frac{\partial χ_{WLTS, a}^{2}}{\partial λ_{i}} = - (Y_{n} - \hat{Q} X_{n}) = 0 \to Y_{n} = \hat{Q} X_{n} \\ \frac{\partial χ_{WLTS, a}^{2}}{\partial Y_{n}} = \frac{- 2 (y_{n} - Y_{n})}{σ_{yn}^{2}} - λ_{i} = 0 \to λ_{i} = \frac{- 2 (y_{n} - Y_{n})}{σ_{yn}^{2}} \\ \frac{\partial χ_{WLTS, a}^{2}}{\partial X_{n}} = \frac{- 2 (x_{n} - X_{n})}{σ_{xn}^{2}} + λ_{i} \hat{Q} = 0 \to X_{n} = \frac{x_{n} σ_{y n}^{2} + \hat{Q} y_{n} σ_{x n}^{2}}{σ_{y n}^{2} + {\hat{Q}}^{2} σ_{x n}^{2}} \end{matrix}$

Then the block rewrites the merit function as [1]:

$χ_{WLTS}^{2} = \sum_{n = 1}^{N} \frac{{(y_{n} - Y_{n})}^{2}}{σ_{yn}^{2}} + \frac{{(x_{n} - X_{n})}^{2}}{σ_{xn}^{2}} = \sum_{n = 1}^{N} \frac{{(y_{n} - \hat{Q} x_{n})}^{2}}{σ_{yn}^{2} + {\hat{Q}}^{2} σ_{xn}^{2}} .$

Finally, the block sets the partial derivative of $χ_{WLTS}^{2}$ with respect to $\hat{Q}$ to zero:

$\frac{\partial χ_{WLTS}^{2}}{\partial \hat{Q}} = \sum_{n = 1}^{N} \frac{2 (\hat{Q} x_{n} - y_{n}) (\hat{Q} y_{n} σ_{xn}^{2} + x_{n} σ_{yn}^{2})}{{({\hat{Q}}^{2} σ_{xn}^{2} + σ_{yn}^{2})}^{2}} = 0.$

In this equation:

There is no closed-form solution in the general case. To find a closed-form solution, perform a Newton-Raphson search for $\hat{Q}$ .
There is no recursive update in the general case.
The solution is impractical for implementation in an embedded system.

Recursive Approximation of Total Least Squares (RTLS)

The block substitutes $σ_{xn} = k σ_{yn}$ in the equation of $χ_{WLTS}^{2}$ :

$χ_{RTLS}^{2} = \sum_{n = 1}^{N} \frac{{(y_{n} - Y_{n})}^{2}}{σ_{yn}^{2}} + \frac{{(x_{n} - X_{n})}^{2}}{k σ_{yn}^{2}} = \sum_{n = 1}^{N} \frac{{(y_{n} - \hat{Q} x_{n})}^{2}}{({\hat{Q}}^{2} k^{2} + 1) σ_{yn}^{2}} .$

The partial derivative of the WTLS merit function reduces to:

$\begin{matrix} \frac{\partial χ_{RTLS}^{2}}{\partial \hat{Q}} = 2 \sum_{n = 1}^{N} \frac{(\hat{Q} x_{n} - y_{n}) (\hat{Q} k^{2} y_{n} + x_{n})}{{({\hat{Q}}^{2} k^{2} + 1)}^{2} σ_{yn}^{2}} = 0 \\ {\hat{Q}}^{2} \underset{a}{\underset{︸}{\sum_{n = 1}^{N} k^{2} \frac{x_{n} y_{n}}{σ_{yn}^{2}}}} + \underset{b}{\underset{︸}{\sum_{n = 1}^{N} k^{2} \frac{x_{n}^{2} - k^{2} y_{n}^{2}}{σ_{yn}^{2}}}} + \underset{c}{\underset{︸}{\sum_{n = 1}^{N} \frac{- x_{n} y_{n}}{σ_{yn}^{2}}}} = 0 \\ \hat{Q} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \end{matrix}$

The block incorporates fading memory by using this equation

$\hat{Q} = \frac{- k_{1, n} + k^{2} k_{3, n} + \sqrt{{(k_{1, n} - k^{2} k_{3, n})}^{2} + 4 k^{2} k_{2, n}^{2}}}{2 k^{2} k_{2, n}},$

where:

$\begin{matrix} k_{1, n} = γ k_{1, n - 1} + \frac{x_{n}^{2}}{σ_{yn}^{2}} \\ k_{2, n} = γ k_{2, n - 1} + \frac{x_{n} y_{n}}{σ_{yn}^{2}} \\ k_{3, n} = γ k_{3, n - 1} + \frac{y_{n}^{2}}{σ_{yn}^{2}} \end{matrix}$

Approximate Total Least Squares (ATLS)

The ATLS method is recursive and allows σ²_yn and σ²_xn to be non-proportional.

This figure shows the definitions the block uses to derive the approximate weighted total least squares:

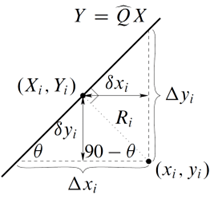
The block defines Δx_n and Δy_n as the x-distance and y-distance between the data point n and the line, respectively. The slope of the line is $\hat{Q} = \frac{Δ y_{n}}{Δ x_{n}}$ for all n. The angle of the line is $θ = \tan^{- 1} \hat{Q} .$

This equation defines the shortest distance between the line and a given data point:

$R_{n} = Δ y_{n} \cos θ = \frac{Δ y_{n}}{\sqrt{1 + {\hat{Q}}^{2}}} .$

If $δ x_{i} = R_{i} \sin θ$ and $δ y_{i} = R_{i} \cos θ$ , the block defines the x and y components of the perpendicular distance between the data point n and the fitting line. Then the block can define the AWTLS merit function using this equation:

$χ_{AWTLS}^{2} = \sum_{n = 1}^{N} \frac{δ x_{n}^{2}}{σ_{xn}^{2}} + \frac{δ y_{n}^{2}}{σ_{yn}^{2}} = \sum_{n = 1}^{N} \frac{{(y_{n} - \hat{Q} x_{n})}^{2}}{{({\hat{Q}}^{2} + 1)}^{2}} (\frac{{\hat{Q}}^{2}}{σ_{xn}^{2}} + \frac{1}{σ_{yn}^{2}}) .$

This equation defines the Jacobian of the AWTLS merit function:

$\frac{\partial χ_{AWTLS}^{2}}{\partial \hat{Q}} = \frac{2}{{({\hat{Q}}^{2} + 1)}^{3}} \sum_{n = 1}^{N} {\hat{Q}}^{4} \frac{x_{n} y_{n}}{σ_{xn}^{2}} + {\hat{Q}}^{3} (\frac{2 x_{n}^{2}}{σ_{xn}^{2}} - \frac{x_{n}^{2}}{σ_{yn}^{2}} - \frac{y_{n}^{2}}{σ_{xn}^{2}}) + {\hat{Q}}^{2} (\frac{3 x_{n} y_{n}}{σ_{yn}^{2}} - \frac{3 x_{n} y_{n}}{σ_{xn}^{2}}) + \hat{Q} (\frac{x_{n}^{2} - 2 y_{n}^{2}}{σ_{yn}^{2}} + \frac{y_{n}^{2}}{σ_{xn}^{2}}) + \frac{- x_{n} y_{n}}{σ_{yn}^{2}} .$

The roots of the quartic equation are the candidate solutions for $\hat{Q}$ . The block rewrites the quartic equations as

$c_{5, n} {\hat{Q}}^{4} + (2 c_{4, n} - c_{1, n} - c_{6, n}) {\hat{Q}}^{3} + (3 c_{2, n} - 3 c_{5, n}) {\hat{Q}}^{2} + (c_{1, n} - 2 c_{3, n} + c_{6, n}) \hat{Q} - c_{2, n} = 0,$

where:

$\begin{matrix} c_{1, n} = γ c_{1, n - 1} + \frac{x_{n}^{2}}{k^{2} σ_{yn}^{2}} \\ c_{2, n} = γ c_{2, n - 1} + \frac{k x_{n} y_{n}}{k^{2} σ_{yn}^{2}} \\ c_{3, n} = γ c_{3, n - 1} + \frac{y_{n}^{2}}{σ_{yn}^{2}} \\ c_{4, n} = γ c_{4, n - 1} + \frac{x_{n}^{2}}{σ_{xn}^{2}} \\ c_{5,n} = γ c_{5, n - 1} + \frac{k x_{n} y_{n}}{σ_{xn}^{2}} \\ c_{6,n} = γ c_{6, n - 1} + \frac{k^{2} y_{n}^{2}}{σ_{xn}^{2}} \end{matrix}$

The ATLS merit function does not equal the weighted TLS merit function when $σ_{xn} = k σ_{yn}$ .

When $σ_{xn} = k σ_{yn}$ , the block uses this equation to estimate the true cell capacity:

${\hat{Q}}_{corrected} = \frac{\hat{Q}}{k} .$

Implementation

This figure shows how the block estimates the battery capacity using the different least-squares algorithms:

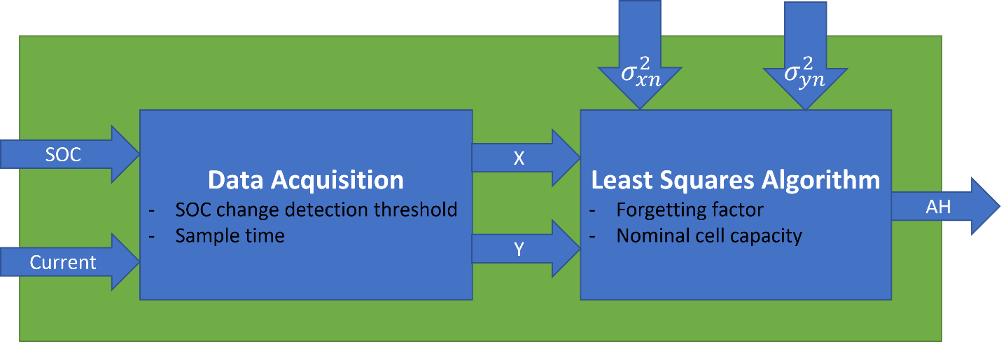
During the Data Acquisition phase, the block runs in a loop until the algorithm finds a valid data point. The block follows these steps:

The block receives an SOC estimate at time t_n1 using an SOC estimator.
The block receives a second SOC estimate at time t_n2.
While $S O C (t_{n 1}) - S O C (t_{n 2}) < S O C_{\min_change}$ , the block:
- Keeps receiving SOC estimates.
- Integrates cell current, $y_{n} = \int_{t_{n1}}^{t_{n2}} i (τ) d τ$ .
- Overwrites time t_n2 with a new timestamp.
- If the battery is charging, the block discards the measurement and goes back to step 1.

Assumptions and Limitations

The block assumes the random errors Δx_n and Δy_n follow a zero-mean normal distribution.
The block assumes that the weights σ²_xn and σ²_yn are known.
In the RTLS algorithm, the scaling factor k must proportionally relate the weights σ²_xn and σ²_yn such that $σ_{xn} = k σ_{yn}$

Ports

Input

expand all

Current — Battery current, A
scalar | vector

Battery current, in amperes, specified as a scalar for a single cell or a vector for multiple cells. To specify this input as a vector of cell currents, select the Specify Current input as cell current(s) parameter. If you select this parameter, the size of this input port must be equal to the size of the other input ports.

CellSOC — Cell state of charge, unitless
scalar | vector

State of charge of one or multiple cells, specified as a scalar or vector of entries in the range [0, 1]. The size of this input port must be equal to the size of the InitialCellAH input port.

InitialCellAH — Cell temperature, A*Hr
scalar | vector

Initial cell capacity of the battery, in ampere-hours, specified as a scalar for a single cell or a vector for multiple cells. The size of this input port must be equal to the size of the CellSOC input port.

Output

expand all

CellAH — Estimated cell capacity, A*Hr
scalar | vector

Estimated cell capacity of the battery, in ampere-hours, returned as a scalar or a vector. The size of this output port is equal to the size of the InitialCellAH input port.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Specify Current input as cell current(s) — Option to specify current input port as vector
`off` (default) | `on`

Option to specify the value of the Current input port as a vector of cell currents. If you select this parameter, the value at the Current input port can be a scalar or a vector of size equal to the size of the block inputs.

Least square algorithm — Least-square algorithm
`Ordinary least squares` (default) | `Recursive total least squares` | `Approximate total least squares`

Least-square algorithm that the block uses to estimate the battery cell capacity.

SOC change detection threshold — Threshold to detect change in SOC
`0.03` (default) | scalar in the range (0,1)

Threshold to detect a change in the SOC. Typical values are 0.05 or 0.03, which represent a 5% or 3% change.

Forgetting factor, gamma — Forgetting factor
`0.9` (default) | scalar in the range (0,1]

Forgetting factor.

Variance of SOC, VarianceX — Variance of SOC
`2e-4` (default) | positive scalar

Variance of the battery SOC.

Dependencies

To enable this parameter, set Least squares algorithm to Approximate total least squares.

Variance of current measurement, VarianceY — Variance of current measurement
`5e-7` (default) | positive scalar

Variance of the current measurement.

**Scaling factor k in VarianceX=k^2*VarianceY** — Scaling factor k
`10` (default) | positive scalar

Scaling factor k.

Dependencies

To enable this parameter, set Least squares algorithm to Recursive total least squares or Approximate total least squares.

Sample time (-1 for inherited) — Block sample time
`1` (default) | `0` | `-1` | positive integer

Time between consecutive block executions. During execution, the block produces outputs and, if appropriate, updates its internal state. For more information, see What Is Sample Time? and Specify Sample Time.

For inherited discrete-time operation, specify this parameter as -1. For discrete-time operation, specify this parameter as a positive integer. For continuous-time operation, specify this parameter as 0.

If this block is in a masked subsystem or a variant subsystem that supports switching between continuous and discrete operations, promote the sample time parameter. Promoting the sample time parameter ensures correct switching between the continuous and discrete implementations of the block. For more information, see Promote Block Parameters on a Mask.

References

[1] Plett, G., Battery Management Systems: Volume II, Equivalent-Circuit Methods, Artech House, 2015.

[2] E. Bakas, B. Rosca, S. Wilkins, T. Donkers. Least-Squares-based Capacity Estimation for Lithium-ion Battery Cells, The European Battery, Hybrid and Fuel Cell Electric Vehicle Congress, Geneva, Switzerland, 2017.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2024a

Battery Capacity Estimator (Least Squares)

Description

Equations

Implementation

Assumptions and Limitations

Ports

Input

Current — Battery current, A scalar | vector

CellSOC — Cell state of charge, unitless scalar | vector

InitialCellAH — Cell temperature, A*Hr scalar | vector

Output

CellAH — Estimated cell capacity, A*Hr scalar | vector

Parameters

Specify Current input as cell current(s) — Option to specify current input port as vector off (default) | on

Least square algorithm — Least-square algorithm Ordinary least squares (default) | Recursive total least squares | Approximate total least squares

SOC change detection threshold — Threshold to detect change in SOC 0.03 (default) | scalar in the range (0,1)

Forgetting factor, gamma — Forgetting factor 0.9 (default) | scalar in the range (0,1]

Variance of SOC, VarianceX — Variance of SOC 2e-4 (default) | positive scalar

Dependencies

Variance of current measurement, VarianceY — Variance of current measurement 5e-7 (default) | positive scalar

Scaling factor k in VarianceX=k^2*VarianceY — Scaling factor k 10 (default) | positive scalar

Dependencies

Sample time (-1 for inherited) — Block sample time 1 (default) | 0 | -1 | positive integer

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Current — Battery current, A
scalar | vector

CellSOC — Cell state of charge, unitless
scalar | vector

InitialCellAH — Cell temperature, A*Hr
scalar | vector

CellAH — Estimated cell capacity, A*Hr
scalar | vector

Specify Current input as cell current(s) — Option to specify current input port as vector
`off` (default) | `on`

Least square algorithm — Least-square algorithm
`Ordinary least squares` (default) | `Recursive total least squares` | `Approximate total least squares`

SOC change detection threshold — Threshold to detect change in SOC
`0.03` (default) | scalar in the range (0,1)

Forgetting factor, gamma — Forgetting factor
`0.9` (default) | scalar in the range (0,1]

Variance of SOC, VarianceX — Variance of SOC
`2e-4` (default) | positive scalar

Variance of current measurement, VarianceY — Variance of current measurement
`5e-7` (default) | positive scalar

**Scaling factor k in VarianceX=k^2*VarianceY** — Scaling factor k
`10` (default) | positive scalar

Sample time (-1 for inherited) — Block sample time
`1` (default) | `0` | `-1` | positive integer

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.