Main Content

Two-Phase Fluid Properties (2P)

Fluid properties for two-phase fluid network

expand all in page
  • Two-Phase Fluid Properties (2P) block

Libraries:
Simscape / Foundation Library / Two-Phase Fluid / Utilities

Description

The Two-Phase Fluid Properties (2P) block sets the thermophysical properties of a fluid in a two-phase fluid network. These properties, which include density, viscosity, and specific heat, among others, can extend into the supercritical region of the fluid (water, by default, with a supercritical region extending up to 100 MPa in pressure).

The properties apply to the whole of the two-phase fluid network (the group of continuously connected two-phase fluid blocks). A network can have only one working fluid, and therefore only one instance of this block. If the network is modeled without this block, the fluid is set to water and its properties are obtained from the domain definition.

The block parameterizes the fluid properties in terms of pressure and normalized internal energy—a linear transformation of the specific internal energy. In a subcooled liquid, the normalized internal energy definition is

u¯=u−uminusatL(p)−umin−1,umin≤u<uLsat(p),

where:

  • u¯ is the normalized internal energy of the fluid.

  • u is the specific internal energy of the fluid.

  • umin is the lowest specific internal energy allowed in the two-phase fluid network.

  • uLsat is the specific internal energy of the liquid phase at saturation.

In a superheated vapor, the normalized internal energy definition is

u¯=u−umaxumax−usatV(p)+2,uVsat(p)<u≤umax,

where:

  • umax is the highest specific internal energy allowed in the two-phase fluid network.

  • uVsat is the specific internal energy of the vapor phase at saturation.

In a two-phase mixture, the normalized internal energy definition is

u¯=u−usatL(p)usatV(p)−usatL(p),uLsat(p)≤u≤uVsat(p).

These expressions correspond to a normalized internal energy that is at all pressures -1 at the minimum valid specific internal energy, 0 at the liquid saturation boundary, +1 at the vapor saturation boundary, and +2 at the maximum valid specific internal energy.

In a two-phase mixture, the normalized internal energy ranges in value from 0 to 1 and is therefore equivalent to vapor quality—the mass fraction of the vapor phase in a two-phase mixture. In subcooled liquid and superheated vapor, the normalized internal energy behaves as an extension of vapor quality.

The normalized internal energy provides an advantage over the specific internal energy. It transforms the p-u phase diagram so that the subcooled liquid and superheated vapor phases occupy distinct rectangular regions. This transformation, shown in the figure, enables you to specify the fluid properties on separate rectangular p-u¯ grids, one for each phase.

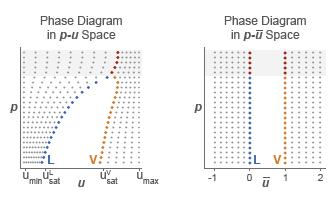
A pressure vector, of length N, and two normalized internal energy vectors, of lengths ML and MV, provide the (p, u¯) coordinates of the two grids. The pressure vector is common to both grids. The subcooled liquid grid is ML-by-N in size and the superheated vapor grid MV-by-N.

Two-way lookup tables provide the fluid property values on the (p, u¯) grids. The table rows correspond to different normalized internal energies and the table columns to pressures. Fluid properties in the p-u¯ continuum are computed using linear interpolation between the p-u¯ data points.

Two-Way Property Lookup Table

Saturated specific internal energy vectors provide the phase boundaries in the (p, u¯) phase diagram. These separate the different regions of the phase diagram—subcooled liquid, two-phase mixture, and superheated vapor.

Along with the minimum and maximum valid specific internal energy values, the saturated specific internal energy vectors enable the Two-Phase Fluid blocks to convert the normalized internal energies specified in this block into the specific internal energies they use for calculation purposes.

Supercritical Fluids

The fluid can become supercritical. Liquid and vapor then cease to exist as separate phases. Their saturation boundaries merge, forming what is known as the pseudocritical line (in the figure, the segment extending upward from the hump of the p–u phase diagram).

The pseudocritical line divides the fluid into liquid-like and vapor-like regions. As the phases are no longer distinct, however, the transition between the regions is gradual rather than abrupt. This means that at the pseudocritical line, the liquid-like and vapor-like fluids must share the same physical properties.

Property Tables

In this block, the liquid-like portion of the supercritical region is conceived as an extension of the liquid phase. Likewise, the vapor-like portion is conceived as an extension of the vapor phase. In other words, the properties of the supercritical fluid are divided into the liquid and vapor property tables of the block.

The distinction between the phases is, however, superfluous in the supercritical region. For breakpoints over the critical pressure, the liquid and vapor property tables must agree at the saturated boundaries (or, more properly, at the pseudocritical line). The supercritical portions of the tables then behave as a continuous whole.

Consider the kinematic viscosity tables as an example. The bottom row of the Liquid kinematic viscosity table parameter, as it corresponds to a normalized specific internal energy of 1, gives the data for the saturated liquid. The elements in that row corresponding to pressures at or above the critical point give the data over the pseudocritical line.

Likewise, the upper row of the Vapor kinematic viscosity table parameter, as it corresponds to a normalized specific internal energy of 1, gives the data for the saturated vapor. The elements in that row corresponding to pressures at or above the critical point therefore give the data over the pseudocritical line. To be valid, this data must be exactly the same as that given over the pseudocritical line in the liquid table.

Pseudocritical Line

The pseudocritical line is encoded in the saturation boundaries of the liquid and vapor phases. These are specified in the block via the Saturated liquid specific internal energy vector and Saturated vapor internal energy vector parameters. At pressures below the critical point, the values in one vector will generally differ from those in the other; above the critical point, however, one must always equal the other.

The pseudocritical line can assume any shape. For a simple approximation, it often suffices to extend the specific internal energy of the critical point upward along the pressure axis. This means setting the supercritical portions of the saturated specific internal energy vectors to that critical value. If the exact shape of the pseudocritical line is known, the specific internal energies along that line can be used instead.

Thermal Transport Properties

The data for the thermal transport properties—the specific heat, thermal conductivity, and Prandtl number—often shows a large peak near the critical point. The scale and size of the peak can, in some cases, cause numerical problems during simulation. To avoid such problems, the block allows the peak to be clipped. This option is specified in the Thermal transport properties near critical point block parameter (by setting it to Clip peak values).

The clipping is limited to a small pressure range around the critical point. That range is specified as a fraction of the critical pressure (f in the figure), and it extends in both directions (by the same amount) from the critical pressure. Within that range, the thermal properties are each limited to a maximum given by the greater of its two end values. The figure shows a plot of the Prandtl number for water with clipping.

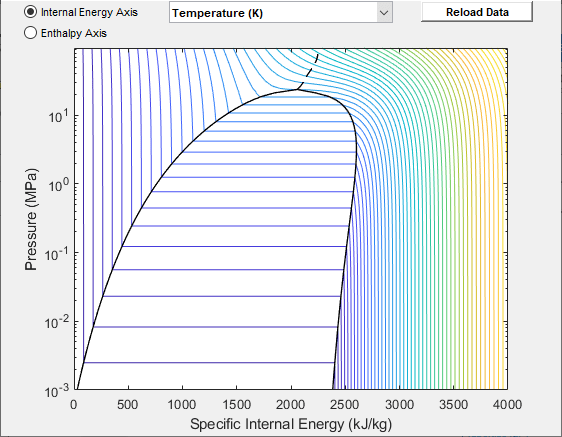
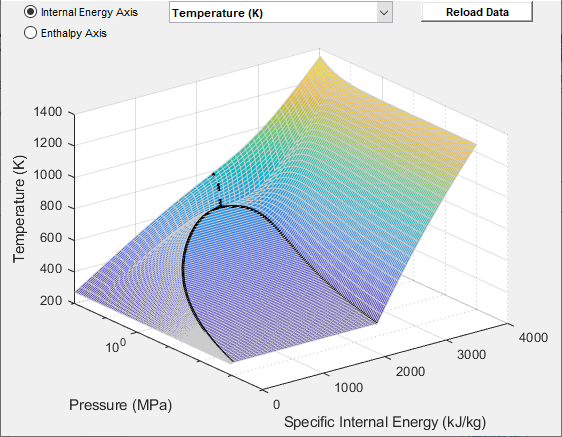
Data Visualization

The block lets you plot the specified two-phase fluid properties as a function of pressure and specific internal energy. Plotting the properties lets you visualize the data before simulating the model.

To plot the data, right-click a Two-Phase Fluid Properties (2P) block in your model and, from the context menu, select Foundation Library > Plot Fluid Properties (3D) or Foundation Library > Plot Fluid Properties (Contours). Use the drop-down list located at the top of the plot to select the property to visualize. Click the Reload button to regenerate a plot following a block parameter update.

Fluid Properties (3D) Plot

Fluid Properties (Contours) Plot

Examples

Cavitation in Two-Phase Fluid

Cavitation in Two-Phase Fluid

How two-phase fluid components can be used to simulate cavitation. The model is a translational mechanical converter driven by an oscillating pressure source. During the negative portion of the pressure source cycle, the fluid cavitates, reducing the force produced by the converter. As a result, the converter displacement drifts and does not return to the starting position.

Fluid Vaporization in Pipe

Fluid Vaporization in Pipe

Model the vaporization of water to generate steam. Liquid water enters the pipe at 370 K at a rate of 1 kg/s. The pipe is heated to 1000 K, causing the water flowing inside pipe to saturate.

Ports

Conserving

expand all

Conserving port that connects the block to the two-phase fluid network. You can connect it to any point on a two-phase fluid connection line in a block diagram. When you connect the Two-Phase Fluid Properties (2P) block to a connection line, the software automatically identifies the two-phase fluid blocks connected to the particular circuit and propagates the properties to all these blocks.

Parameters

expand all

Parameters

Lowest specific internal energy allowed in the two-phase fluid network.

Highest specific internal energy allowed in the two-phase fluid network.

Vector of length N containing the pressure values corresponding to the columns of the fluid property tables.

The default vector is a logarithmically spaced 100-element vector ranging from 1e-3 to 100 MPa, spanning both subcritical and supercritical regions of the fluid.

Pressure at which liquid and vapor cease to exist as distinct phases. Set this parameter to inf to model a fluid that is always subcritical.

Select whether to clip the peaks of the thermal transport properties near the critical point:

  • Clip peak values ― If the peaks are sharp and large, clip them to avoid numerical issues during simulation. Use the Fraction above and below Critical pressure for clipping parameter to specify the width of the clipping region.

  • Do not clip peak values ― Leave the thermal transport properties as is.

Pressure range above and below the critical pressure, expressed as a fraction, for clipping the peaks of the thermal transport properties.

Dependencies

To enable this parameter, set Thermal transport properties near critical point to Clip peak values.

Absolute pressure of the environment.

Select what happens if the moist air pressure or temperature go beyond the valid range during simulation:

  • None ― The block does not return an error if the properties go out of range.

  • Warning ― The block issues a warning, but continues the simulation.

  • Error ― The block returns an error and stops the simulation.

Dynamic pressure at which the flow at a port begins to reverse direction. The dynamic pressure is the difference between the total pressure and the static pressure. Treat this parameter as a means to smooth the flow reversal. Larger values correspond to smoother reversals and smaller values to sharper reversals.

The two-phase fluid domain uses an upwind scheme that derives the flow rate at a port from its value just upwind of the port. During flow reversals, the source of the flow rate value changes abruptly and the flow rate can become discontinuous. To prevent discontinuities and improve simulation robustness, flow reversals are smoothed out, with the dynamic pressure threshold marking the beginning of the smoothed transitions.

Liquid Properties

Vector of length ML containing the normalized internal energy values corresponding to the rows of the liquid property tables. The vector must begin at -1 and end at 0 (the saturated liquid state).

The default is a uniformly spaced 25-element vector.

ML × N matrix containing the liquid specific volume values corresponding to the normalized liquid internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Vapor specific volume table parameter.

The default matrix is a 25 × 100 table for water.

ML × N matrix containing the liquid specific entropy values corresponding to the normalized liquid internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Vapor specific entropy table parameter.

The default matrix is a 25 × 100 table for water.

ML × N matrix containing the liquid temperature values corresponding to the normalized liquid internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Vapor temperature table parameter.

The default matrix is a 25 × 100 table for water.

ML × N matrix containing the liquid kinematic viscosity values corresponding to the normalized liquid internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Vapor kinematic viscosity table parameter.

The default matrix is a 25 × 100 table for water.

ML × N matrix containing the liquid thermal conductivity values corresponding to the normalized liquid internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Vapor thermal conductivity table parameter.

The default matrix is a 25 × 100 table for water.

ML × N matrix containing the liquid Prandtl number values corresponding to the normalized liquid internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Vapor Prandtl number table parameter.

The default matrix is a 25 × 100 table for water.

Vector of length N containing the saturated liquid specific internal energy values corresponding to the pressure vector. Elements at or above the critical pressure must equal their counterparts in the Saturated vapor specific internal energy vector block parameter.

The default is a 100-element vector for water.

Vapor Properties

Vector of length MV containing the normalized internal energy values corresponding to the rows of the vapor property tables. The vector must begin at 1 (the saturated vapor state) and end at 2.

The default is a uniformly spaced 25-element vector.

MV × N matrix containing the vapor specific volume values corresponding to the normalized vapor internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Liquid specific volume table parameter.

The default matrix is a 25 × 100 table for water.

MV × N matrix containing the vapor specific entropy values corresponding to the normalized vapor internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Liquid specific entropy table parameter.

The default matrix is a 25 × 100 table for water.

MV × N matrix containing the vapor temperature values corresponding to the normalized vapor internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Liquid temperature table parameter.

The default matrix is a 25 × 100 table for water.

MV × N matrix containing the vapor kinematic viscosity values corresponding to the normalized vapor internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Liquid kinematic viscosity table parameter.

The default matrix is a 25 × 100 table for water.

MV × N matrix containing the vapor thermal conductivity values corresponding to the normalized vapor internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Liquid thermal conductivity table parameter.

The default matrix is a 25 × 100 table for water.

MV × N matrix containing the vapor Prandtl number values corresponding to the normalized vapor internal energy and pressure vectors. Elements at the saturation boundary and at or above the critical pressure must equal their counterparts in the Liquid Prandtl number table parameter.

The default matrix is a 25 × 100 table for water.

Vector of length N containing the saturated vapor specific internal energy values corresponding to the pressure vector. Elements at or above the critical pressure must equal their counterparts in the Saturated liquid specific internal energy vector block parameter.

The default is a 100-element vector for water.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2015b

expand all

See Also

Topics