Hard Stops in the Position-Based Translational Domain
This example shows how to configure Translational Hard Stop (PB) blocks in several simple position-based mechanical translational models and interpret the model behavior. This example describes how to model systems with upper and lower bounds, choose a hard stop model parameterization, set initial targets for variables, and interpret the logged forces.
Ball Bouncing on the Ground
Open the model ConfiguringHardStopsBallBouncingOnGround.
open_system('ConfiguringHardStopsBallBouncingOnGround');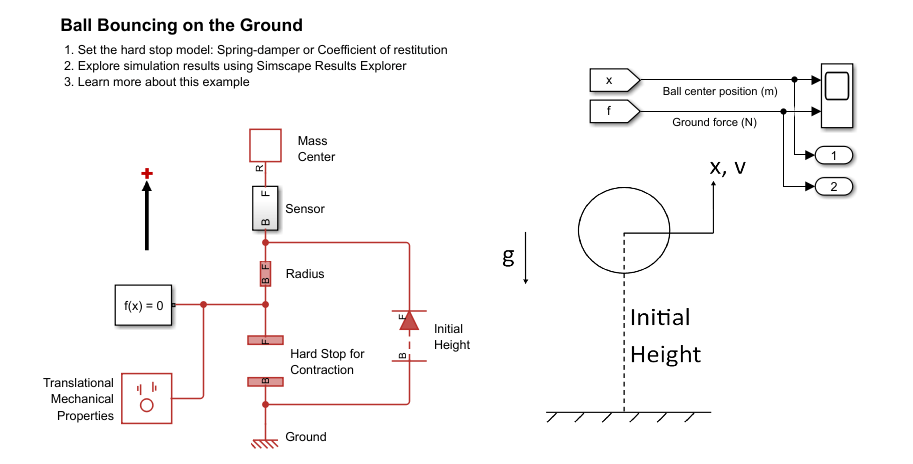
The model represents a ball that bounces on the ground, traveling in the vertical direction. Gravity acts downward, the ball has a mass of 0.5 kg and radius of 15 cm. In this scenario, the ball has an initial height of 8 m above the ground.
In the model, the entire ball mass is concentrated at a single point, labeled Mass Center. The Radius block provides a constant distance offset between the ball center and the ground. The Hard Stop block models the contact between the ball and ground. In the translational mechanical domain, gravity always acts downward. A translational mechanical properties block specifies the network positive direction incline angle as 90 deg. Therefore, gravity acts in the negative direction.
The Initial Height block sets the initial distance between the ball center and ground. The Initial Height block has a high priority target length of 8 m between the ball center and ground. The Radius block has a high priority length of 15 cm. The Mass Center block has a high priority target of 0 m/s for its initial velocity. These three high priority targets fully specify the model initial conditions, so all other variable targets have priorities of none.
Open the Sensor subsystem.
open_system('ConfiguringHardStopsBallBouncingOnGround/Sensor');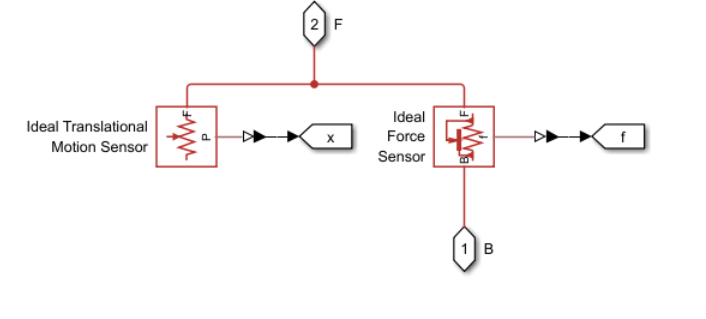
The Sensor subsystem senses the absolute position of the ball center and the force of the ground acting on the ball. The Ideal Force Sensor (PB) block senses force flowing from port B to port F, meaning it senses the force of the system at port B acting on the system at port F. The force sensor measures a positive force when port B exerts a positive force on port F, which is equivalent to a state of compression because port F has a more positive position than port B. The sensor measures a negative force when port B exerts a negative force on port F, which is equivalent to a state of tension. Keeping in line with the position-based mechanical translational force conventions, the sensor B and F ports align with the subsystem B and F ports and the network's global positive direction.
Simulate the model and open the scope.
open_system('ConfiguringHardStopsBallBouncingOnGround'); sim('ConfiguringHardStopsBallBouncingOnGround'); open_system('ConfiguringHardStopsBallBouncingOnGround/Scope');
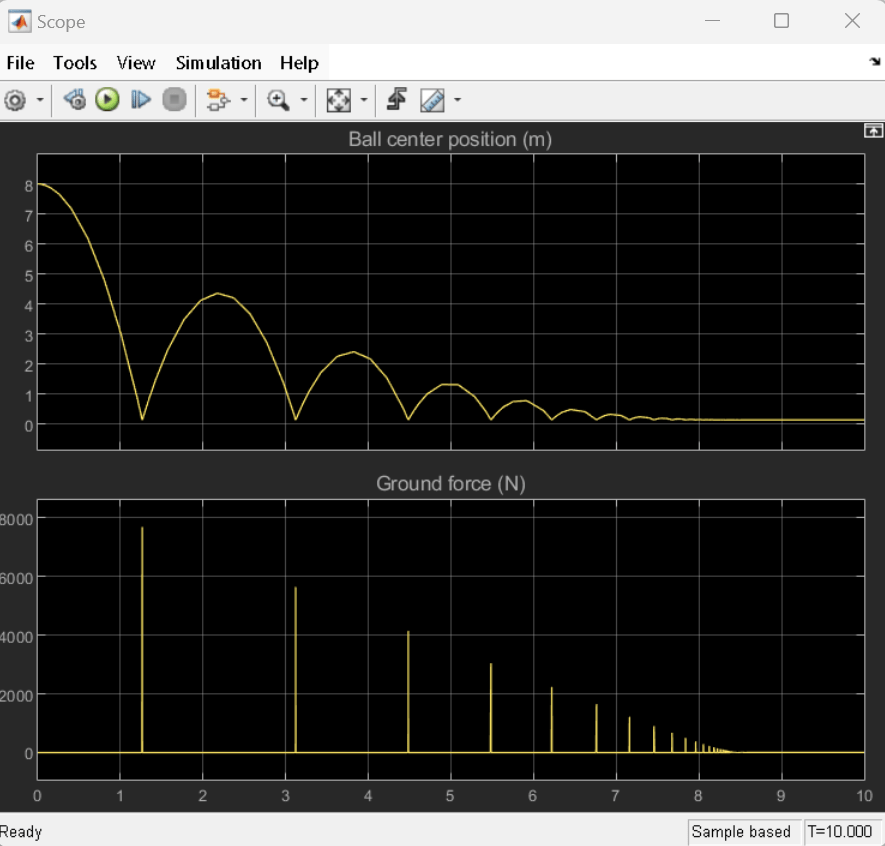
The ball starts at a position of 8 m and falls towards the ground. The ball bounces multiple times, losing energy on each collision. When the ball hits the ground, the ground imparts a large impulse on the ball in the upward direction.
Ball Bouncing Between Two Walls
Open the model ConfiguringHardStopsBallBouncingBetweenWalls.
open_system('ConfiguringHardStopsBallBouncingBetweenWalls');The model represents a ball that bounces between two walls, traveling in the horizontal direction. The ball has a mass of 0.5 kg and radius of 15 cm. The walls are spaced 10 m apart. The ball is initially in the middle of the gap between the walls and has a velocity of 10 m/s.
In the model, the entire ball mass is concentrated at a single point, labeled Mass Center. Spacer blocks named Left Radius and Right Radius model fixed radial distances on either side of the Mass Center. The Mass Center itself has the Length parameter set to 0 m. Setting the Length to zero allows the Ideal Translational Motion Sensor attached to the Mass Center B port to output the position of the mass center. Contact between the ball and two walls is modeled using two Hard stop (PB) blocks. The point where the ball leftmost point impacts the left wall is modeled using Left Hard Stop. Port B of Left Hard Stop is connected to the stationary World block, so it does not move and has a position of 0 m. The point where the ball rightmost point impacts the right wall is modeled using Right Hard Stop. Port F of the Right Hard Stop is stationary because it is connected a Spacer block that is connected to the stationary World block. The Spacer block sets the 10 m distance between the walls. A Translational Mechanical Properties block specifies the rail inclination as horizontal (0 degrees).
High priority initial targets set several constant distances and initial variable values in the model. The three Translational Spacer (PB) blocks, labeled Spacer, Left Radius, and Right Radius all have length as a high priority initial target, which specifies the distance between the two walls, the distance between the ball left edge and center, and the distance between the ball right edge and center, respectively. Lengths of the Translational Spacer (PB) blocks are constant throughout the simulation. The Initial Spacer block sets the initial distance between the ball center and right wall. The Initial Spacer block does not have an effect on the simulation after initialization. The Initial Spacer block has a high priority target length of 5 m. The Mass Center has a high priority target of 10 m/s for its initial velocity. These five high priority targets fully specify the model initial conditions, so all other variable targets have priorities of none.
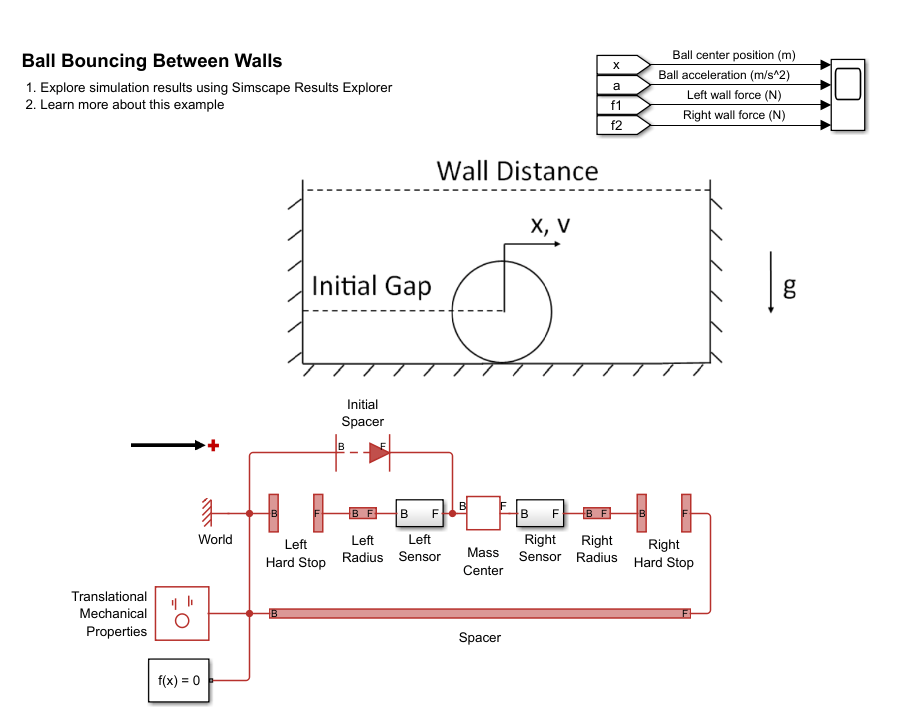
The Left Sensor subsystem contains a translational motion sensor for measuring the ball center position and acceleration and a force sensor for measuring impacts between the ball and left wall. The force sensor B and F ports are aligned with the network's positive direction. The Right Sensor subsystem contains a force sensor for measuring impacts between the ball and right wall.
open_system('ConfiguringHardStopsBallBouncingBetweenWalls/Left Sensor');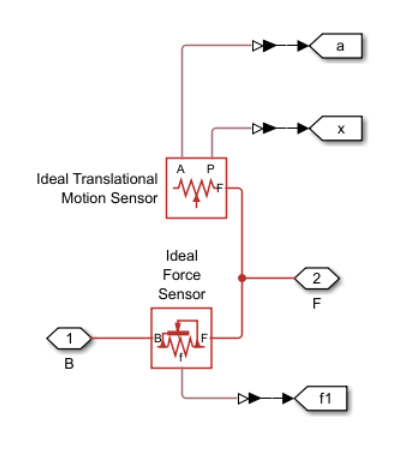
Simulate the model and open the scope.
open_system('ConfiguringHardStopsBallBouncingBetweenWalls'); sim('ConfiguringHardStopsBallBouncingBetweenWalls'); open_system('ConfiguringHardStopsBallBouncingBetweenWalls/Scope');
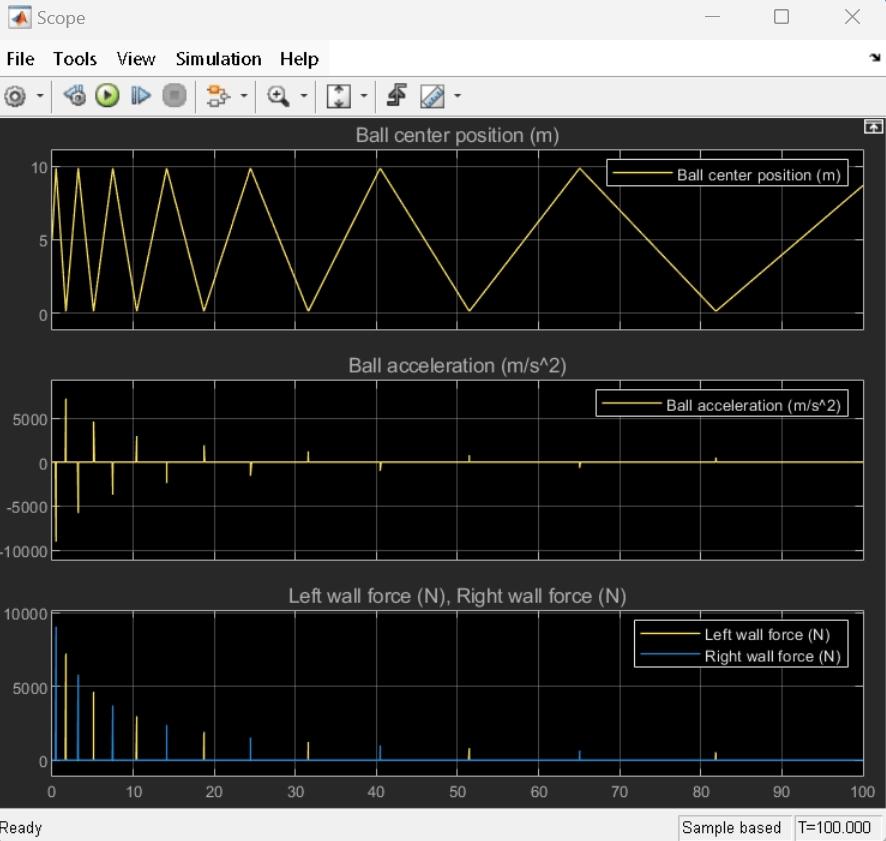
The ball starts at a position of 5 m and travels in the positive direction toward the right wall. When the ball hits the right wall, it experiences a large acceleration in the negative direction as it rapidly reverses direction. The ball then bounces between the walls, losing energy after each bounce. As the ball hits each wall, the corresponding force sensor measures a large positive force, corresponding to a hard stop in a state of compression. While the hard stop that is engaged undergoes a state of compression, the other hard stop is disengaged and registers zero force. The mass absorbs all of the hard stop force.
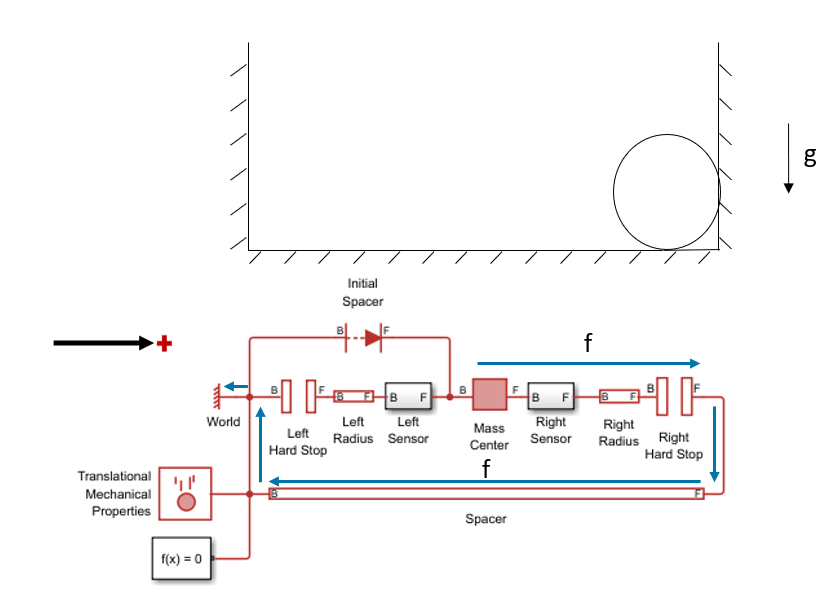
When the ball impacts the right wall, the Right Hard Stop imparts a large negative force on the ball to generate the large negative acceleration. The figure below depicts the physical view and force flow during the impact. Force flows out of Mass Center, corresponding to negative acceleration and negative logged force, f for the Mass Center block. Force flows from port B to port F in Right Sensor, Right Radius, and Right Hard Stop, corresponding to states of compression and positive logged force, f, in the two-port blocks. Force flows from port F to port B in Spacer, corresponding to a state of tension and negative logged force, f, in the Spacer block. Force flows into World, indicating that the World block provides a negative force on the Spacer block that prevents Spacer motion in the positive direction. Zero force flows through Left Hard Stop, Left Radius, and Left Sensor because the World and Mass Center blocks fully absorb the force.
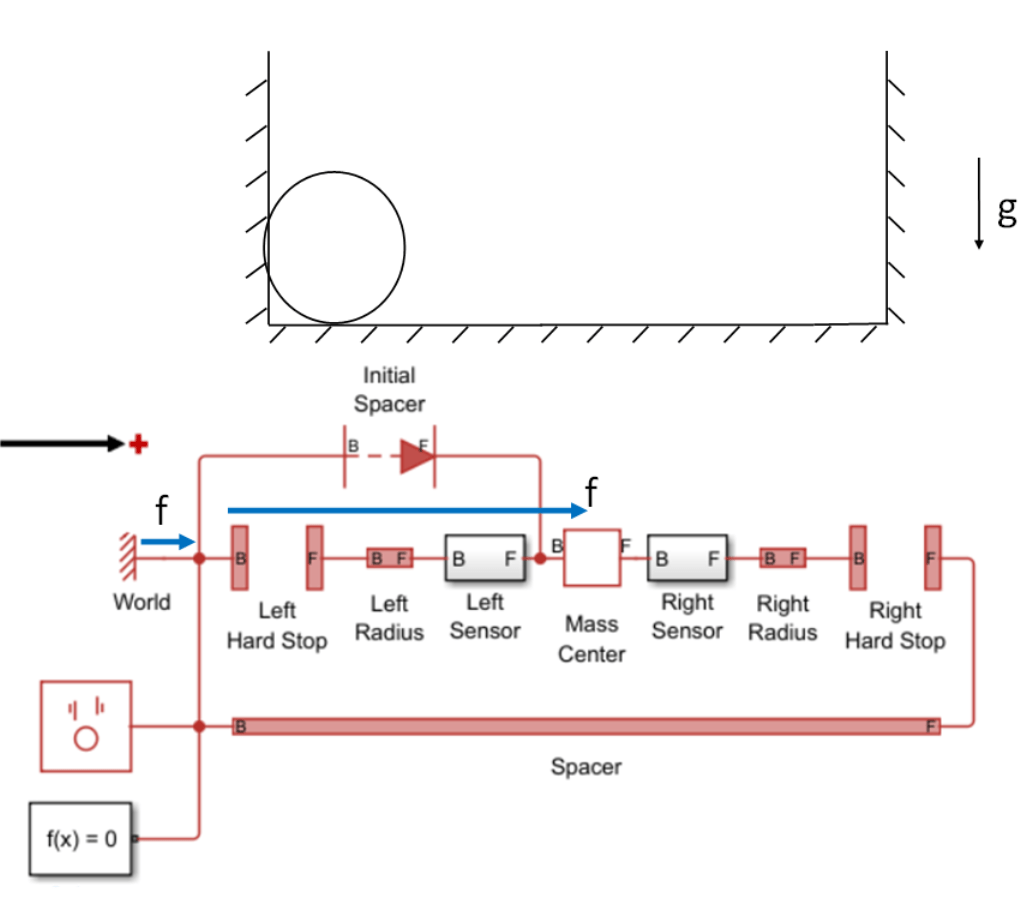
The figure below shows the physical view and schematic view force flow during a collision with the left wall. Force flows from port B to port F in the Left Hard Stop, Left Radius, and Left Sensor, corresponding to states of compression and positive logged force, f. Force flows into the Mass Center, corresponding to the mass accelerating in the positive direction. Force flows out of the World block, corresponding to the World block preventing the Left Hard Stop B port from moving in the negative direction. The rest of the position-based translational network has zero force flowing through it, corresponding to the World block and Mass Center block fully absorbing all of the force.
Light Cable Between Two Masses
Open the model ConfiguringHardStopsCableBetweenMasses.
open_system('ConfiguringHardStopsCableBetweenMasses');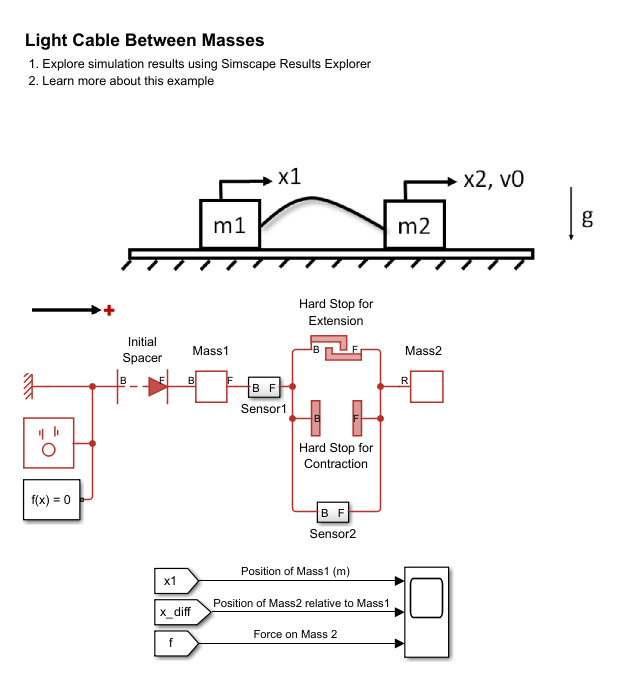
The model represents two masses that slide on a frictionless surface and are connected by a light cable. Initially, the masses are 0.5 m apart, the right mass has a velocity of 2 m/s, and the left mass is motionless. As the right mass slides to the right, the cable goes taut, snapping the left mass into motion and slowing down the right mass. The left mass then travels faster than the right mass and eventually collides into the right mass. When that collision occurs, the left mass loses speed and the right mass gains speed. Alternating cycles of the cable going taut and the masses colliding repeat as the masses continue to travel in the positive direction. The cable has a rest length of 1 m. The masses are modeled as point masses without any length.
Contact between the masses is modeled by the Hard Stop (PB) block labeled Mass Contact. The light cable is modeled by the Cable subsystem that is described below. An Initial Spacer block sets the initial position of Right Mass to 0 m. Mass Contact has a high priority Gap length of 0.5 m. Left Mass has a high priority target velocity of 0 m/s while Right Mass has a high priority target velocity of 2 m/s.
Open the Cable subsystem.
open_system('ConfiguringHardStopsCableBetweenMasses/Cable');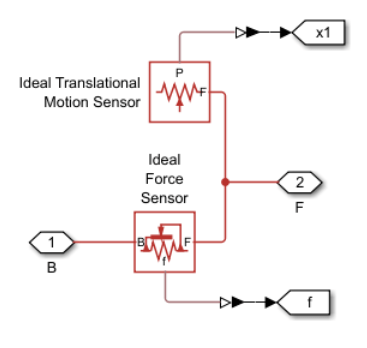
Connecting a Translational Hard Stop (PB) to a Translational Spacer (PB) models a hard stop for separation, or length upper-bound, between subsystem ports B and F. As subsystem ports B and F move apart, the hard stop ports move closer together. When the hard stop engages, the hard stop has a length of approximately 0 m, and the subsystem ports have a separation distance approximately equals the spacer length. The hard stop contact stiffness and damping represent the cable elongation stiffness and damping. The Translational Spacer (PB) specifies the cable length of 1 m using a high priority target for length.
Open the Sensor subsystem.
open_system('ConfiguringHardStopsCableBetweenMasses/Sensor1');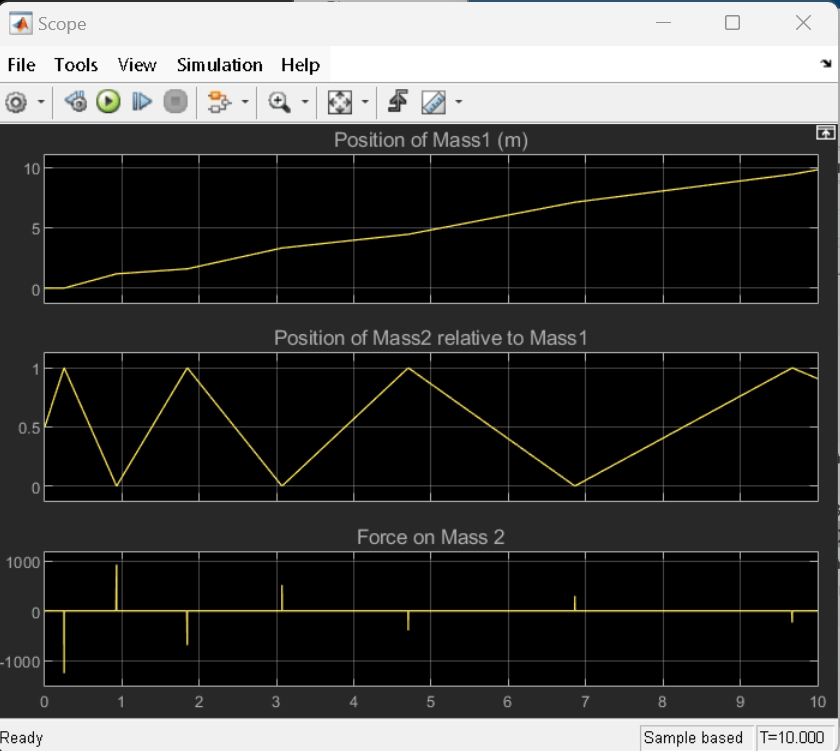
The Sensor1 subsystem senses the absolute position of Left Mass and the force flowing from Left Mass to the rest of the system. Force flowing from left Mass to the rest of the system is equivalent to the force flowing into Right Mass, due to this schematic topography.
Simulate the model and open the scope.
open_system('ConfiguringHardStopsCableBetweenMasses'); sim('ConfiguringHardStopsCableBetweenMasses'); open_system('ConfiguringHardStopsCableBetweenMasses/Scope');
When the simulation starts, Left Mass is at rest with a position of 0 m. Right Mass has a position of +0.5 m relative to Left Mass and a positive velocity. When Right Mass has a position of 1 m relative to Left Mass, the taut cable generates an impulse force between the masses. During the impulse, the force flowing from Left Mass to Right Mass has a negative sign, indicating that the system in between the two masses is in a state of tension. In a state of tension, the cable exerts a positive force on Left Mass and a negative force on Right Mass, accelerating Left Mass in the positive direction and Right mass in the negative direction.
At a simulation time of approximately 1 second, the masses collide. The force sensor measures a positive impulse force, indicating that the system in between the two masses is in a state of compression. In a state of compression, the Mass Contact hard stop exerts a negative force on Left Mass and a positive force on Right Mass.
Preloaded Spring
Open the model ConfiguringHardStopsPreloadedSpring.
open_system('ConfiguringHardStopsPreloadedSpring');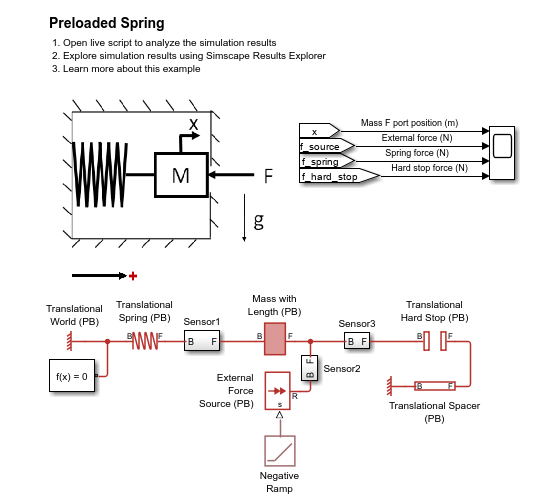
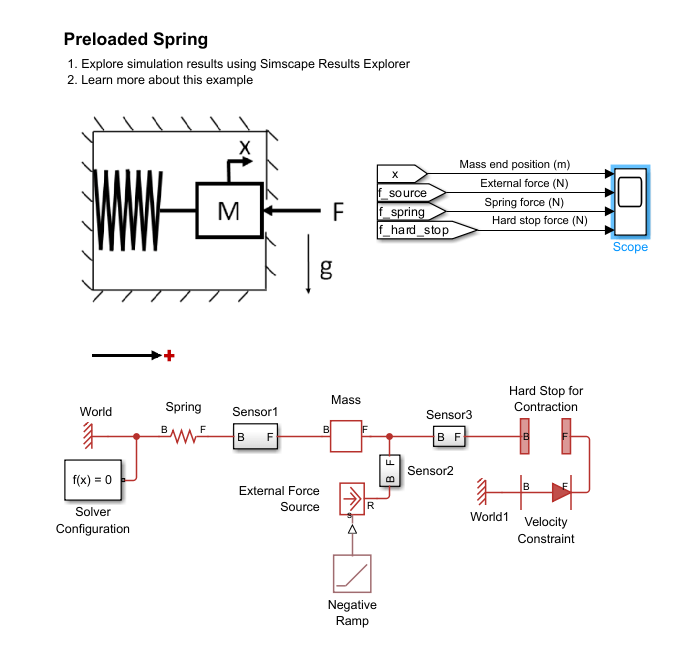
The model represents a mass on a preloaded spring under compression. The spring preload is generated by an outer casing. Initially the system is at rest. After 10 seconds, an external force pushes on the mass in the negative direction. Once the external force overcomes the preload, the mass begins to move in the negative direction.
The model represents the system using a Translational Spring (PB) in between a Translational World (PB) and Mass with Length (PB) block. The Translational Hard Stop (PB) block represents the outer casing that counteracts the spring preload. The F port of the hard stop is constrained to have a velocity of 0 m/s due to its connection to the Translational Spacer (PB) block that is connected to a World block. The Translational Spacer (PB) block length variable has an initialization priority of none. Therefore, the solver determines the position of the hard stop F port rather than requiring the user to specify it. In this model, you specify the following high priority targets:
Translational Spring (PB) Force of 100 N.
Translational Spring (PB) Length of 0.1 m.
Translational Hard Stop (PB) Force of 100 N.
Positive forces in the spring and hard stop correspond states of compression. 100 N is the chosen preload. When the external force is initially 0 N and the compressive spring and hard stop forces balance each other, the mass begins at rest. The initial spring length of 0.1 m is the spring length under the preload force.
Simulate the model and open the scope.
open_system('ConfiguringHardStopsPreloadedSpring'); sim('ConfiguringHardStopsPreloadedSpring'); open_system('ConfiguringHardStopsPreloadedSpring/Scope');
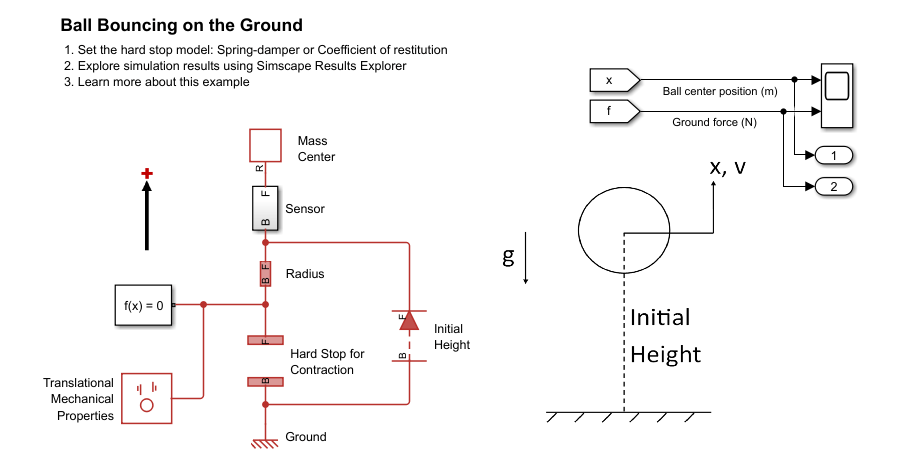
When the simulation starts, the external force is 0 N. The mass is motionless while the spring and hard stop balance each other, both with forces of 100 N in states of compression. At 10 seconds, the external force source begins to push on the mass in the negative direction. The hard stop force begins to decrease while the spring force remains at the preload value and the mass remains motionless. When the external force exceeds the preload at 20 seconds, the hard stop is disengaged, the spring force begins to increase, and the mass moves in the negative direction.
Comparing Hard Stop Parameterizations
The hard stop block contains several parameterization options. Three hard stop models are based on stiffness and damping while one hard stop model is based on a coefficient of restitution.
The model based on a coefficient of restitution is represented by a mode chart with two regular modes and two instantaneous modes:
FREE— There is no force transmission between the sides of the hard stop (M = 0).CONTACT— The gap is closed (M = 1).RELEASE— The instantaneous mode needed to transition fromCONTACTtoFREE(M = 2).IMPACT— The instantaneous mode used when the sides bounce together (M = 3).
M is a logged flag indicating the mode. Unlike the models based on stiffness and damping, the coefficient of restitution model does not allow penetration of the two sides of the hard stop.
When the hard stop gap length approaches 0 slowly, with speeds less than the static contact speed threshold, the two sides of the hard stop stay in contact. Otherwise, the sides bounce. When the sides bounce, they lose relative speed due to the coefficient of restitution. In the contact mode, the relative speed of the sides is v = 0. To transition from the contact mode to the free mode, the hard stop must be put into a state of tension greater than the Static contact release force threshold.
The coefficient of restitution modeling option improves simulation performance because the static contact mode does not require the block to keep computing hard stop force when the block is in contact mode.
Since high-velocity impacts are instantaneous for the coefficient of restitution model, variable step solvers do not log the impulse forces.
Open the BouncingBall model and close the scope.
open_system('ConfiguringHardStopsBallBouncingOnGround'); close_system('ConfiguringHardStopsBallBouncingOnGround/Scope');
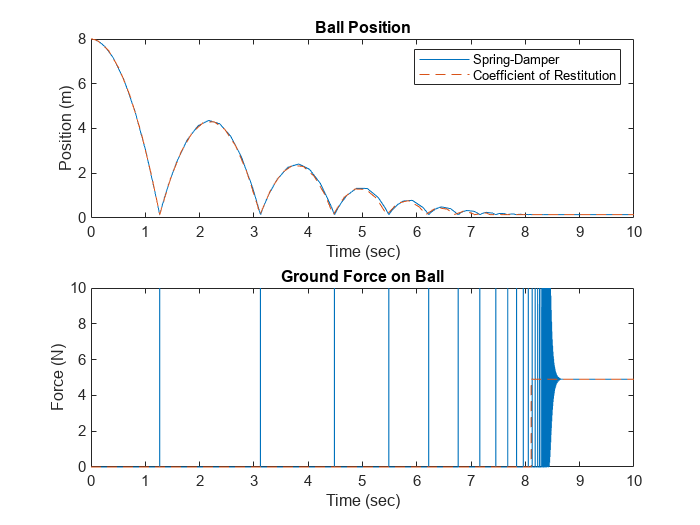
Simulate the model using a spring-damper hard stop parameterization.
set_param('ConfiguringHardStopsBallBouncingOnGround/Hard Stop',... 'model', 'simscape.enum.hardstop.smooth'); sim('ConfiguringHardStopsBallBouncingOnGround'); t_springDamper = tout; x_springDamper = yout(:,1); f_springDamper = yout(:,2);
Simulate the model using the coefficient of restitution parameterization.
set_param('ConfiguringHardStopsBallBouncingOnGround/Hard Stop',... 'model', 'simscape.enum.hardstop.modechart'); sim('ConfiguringHardStopsBallBouncingOnGround'); t_restitutionCoefficient = tout; x_restitutionCoefficient = yout(:,1); f_restitutionCoefficient = yout(:,2);
Plot the simulation behavior for the two hard stop models.
figure; subplot(2,1,1); plot(t_springDamper, x_springDamper) hold on plot(t_restitutionCoefficient, x_restitutionCoefficient, '--'); legend('Spring-Damper', 'Coefficient of Restitution') title('Ball Position') xlabel('Time (sec)'); ylabel('Position (m)'); subplot(2,1,2); plot(t_springDamper, f_springDamper) hold on plot(t_restitutionCoefficient, f_restitutionCoefficient, '--'); ylim([0 10]) title('Ground Force on Ball') xlabel('Time (sec)'); ylabel('Force (N)');
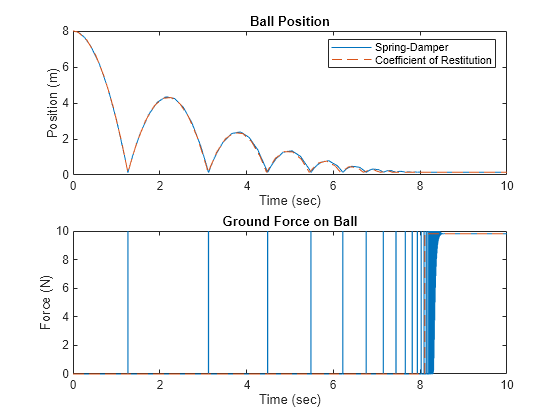
After some tuning, the two hard stop models can produce nearly identical position responses. The force responses appear different because the coefficient of restitution model does not log instantaneous impulse forces for a variable step solver. While the ball is in the air, both hard stop models exert a force of 0 N on the ball. Once the ball has come to rest, both hard stop models measure the ground's upward reaction force that counters the weight of the ball. In this scenario, the coefficient of restitution model requires much fewer time steps and has lower computational cost than the spring damper model:
num_steps_springDamper = numel(t_springDamper)
num_steps_springDamper = 2793
num_steps_restitutionCoefficient = numel(t_restitutionCoefficient)
num_steps_restitutionCoefficient = 117