FEM-Parameterized Induction Machine (Wound Rotor)

Wound-rotor induction machine defined in terms of magnetic flux linkage

Since R2023b

Libraries:
Simscape / Electrical / Electromechanical / Asynchronous

Description

The FEM-Parameterized Induction Machine (Wound Rotor) block models a wound-rotor induction machine using magnetic flux linkage tables.

You can generate the magnetic flux linkage tables with a finite element tool such as ANSYS Motor-CAD software.

A wound-rotor asynchronous machine is a type of induction machine. You can access all the stator and rotor connections on the block. Therefore, you can model soft-start regimes using a switch between wye and delta configurations or by increasing rotor resistance. If you do not need access to the rotor windings, you can use the FEM-Parameterized Induction Machine (Squirrel Cage) block instead.

Connect port ~1 to a three-phase circuit. To connect the stator in delta configuration, connect a Phase Permute block between ports ~1 and ~2. To connect the stator in wye configuration, connect port ~2 to a Grounded Neutral (Three-Phase) or Floating Neutral (Three-Phase) block.

If you do not need to vary the rotor resistance, connect the rotor port ~1r' to a Floating Neutral (Three-Phase) block and rotor port ~2r' to a Grounded Neutral (Three-Phase) block.

The rotor circuit is referred to the stator. Therefore, when you use the block in a circuit, refer any additional circuit parameters to the stator.

Equations

A three-phase wound-rotor induction machine consists of an iron stator lamination with three copper windings and a rotor lamination with three copper windings.

When a three-phase AC supply feeds the stator, the current produces a rotating magnetic field. This rotating field induces currents in the rotor windings, which produce a magnetic field in the rotor. The interaction between these magnetic fields and the currents produces a torque in the rotor, which starts its motion.

The induction machine equations are expressed in a synchronous reference frame orientated with the rotor field (SRFORF). This frame is synchronous with the stator and rotor magnetic fields, and the D-axis is aligned with the rotor field D-axis. The rotor magnetic flux linkage vector only has a D-axis component in this frame. The Q-axis component is zero.

${λ^{'}}_{q r} = 0.$

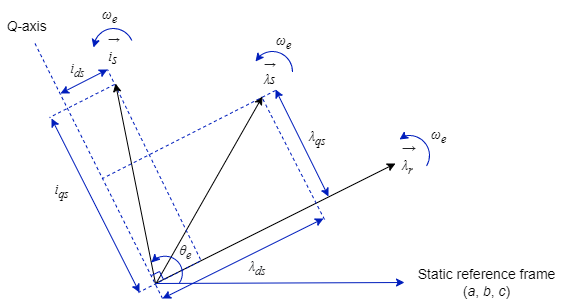
$\vec{λ_{s}}$ is the stator magnetic field vector.
$\vec{λ_{r}}$ is the rotor magnetic field vector.
$\vec{i_{s}}$ is the stator current vector.

All of these vectors rotate at the synchronous speed ω_e. The synchronous angle θ_e tracks the orientation of the stator current vector.

The rotor current vector rotates at a speed given by this equation:

$ω_{s l i p} = ω_{e} - N_{p p} ω_{r},$

where ω_r is the rotor mechanical speed and N_pp is the Number of pole pairs parameter.

To express the stator a-, b-, and c-phase voltages and currents in the SRFORF reference frame, you can use the Park transform:

$P_{s} = 2 / 3 [\begin{matrix} \cos θ_{e} & \cos (θ_{e} - 2 π / 3) & \cos (θ_{e} + 2 π / 3) \\ - \sin θ_{e} & - \sin (θ_{e} - 2 π / 3) & - \sin (θ_{e} + 2 π / 3) \\ 0.5 & 0.5 & 0.5 \end{matrix}],$

where θ_e is the time integral of the synchronous speed:

$θ_{e} = \int ω_{e} d t .$

You can then compute the D-axis and Q-axis components of stator voltages and currents using these equations.

$\begin{array}{l} i s_{d q 0} = P_{s} \cdot i s_{a b c} \\ v s_{d q 0} = P_{s} \cdot v s_{a b c} \end{array}$

The rotor a-, b-, and c-phase voltages and currents do not rotate at the synchronous speed due to slip. Rotor currents rotate at the slip speed ω_slip.

To express rotor DQ currents in the stationary frame (a, b, and c phases) you can use the Park transform:

$P_{r} = 2 / 3 [\begin{matrix} \cos θ_{e r} & \cos (θ_{e r} - 2 π / 3) & \cos (θ_{e r} + 2 π / 3) \\ - \sin θ_{e r} & - \sin (θ_{e r} - 2 π / 3) & - \sin (θ_{e r} + 2 π / 3) \\ 0.5 & 0.5 & 0.5 \end{matrix}],$

where θ_er is the rotor slip angle, equal to the time integral of the slip speed:

$θ_{e r} = \int ω_{s l i p} d t .$

Then, you can compute the a, b, and c components of rotor voltages and currents using these equations.

$\begin{array}{l} i r_{a b c} = P_{r}^{- 1} \cdot i r_{d q 0} \\ v r_{a b c} = P_{r}^{- 1} \cdot v r_{d q 0} \end{array}$

In the SRFORF reference frame, the stator and rotor currents, voltages, and fluxes are related to these fundamental induction machine equations:

Stator voltage equations

$\begin{array}{l} v_{d s} = R_{s} i_{d s} - ω_{e} λ_{q s} + \frac{d λ_{d s}}{d t} \\ v_{q s} = R_{s} i_{q s} + ω_{e} λ_{d s} + \frac{d λ_{q s}}{d t} \end{array}$
Rotor voltage equations

$\begin{array}{l} {v^{'}}_{d r} = {R^{'}}_{r} {i^{'}}_{d r} + \frac{d {λ^{'}}_{d r}}{d t} \\ {v^{'}}_{q r} = {R^{'}}_{r} {i^{'}}_{q r} + ω_{s l i p} {λ^{'}}_{d r} \end{array}$

Use the latter rotor voltage equation to compute the slip speed, which you can then use to compute the synchronous speed for the reference frame transformations.

$ω_{s l i p} = \frac{{v^{'}}_{q r} - {R^{'}}_{r} {i^{'}}_{q r}}{{λ^{'}}_{d r}} .$
Wound rotor equations

$\begin{array}{l} {v^{'}}_{d r} = V r_{d} \\ {v^{'}}_{q r} = V r_{q} \end{array}$
where Vr_d and Vr_q are the D-axis and Q-axis rotor voltages across ports ~1r' and ~2r', respectively.
Flux-current relationships
The magnetizing D-axis current is defined as

$i_{d} = i_{d s} + {i^{'}}_{d r},$

and the flux-current relationships are

$\begin{array}{l} {λ^{'}}_{d r} = λ_{d s} - L_{t} i_{d s} \\ {λ^{'}}_{q r} = λ_{q s} - L_{t} i_{q s} \end{array}$

where:
- λ_ds is the interpolated value of the Stator d-axis flux linkage table, λds(ids,iqs) parameter computed for the particular combination of i_d and i_qs.
- λ_qs is the interpolated value of the Stator q-axis flux linkage table, λqs(ids,iqs) parameter computed for the particular combination of i_d and i_qs.
- L_t is the interpolated value of the transient inductance computed from the magnetic flux linkage tables.
An alternative form of the rotor flux-current relationships uses the L_ϕ inductance

$\begin{array}{l} {λ^{'}}_{d r} = L_{ϕ} i_{d} \\ {λ^{'}}_{q r} = L_{ϕ} i_{q} \end{array}$

where L_ϕ is the interpolated value of the magnetizing inductance table computed from the flux linkage tables.
When you combine the latter equation for the Q-axis rotor flux with ${λ^{'}}_{q r} = 0$ you obtain $i_{q} = 0$ , which means that the referred rotor Q-axis current is equal and opposite to the stator Q-axis current:

${i^{'}}_{q r} = - i_{q s} .$

L_ϕ is defined by this equation.

$L_{ϕ} = L_{s} - L_{t},$

where L_t is the transient inductance is defined as

$L_{t} = L_{s} - \frac{L_{m}^{2}}{{L^{'}}_{r}} .$

In these equations L_s, L_m, and ${L^{'}}_{r}$ are the stator inductance, the magnetizing inductance, and the referred rotor inductance respectively. These equations relate these inductances:

$\begin{array}{l} L_{s} = L_{l s} + L_{m} \\ {L^{'}}_{r} = {L^{'}}_{l r} + L_{m} \end{array}$

where L_ls and ${L^{'}}_{l r}$ are the stator leakage inductance and the referred rotor leakage inductance, respectively.
Torque equation

$T = \frac{3}{2} N_{p p} (λ_{d s} i_{q s} - λ_{q s} i_{d s}) .$

Model Thermal Effects

You can expose thermal ports to simulate the effects of generated heat and motor temperature. To expose the thermal ports and enable the Temperature Dependence and Thermal Port parameters, set the Modeling option parameter to one of these options:

No thermal port — The block contains electrical conserving ports associated with the stator windings, but does not contain thermal ports.
Show thermal port — The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.

For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.

Variables

To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.

Examples

Model Start-Up Control Strategy for Wound-Rotor Induction Motor

Design a start-up control strategy with a resistor for a wound-rotor induction model using a Simscape™ Electrical™ FEM-Parameterized Induction Machine (Wound Rotor) block.

Since R2023b
Open Live Script

Ports

Conserving

expand all

~1 — Stator positive-end connections
electrical

Composite three-phase port associated with the stator positive-end connections. For more information about three-phase ports, see Three-Phase Ports.

~2 — Stator negative-end connections
electrical

Composite three-phase port associated with the stator negative-end connections.

R — Machine rotor
mechanical rotational

Mechanical rotational conserving port associated with the machine rotor.

C — Machine case
mechanical rotational

Mechanical rotational conserving port associated with the machine case.

~1r' — Rotor positive-end connections
electrical

Composite three-phase port associated with the rotor positive-end connections. For more information about three-phase ports, see Three-Phase Ports.

~2r' — Rotor negative-end connections
electrical

Composite three-phase port associated with the rotor negative-end connections. For more information about three-phase ports, see Three-Phase Ports.

HA — a-phase terminal
thermal

Thermal conserving port associated with the a-phase terminal.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HB — b-phase terminal
thermal

Thermal conserving port associated with the b-phase terminal.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HC — c-phase terminal
thermal

Thermal conserving port associated with the c-phase terminal.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HR — Rotor
thermal

Thermal conserving port associated with the rotor.

Dependencies

To enable this port, set Modeling option to Show thermal port.

Parameters

expand all

Modeling option — Option to enable thermal ports
`No thermal port` (default) | `Show thermal port`

Option to enable the thermal ports of the block and model the effects of generated heat and machine temperature.

Resistance

Stator resistance, Rs — Stator resistance
`0.25` `Ohm` (default) | positive scalar

Stator resistance.

Tabulate rotor resistance with frequency — Option to tabulate rotor resistance with frequency
`Off` (default) | `On`

Option to tabulate the rotor resistance with the frequency.

Clear this parameter to specify a constant rotor resistance at the rated temperature.

Select this parameter to specify resistance as a function of frequency at the rated temperature.

Referred rotor resistance, Rr_d — Referred rotor resistance
`0.14` `Ohm` (default) | positive scalar

Rotor resistance referred to the stator.

Dependencies

To enable this parameter, clear the Tabulate rotor resistance with frequency parameter.

Rotor AC frequency vector, fr — Rotor AC frequency vector
`[0, 5, 10, 15]` `Hz` (default) | vector of nonnegative scalars

Rotor AC frequency vector.

Dependencies

To enable this parameter, select the Tabulate rotor resistance with frequency parameter.

Referred rotor resistance table, Rr_d(fr) — Referred rotor resistance table
`[.14, .14, .14, .14]` `Ohm` (default) | vector of positive scalars

Table of rotor resistance referred to the stator as a function of the rotor AC frequency vector.

Dependencies

To enable this parameter, select the Tabulate rotor resistance with frequency parameter.

Flux

Number of pole pairs — Machine pole pairs
`1` (default) | positive integer

Number of machine pole pairs.

Stator d-axis current vector, iDS — Stator D-axis current vector
`[0, 150, 350, 500]` `A` (default) | vector of nonnegative scalars

Stator D-axis current vector.

Stator q-axis current vector, iQS — Stator Q-axis current vector
`[0, 250, 500]` `A` (default) | vector of nonnegative scalars

Stator Q-axis current vector.

Stator d-axis flux linkage table, λds(ids,iqs) — Stator D-axis flux linkage table
`4.4e-2 * repmat([0, 150, 350, 500]', 1, 3)` `Wb` (default) | matrix of scalars

Stator D-axis flux linkage table.

The default value corresponds to linear flux. Using linear flux is equivalent to the modeling approach of the Induction Machine Squirrel Cage block.

Stator q-axis flux linkage table, λqs(ids,iqs) — Stator Q-axis flux linkage table
`2.1e-3 * repmat([0, 250, 500], 4, 1)` `Wb` (default) | matrix of scalars

Stator Q-axis flux linkage table.

The default value corresponds to linear flux. Using linear flux is equivalent to the modeling approach of the Induction Machine Squirrel Cage block.

Interpolation method — Interpolation method
`Linear` (default) | `Smooth`

Interpolation method for approximating the output value when the input value is between grid points:

Linear — Use an extension of the linear algorithm for multidimensional interpolation. Select this option to get the best performance.
Smooth — Use a modified Akima interpolation algorithm. Select this option to produce a continuous surface with continuous first-order derivatives.

For more information about interpolation methods, see tablelookup.

Mechanical

Include rotor inertia — Option to include rotor inertia
`On` (default) | `Off`

Option to include rotor inertia.

Rotor inertia — Rotor inertia
`1e-3` `kg*m^2` (default) | positive scalar

Rotor inertia.

Dependencies

To enable this parameter, select the Include rotor inertia parameter.

Rotor damping — Rotor damping
`0` `Nms/rad` (default) | nonnegative scalar

Rotor damping.

Temperature Dependence

To enable these parameters, set Modeling option to Show thermal port.

Measurement temperature — Rated temperature
`298.15` `K` (default) | real scalar

Temperature at which you quote the motor parameters.

Stator resistance temperature coefficient — Stator resistance temperature coefficient
`3.93e-3` `1/K` (default) | nonnegative scalar

Coefficient α in the equation relating resistance to temperature for all three stator windings. For more information, see Thermal Model for Actuator Blocks. The default value is for copper.

Rotor resistance temperature coefficient — Rotor resistance temperature coefficient
`3.93e-3` `1/K` (default) | nonnegative scalar

Coefficient α in the equation relating resistance to temperature for the rotor. For more information, see Thermal Model for Actuator Blocks. The default value is for copper.

Thermal Port

To enable these parameters, set Modeling option to Show thermal port.

Include stator and rotor thermal masses — Option to include stator and rotor thermal masses
`On` (default) | `Off`

Option to include stator and rotor thermal masses.

Thermal mass for each stator winding — Winding thermal mass
`100` `J/K` (default) | positive scalar

Thermal mass value for each stator winding. The thermal mass is the energy required to raise the temperature by one degree.

Dependencies

To enable this parameter, select the Include stator and rotor thermal masses parameter.

Rotor thermal mass — Rotor thermal mass
`200` `J/K` (default) | positive scalar

Thermal mass of the rotor. The thermal mass is the energy required to raise the temperature of the rotor by one degree.

Dependencies

To enable this parameter, select the Include stator and rotor thermal masses parameter.

References

[1] Carbonieri, Matteo, Nicola Bianchi, and Luigi Alberti. “Induction Motor Mapping Using Rotor Field-Oriented Analysis Technique.” In 2019 IEEE Energy Conversion Congress and Exposition (ECCE), 2321–28. Baltimore, MD, USA: IEEE, 2019. https://doi.org/10.1109/ECCE.2019.8912787.

[2] Carbonieri, Matteo, Lino Di Leonardo, Marco Tursini, Marco Villani, and Mircea Popescu. “Induction Motor Performance Prediction Using Static FEA: Method Description and Comparison With Time-Domain Approach.” In 2020 IEEE Energy Conversion Congress and Exposition (ECCE), 1351–56. Detroit, MI, USA: IEEE, 2020. https://doi.org/10.1109/ECCE44975.2020.9236246.

[3] Troncon, Diego, Matteo Carbonieri, Luigi Alberti, and Nicola Bianchi. “Measures and Simulations of Induction Machines Flux Linkage Characteristics Based on Rotor Field Orientation.” IEEE Transactions on Industry Applications 57, no. 5 (September 2021): 4686–93. https://doi.org/10.1109/TIA.2021.3089662.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2023b

FEM-Parameterized Induction Machine (Wound Rotor)

Description

Equations

Model Thermal Effects

Variables

Examples

Model Start-Up Control Strategy for Wound-Rotor Induction Motor

Ports

Conserving

~1 — Stator positive-end connections electrical

~2 — Stator negative-end connections electrical

R — Machine rotor mechanical rotational

C — Machine case mechanical rotational

~1r' — Rotor positive-end connections electrical

~2r' — Rotor negative-end connections electrical

HA — a-phase terminal thermal

Dependencies

HB — b-phase terminal thermal

Dependencies

HC — c-phase terminal thermal

Dependencies

HR — Rotor thermal

Dependencies

Parameters

Modeling option — Option to enable thermal ports No thermal port (default) | Show thermal port

Resistance

Stator resistance, Rs — Stator resistance 0.25 Ohm (default) | positive scalar

Tabulate rotor resistance with frequency — Option to tabulate rotor resistance with frequency Off (default) | On

Referred rotor resistance, Rr_d — Referred rotor resistance 0.14 Ohm (default) | positive scalar

Dependencies

Rotor AC frequency vector, fr — Rotor AC frequency vector [0, 5, 10, 15] Hz (default) | vector of nonnegative scalars

Dependencies

Referred rotor resistance table, Rr_d(fr) — Referred rotor resistance table [.14, .14, .14, .14] Ohm (default) | vector of positive scalars

Dependencies

Flux

Number of pole pairs — Machine pole pairs 1 (default) | positive integer

Stator d-axis current vector, iDS — Stator D-axis current vector [0, 150, 350, 500] A (default) | vector of nonnegative scalars

Stator q-axis current vector, iQS — Stator Q-axis current vector [0, 250, 500] A (default) | vector of nonnegative scalars

Stator d-axis flux linkage table, λds(ids,iqs) — Stator D-axis flux linkage table 4.4e-2 * repmat([0, 150, 350, 500]', 1, 3) Wb (default) | matrix of scalars

Stator q-axis flux linkage table, λqs(ids,iqs) — Stator Q-axis flux linkage table 2.1e-3 * repmat([0, 250, 500], 4, 1) Wb (default) | matrix of scalars

Interpolation method — Interpolation method Linear (default) | Smooth

Mechanical

Include rotor inertia — Option to include rotor inertia On (default) | Off

Rotor inertia — Rotor inertia 1e-3 kg*m^2 (default) | positive scalar

Dependencies

Rotor damping — Rotor damping 0 N*m*s/rad (default) | nonnegative scalar

Temperature Dependence

Measurement temperature — Rated temperature 298.15 K (default) | real scalar

Stator resistance temperature coefficient — Stator resistance temperature coefficient 3.93e-3 1/K (default) | nonnegative scalar

Rotor resistance temperature coefficient — Rotor resistance temperature coefficient 3.93e-3 1/K (default) | nonnegative scalar

Thermal Port

Include stator and rotor thermal masses — Option to include stator and rotor thermal masses On (default) | Off

Thermal mass for each stator winding — Winding thermal mass 100 J/K (default) | positive scalar

Dependencies

Rotor thermal mass — Rotor thermal mass 200 J/K (default) | positive scalar

Dependencies

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Topics

~1 — Stator positive-end connections
electrical

~2 — Stator negative-end connections
electrical

R — Machine rotor
mechanical rotational

C — Machine case
mechanical rotational

~1r' — Rotor positive-end connections
electrical

~2r' — Rotor negative-end connections
electrical

HA — a-phase terminal
thermal

HB — b-phase terminal
thermal

HC — c-phase terminal
thermal

HR — Rotor
thermal

Modeling option — Option to enable thermal ports
`No thermal port` (default) | `Show thermal port`

Stator resistance, Rs — Stator resistance
`0.25` `Ohm` (default) | positive scalar

Tabulate rotor resistance with frequency — Option to tabulate rotor resistance with frequency
`Off` (default) | `On`

Referred rotor resistance, Rr_d — Referred rotor resistance
`0.14` `Ohm` (default) | positive scalar

Rotor AC frequency vector, fr — Rotor AC frequency vector
`[0, 5, 10, 15]` `Hz` (default) | vector of nonnegative scalars

Referred rotor resistance table, Rr_d(fr) — Referred rotor resistance table
`[.14, .14, .14, .14]` `Ohm` (default) | vector of positive scalars

Number of pole pairs — Machine pole pairs
`1` (default) | positive integer

Stator d-axis current vector, iDS — Stator D-axis current vector
`[0, 150, 350, 500]` `A` (default) | vector of nonnegative scalars

Stator q-axis current vector, iQS — Stator Q-axis current vector
`[0, 250, 500]` `A` (default) | vector of nonnegative scalars

Stator d-axis flux linkage table, λds(ids,iqs) — Stator D-axis flux linkage table
`4.4e-2 * repmat([0, 150, 350, 500]', 1, 3)` `Wb` (default) | matrix of scalars

Stator q-axis flux linkage table, λqs(ids,iqs) — Stator Q-axis flux linkage table
`2.1e-3 * repmat([0, 250, 500], 4, 1)` `Wb` (default) | matrix of scalars

Interpolation method — Interpolation method
`Linear` (default) | `Smooth`

Include rotor inertia — Option to include rotor inertia
`On` (default) | `Off`

Rotor inertia — Rotor inertia
`1e-3` `kg*m^2` (default) | positive scalar

Rotor damping — Rotor damping
`0` `Nms/rad` (default) | nonnegative scalar

Measurement temperature — Rated temperature
`298.15` `K` (default) | real scalar

Stator resistance temperature coefficient — Stator resistance temperature coefficient
`3.93e-3` `1/K` (default) | nonnegative scalar

Rotor resistance temperature coefficient — Rotor resistance temperature coefficient
`3.93e-3` `1/K` (default) | nonnegative scalar

Include stator and rotor thermal masses — Option to include stator and rotor thermal masses
`On` (default) | `Off`

Thermal mass for each stator winding — Winding thermal mass
`100` `J/K` (default) | positive scalar

Rotor thermal mass — Rotor thermal mass
`200` `J/K` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.