Characterize Condenser Microphone Model

Since R2024b

This example shows how to characterize a condenser microphone model using the Variable Gap Capacitor block.

The condenser microphone, also known as a capacitive microphone, functions via changes in capacitance between the moveable and fixed plates of the variable gap capacitor. Acoustic sound pressure causes the thin diaphragm, which represents the moveable plate, to vibrate. This vibration changes the distance between the plates, which changes the capacitance. The Variable Gap Capacitor block presents an interface between the plates of the capacitor, which act as a mechanical translational system, and the capacitor which acts as an electrical component. You apply a bias voltage across the movable and the fixed bottom electrodes so the electronic circuitry detects the change in capacitance.

Model Overview

Open the CondenserMicrophone model.

model = "CondenserMicrophone";
open_system(model);

The Variable Gap Capacitor block named Diaphragm Capacitance connects the diaphragm structural model with the electrical circuit that measures the output voltage.

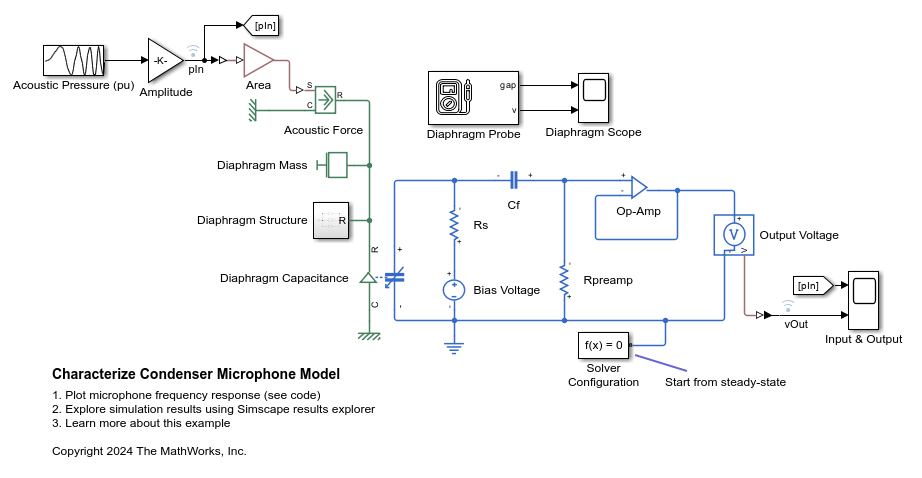
Set the parameters you need to model the diaphragm and electrical circuit, based on geometry and material properties.

diameter = 14e-3; % Diameter of the circular diaphragm [m]
area = pi*(diameter/2)^2; % Effective radiating area of the diaphragm [m^2]
airgap = 25e-6; % Nominal air gap [m]
epsr = 1.0006; % Relative permittivity of air
membraneStiffness = 7500; % Stiffness of the membrane [N/m]
membraneThickness = 1e-6; % Thickness of the membrane (for mass calculation) [m]
membraneDensity = 8300; % Mass density of membrane material [kg] 
mass = membraneDensity*membraneThickness*area; % Effective membrane mass [kg]
biasVoltage = 12; % DC voltage you apply to the diaphragm [V]

Run Simulations to Obtain Microphone Frequency Response

To characterize the microphone, apply an acoustic pressure of constant amplitude and linearly increasing frequency. To study the microphone behavior at different sound levels, run multiple simulations with different acoustic pressure amplitudes.

acousticPressureValues = [1e-2, 1e-1, 1, 10]; % [Pa]
minFreq = 20; % Hz
maxFreq = 20000; % Hz

Set up and run the simulations.

simIn = createSimInput(model, acousticPressureValues, minFreq, maxFreq);
runInParallel = false;
if runInParallel
    simOut = parsim(simIn,ShowProgress="on");
else
    simOut = sim(simIn,ShowProgress="on",UseFastRestart="on");
end

[21-Aug-2024 20:18:55] Running simulations...
[21-Aug-2024 20:19:14] Completed 1 of 4 simulation runs
[21-Aug-2024 20:19:24] Completed 2 of 4 simulation runs
[21-Aug-2024 20:19:34] Completed 3 of 4 simulation runs
[21-Aug-2024 20:19:45] Completed 4 of 4 simulation runs

Plot Microphone Frequency Response

Represent the frequency response of the transfer function between the input sound pressure signal and the output microphone voltage.

CondenserMicrophonePlotFrequencyResponse

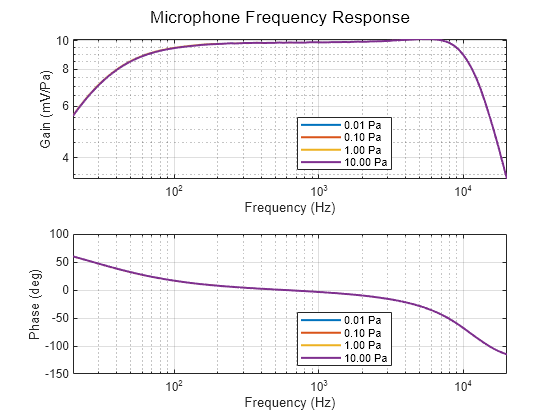
Observe that the frequency response is nearly identical for all the acoustic pressure levels, which indicates that this microphone maintains the same sensibility and linear behavior at a wide range of sound amplitudes.

Supporting Function

function simIn = createSimInput(modelName, acousticAmplitudeValues, minFreq, maxFreq)
% Creates the Simulink.SimulationInput object array, where each of the
% simulations has a different acousticPressure set to the corresponding
% value in the acousticAmplitudeValues array
    nSims = length(acousticAmplitudeValues);
    simIn = Simulink.SimulationInput.empty(0,nSims);
    for iSim = 1:nSims
        simIn(iSim) = Simulink.SimulationInput(modelName);
        simIn(iSim) = simIn(iSim).setVariable("acousticPressure", acousticAmplitudeValues(iSim));
        simIn(iSim) = simIn(iSim).setVariable("minFreq", minFreq);
        simIn(iSim) = simIn(iSim).setVariable("maxFreq", maxFreq);
    end
end

References

[1] Thompson, Stephen. "Simscape Model of a Condenser Microphone." Accessed February 16, 2024. https://www.mathworks.com/matlabcentral/fileexchange/159738-simscape-model-of-a-condenser-microphone.