逻辑回归模型的贝叶斯分析
此示例说明如何使用 slicesample 对逻辑回归模型进行贝叶斯推断。
统计推断通常基于最大似然估计 (MLE)。MLE 选择能够使数据似然最大化的参数,是一种较为自然的方法。在 MLE 中,假定参数是未知但固定的数值,并在一定的置信度下进行计算。在贝叶斯统计中,使用概率来量化未知参数的不确定性,因而未知参数被视为随机变量。
贝叶斯推断
贝叶斯推断是结合有关模型或模型参数的先验知识来分析统计模型的过程。这种推断的根基是贝叶斯定理:
例如,假设我们有正态观测值
其中 sigma 是已知的,theta 的先验分布为
在此公式中,mu 和 tau(有时也称为超参数)也是已知的。如果您观测正态分布观测值 X 的 n 个样本,可以获得 theta 的正态共轭后验分布,如下所示:
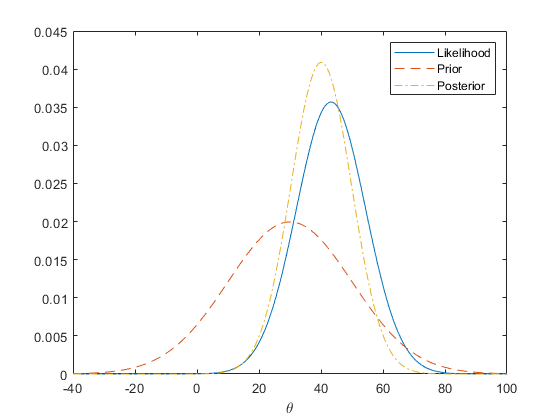
下图显示 theta 的先验、似然和后验。
rng(0,'twister'); n = 20; sigma = 50; x = normrnd(10,sigma,n,1); mu = 30; tau = 20; theta = linspace(-40, 100, 500); y1 = normpdf(mean(x),theta,sigma/sqrt(n)); y2 = normpdf(theta,mu,tau); postMean = tau^2*mean(x)/(tau^2+sigma^2/n) + sigma^2*mu/n/(tau^2+sigma^2/n); postSD = sqrt(tau^2*sigma^2/n/(tau^2+sigma^2/n)); y3 = normpdf(theta, postMean,postSD); plot(theta,y1,'-', theta,y2,'--', theta,y3,'-.') legend('Likelihood','Prior','Posterior') xlabel('\theta')
汽车试验数据
在一些简单的问题中,例如前面的正态均值推断示例,很容易计算出封闭形式的后验分布。但是,在涉及非共轭先验的一般问题中,后验分布很难或不可能通过分析来进行计算。我们将以逻辑回归作为示例。此示例包含一个试验,以帮助建模不同重量的汽车在里程测试中的未通过比例。数据包括被测汽车的重量、汽车数量以及失败次数等观测值。我们采用一组经过变换的重量,以减少回归参数估值的相关性。
% A set of car weights weight = [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]'; weight = (weight-2800)/1000; % recenter and rescale % The number of cars tested at each weight total = [48 42 31 34 31 21 23 23 21 16 17 21]'; % The number of cars that have poor mpg performances at each weight poor = [1 2 0 3 8 8 14 17 19 15 17 21]';
逻辑回归模型
逻辑回归(广义线性模型的一种特例)适合这些数据,因为响应变量呈二项分布。逻辑回归模型可以写作:
其中 X 是设计矩阵,b 是包含模型参数的向量。在 MATLAB® 中,我们可以将此方程写作:
logitp = @(b,x) exp(b(1)+b(2).*x)./(1+exp(b(1)+b(2).*x));
如果您有一些先验知识或者已经具备某些非信息性先验,则可以指定模型参数的先验概率分布。例如,在此示例中,我们使用正态先验值表示截距 b1 和斜率 b2,即
prior1 = @(b1) normpdf(b1,0,20); % prior for intercept prior2 = @(b2) normpdf(b2,0,20); % prior for slope
根据贝叶斯定理,模型参数的联合后验分布与似然和先验的乘积成正比。
post = @(b) prod(binopdf(poor,total,logitp(b,weight))) ... % likelihood * prior1(b(1)) * prior2(b(2)); % priors
请注意,此模型中后验的归一化常数很难进行分析。但是,即使不知道归一化常数,如果您知道模型参数的大致范围,也可以可视化后验分布。
b1 = linspace(-2.5, -1, 50); b2 = linspace(3, 5.5, 50); simpost = zeros(50,50); for i = 1:length(b1) for j = 1:length(b2) simpost(i,j) = post([b1(i), b2(j)]); end; end; mesh(b2,b1,simpost) xlabel('Slope') ylabel('Intercept') zlabel('Posterior density') view(-110,30)

此后验沿参数空间的对角线伸长,表明(在我们观察数据后)我们认为参数是相关的。这很有意思,因为在我们收集任何数据之前,我们假设它们是独立的。相关性来自我们的先验分布与似然函数的组合。
切片抽样
蒙特卡罗方法常用于在贝叶斯数据分析中汇总后验分布。其想法是,即使您不能通过分析的方式计算后验分布,也可以从分布中生成随机样本,并使用这些随机值来估计后验分布或推断的统计量,如后验均值、中位数、标准差等。切片抽样是一种算法,用于从具有任意密度函数的分布中进行抽样,已知项最多只有一个比例常数 - 而这正是从归一化常数未知的复杂后验分布中抽样所需要的。此算法不生成独立样本,而是生成马尔可夫序列,其平稳分布就是目标分布。因此,切片抽样器是一种马尔可夫链蒙特卡罗 (MCMC) 算法。但是,它与其他众所周知的 MCMC 算法不同,因为只需要指定缩放的后验,不需要建议分布或边缘分布。
此示例说明如何使用切片抽样器作为里程测试逻辑回归模型的贝叶斯分析的一部分,包括从模型参数的后验分布生成随机样本、分析抽样器的输出,以及对模型参数进行推断。第一步是生成随机样本。
initial = [1 1]; nsamples = 1000; trace = slicesample(initial,nsamples,'pdf',post,'width',[20 2]);
抽样器输出分析
从切片抽样器获取随机样本后,很重要的一点是研究诸如收敛和混合之类的问题,以确定将样本视为是来自目标后验分布的一组随机实现是否合理。观察边缘轨迹图是检查输出的最简单方法。
subplot(2,1,1) plot(trace(:,1)) ylabel('Intercept'); subplot(2,1,2) plot(trace(:,2)) ylabel('Slope'); xlabel('Sample Number');

从这些图中可以明显看出,在处理过程趋于平稳之前,参数起始值的影响会维持一段时间(大约 50 个样本)才会消失。
检查收敛以使用移动窗计算统计量(例如样本的均值、中位数或标准差)也很有帮助。这样可以产生比原始样本轨迹更平滑的图,并且更容易识别和理解任何非平稳性。
movavg = filter( (1/50)*ones(50,1), 1, trace); subplot(2,1,1) plot(movavg(:,1)) xlabel('Number of samples') ylabel('Means of the intercept'); subplot(2,1,2) plot(movavg(:,2)) xlabel('Number of samples') ylabel('Means of the slope');
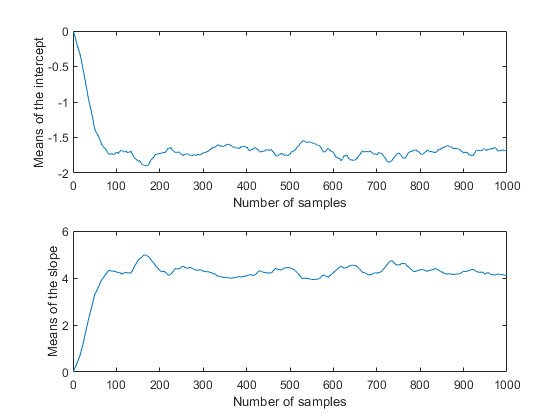
由于这些是基于包含 50 次迭代的窗口计算的移动平均值,因此前 50 个值无法与图中的其他值进行比较。然而,每个图的其他值似乎证实参数后验均值在 100 次左右迭代后收敛至平稳分布。同样显而易见的是,这两个参数彼此相关,与之前的后验密度图一致。
由于磨合期代表目标分布中不能合理视为随机实现的样本,因此不建议使用切片抽样器一开始输出的前 50 个左右的值。您可以简单地删除这些输出行,但也可以指定一个“预热”期。在已知合适的预热长度(可能来自先前的运行)时,这种方式很简便。
trace = slicesample(initial,nsamples,'pdf',post, ... 'width',[20 2],'burnin',50); subplot(2,1,1) plot(trace(:,1)) ylabel('Intercept'); subplot(2,1,2) plot(trace(:,2)) ylabel('Slope');

这些跟踪图没有显示出任何不平稳,表明预热期已完成。
但是,还需要了解跟踪图的另一方面。虽然截距的轨迹看起来像高频噪声,但斜率的轨迹好像具有低频分量,表明相邻迭代的值之间存在自相关。虽然也可以从这个自相关样本计算均值,但我们通常会通过删除样本中的冗余数据这一简便的操作来降低存储要求。如果它同时消除了自相关,我们还可以将这些数据视为独立值样本。例如,您可以通过只保留第 10 个、第 20 个、第 30 个等值来稀释样本。
trace = slicesample(initial,nsamples,'pdf',post,'width',[20 2], ... 'burnin',50,'thin',10);
要检查这种稀释的效果,可以根据轨迹估计样本自相关函数,并使用它们来检查样本是否快速混合。
F = fft(detrend(trace,'constant')); F = F .* conj(F); ACF = ifft(F); ACF = ACF(1:21,:); % Retain lags up to 20. ACF = real([ACF(1:21,1) ./ ACF(1,1) ... ACF(1:21,2) ./ ACF(1,2)]); % Normalize. bounds = sqrt(1/nsamples) * [2 ; -2]; % 95% CI for iid normal labs = {'Sample ACF for intercept','Sample ACF for slope' }; for i = 1:2 subplot(2,1,i) lineHandles = stem(0:20, ACF(:,i) , 'filled' , 'r-o'); lineHandles.MarkerSize = 4; grid('on') xlabel('Lag') ylabel(labs{i}) hold on plot([0.5 0.5 ; 20 20] , [bounds([1 1]) bounds([2 2])] , '-b'); plot([0 20] , [0 0] , '-k'); hold off a = axis; axis([a(1:3) 1]); end

第一个滞后的自相关值对于截距参数很明显,对于斜率参数更是如此。我们可以使用更大的稀释参数重复抽样,以进一步降低相关性。但为了完成本示例的目的,我们将继续使用当前样本。
推断模型参数
与预期相符,样本直方图模拟了后验密度图。
subplot(1,1,1) histogram2(trace(:,1),trace(:,2)); xlabel('Intercept') ylabel('Slope') zlabel('Posterior density') view(-110,30)
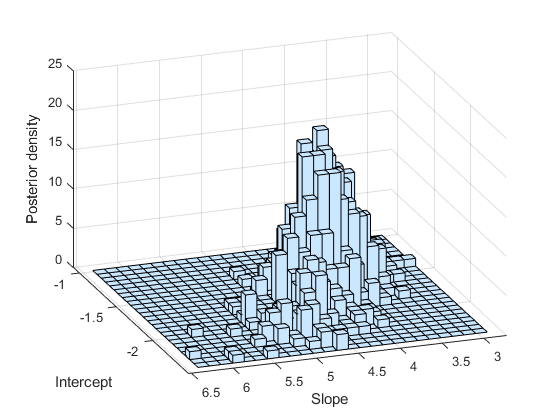
您可以使用直方图或核平滑密度估计值来总结后验样本的边缘分布属性。
subplot(2,1,1) histogram(trace(:,1)) xlabel('Intercept'); subplot(2,1,2) ksdensity(trace(:,2)) xlabel('Slope');

您还可以计算描述性统计量,例如随机样本的后验均值或百分位数。为了确定样本大小是否足以实现所需的精度,将所需的轨迹统计量作为样本数的函数来进行监视会很有帮助。
csum = cumsum(trace); subplot(2,1,1) plot(csum(:,1)'./(1:nsamples)) xlabel('Number of samples') ylabel('Means of the intercept'); subplot(2,1,2) plot(csum(:,2)'./(1:nsamples)) xlabel('Number of samples') ylabel('Means of the slope');
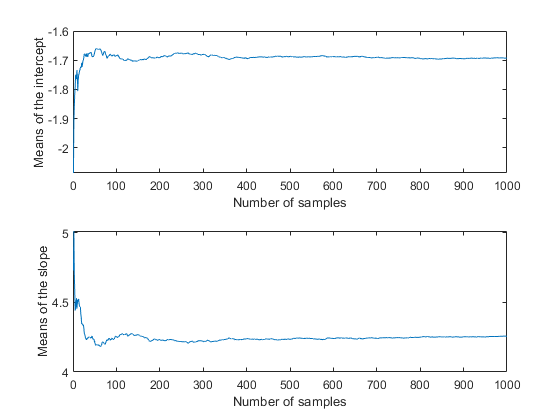
在这种情况下,样本大小 1000 似乎足以为后验均值估计值提供良好的精度。
bHat = mean(trace)
bHat = 1×2
-1.6931 4.2569
总结
Statistics and Machine Learning Toolbox™ 提供了多种函数,让您能够轻松地指定似然和先验。您也可以将它们结合起来用于推断后验分布。使用 slicesample 函数,您可以通过马尔可夫链蒙特卡罗模拟在 MATLAB 中执行贝叶斯分析。甚至在使用标准随机数生成器难以抽样的后验分布问题中也可以使用此函数。