bernstein
Bernstein polynomials
Description
bernstein(
with a function handle f,n,t)f returns the
nth-order Bernstein polynomial
symsum(nchoosek(n,k)*t^k*(1-t)^(n-k)*f(k/n),k,0,n), evaluated at
the point t. This polynomial approximates the function
f over the interval [0,1].
bernstein(
with a symbolic expression or function g,n,t)g returns the
nth-order Bernstein polynomial, evaluated at the point
t. This syntax regards g as a
univariate function of the variable determined by
symvar(g,1).
If any argument is symbolic, bernstein converts all arguments
except a function handle to symbolic, and converts a function handle’s results to
symbolic.
Examples
Approximation of Sine Function Specified as Function Handle
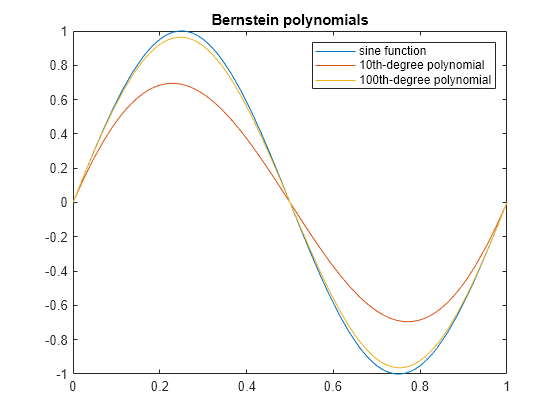
Approximate the sine function by the 10th- and 100th-degree Bernstein polynomials.
syms t
b10 = bernstein(@(t) sin(2*pi*t), 10, t);
b100 = bernstein(@(t) sin(2*pi*t), 100, t);Plot sin(2*pi*t) and its approximations.
fplot(sin(2*pi*t),[0,1]) hold on fplot(b10,[0,1]) fplot(b100,[0,1]) legend('sine function','10th-degree polynomial',... '100th-degree polynomial') title('Bernstein polynomials') hold off
Approximation of Exponential Function Specified as Symbolic Expression
Approximate the exponential function by the second-order
Bernstein polynomial in the variable t:
syms x t bernstein(exp(x), 2, t)
ans = (t - 1)^2 + t^2*exp(1) - 2*t*exp(1/2)*(t - 1)
Approximate the multivariate exponential function. When you approximate a
multivariate function, bernstein regards it as a univariate
function of the default variable determined by symvar. The
default variable for the expression y*exp(x*y) is
x:
syms x y t symvar(y*exp(x*y), 1)
ans = x
bernstein treats this expression as a univariate function of
x:
bernstein(y*exp(x*y), 2, t)
ans = y*(t - 1)^2 + t^2*y*exp(y) - 2*t*y*exp(y/2)*(t - 1)
To treat y*exp(x*y) as a function of the variable
y, specify the variable explicitly:
bernstein(y*exp(x*y), y, 2, t)
ans = t^2*exp(x) - t*exp(x/2)*(t - 1)
Approximation of Linear Ramp Specified as Symbolic Function
Approximate function f representing a
linear ramp by the fifth-order Bernstein polynomials in the variable
t:
syms f(t) f(t) = triangularPulse(1/4, 3/4, Inf, t); p = bernstein(f, 5, t)
p = 7*t^3*(t - 1)^2 - 3*t^2*(t - 1)^3 - 5*t^4*(t - 1) + t^5
Simplify the result:
simplify(p)
ans = -t^2*(2*t - 3)
Numerical Stability of Simplified Bernstein Polynomials
When you simplify a high-order symbolic Bernstein polynomial, the result often cannot be evaluated in a numerically stable way.
Approximate this rectangular pulse function by the 100th-degree Bernstein polynomial, and then simplify the result.
f = @(x)rectangularPulse(1/4,3/4,x);
b1 = bernstein(f, 100, sym('t'));
b2 = simplify(b1);Convert the polynomial b1 and the simplified polynomial b2 to MATLAB® functions.
f1 = matlabFunction(b1); f2 = matlabFunction(b2);
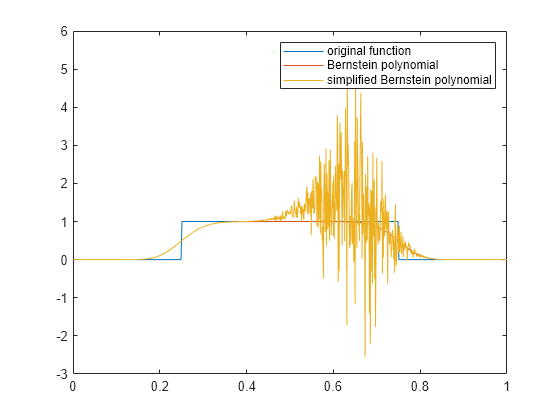
Compare the plot of the original rectangular pulse function, its numerically stable Bernstein representation f1, and its simplified version f2. The simplified version is not numerically stable.
t = 0:0.001:1; plot(t, f(t), t, f1(t), t, f2(t)) hold on legend('original function','Bernstein polynomial',... 'simplified Bernstein polynomial') hold off
Input Arguments
More About
Tips
Symbolic polynomials returned for symbolic
tare numerically stable when substituting numerical values between0and1fort.If you simplify a symbolic Bernstein polynomial, the result can be unstable when substituting numerical values for the curve parameter
t.
Version History
Introduced in R2013b
See Also
bernsteinMatrix | formula | nchoosek | symvar | symsum