Differentiation

Open Live Script

This example shows how to analytically find and evaluate derivatives using Symbolic Math Toolbox™. In the example you will find the 1st and 2nd derivative of f(x) and use these derivatives to find local maxima, minima and inflection points.

First Derivatives: Finding Local Minima and Maxima

Computing the first derivative of an expression helps you find local minima and maxima of that expression. Before creating a symbolic expression, declare symbolic variables:

syms x

By default, solutions that include imaginary components are included in the results. Here, consider only real values of x by setting the assumption that x is real:

assume(x, 'real')

As an example, create a rational expression (i.e., a fraction where the numerator and denominator are polynomial expressions).

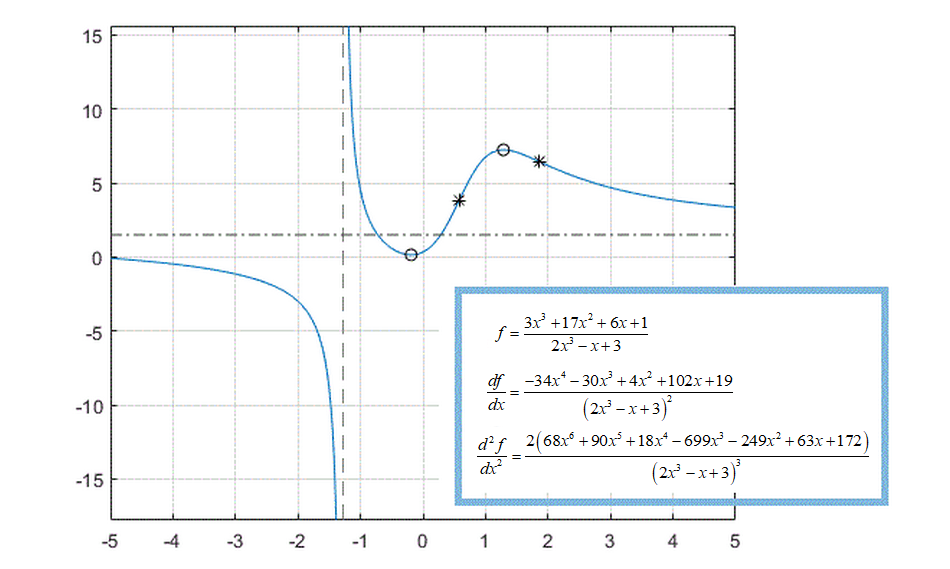
f = (3*x^3 + 17*x^2 + 6*x + 1)/(2*x^3 - x + 3)

f = 
 $\frac{3 x^{3} + 17 x^{2} + 6 x + 1}{2 x^{3} - x + 3}$

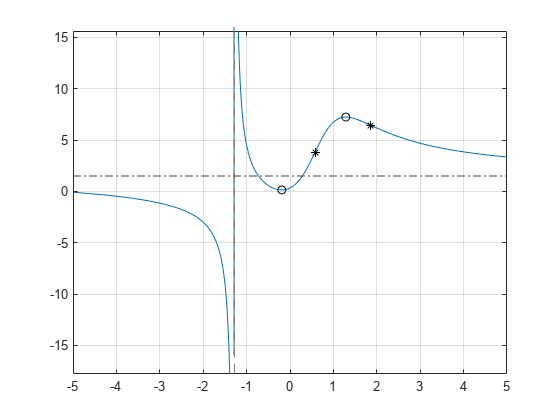
Plotting this expression shows that the expression has horizontal and vertical asymptotes, a local minimum between -1 and 0, and a local maximum between 1 and 2:

fplot(f)
grid

Figure contains an axes object. The axes object contains an object of type functionline.

To find the horizontal asymptote, compute the limits of f for x approaching positive and negative infinities. The horizontal asymptote is y = 3/2:

lim_left = limit(f, x, -inf)

lim_left = 
 $\frac{3}{2}$

lim_right = limit(f, x, inf)

lim_right = 
 $\frac{3}{2}$

Add this horizontal asymptote to the plot:

hold on
plot(xlim, [lim_right lim_right], 'LineStyle', '-.', 'Color', [0.25 0.25 0.25])

Figure contains an axes object. The axes object contains 2 objects of type functionline, line.

To find the vertical asymptote of f, find the poles of f:

pole_pos = poles(f, x)

pole_pos = 
 $- \frac{1}{6 {(\frac{3}{4} - \frac{\sqrt{241} \sqrt{432}}{432})}^{1 / 3}} - {(\frac{3}{4} - \frac{\sqrt{241} \sqrt{432}}{432})}^{1 / 3}$

Approximate the exact solution numerically by using the double function:

double(pole_pos)

ans = 
-1.2896

Now find the local minimum and maximum of f. If a point is a local extremum (either minimum or maximum), the first derivative of the expression at that point is equal to zero. Compute the derivative of f using diff:

g = diff(f, x)

g = 
 $\frac{9 x^{2} + 34 x + 6}{2 x^{3} - x + 3} - \frac{(6 x^{2} - 1) (3 x^{3} + 17 x^{2} + 6 x + 1)}{{(2 x^{3} - x + 3)}^{2}}$

To find the local extrema of f, solve the equation g == 0:

g0 = solve(g, x)

g0 = 
 $\begin{array}{l} (\begin{array}{c} \frac{\sqrt{σ_{2}}}{6 {σ_{3}}^{1 / 6}} - σ_{1} - \frac{15}{68} \\ \frac{\sqrt{σ_{2}}}{6 {σ_{3}}^{1 / 6}} + σ_{1} - \frac{15}{68} \end{array}) \\ where \\ σ_{1} = \frac{\sqrt{\frac{337491 \sqrt{6} \sqrt{\frac{3 \sqrt{3} \sqrt{178939632355}}{9826} + \frac{2198209}{9826}}}{39304} + \frac{2841 {σ_{3}}^{1 / 3} \sqrt{σ_{2}}}{578} - 9 {σ_{3}}^{2 / 3} \sqrt{σ_{2}} - \frac{361 \sqrt{σ_{2}}}{289}}}{6 {σ_{3}}^{1 / 6} {σ_{2}}^{1 / 4}} \\ σ_{2} = \frac{2841 {σ_{3}}^{1 / 3}}{1156} + 9 {σ_{3}}^{2 / 3} + \frac{361}{289} \\ σ_{3} = \frac{\sqrt{3} \sqrt{178939632355}}{176868} + \frac{2198209}{530604} \end{array}$

Approximate the exact solution numerically by using the double function:

double(g0)

ans = 2×1

   -0.1892
    1.2860

The expression f has a local maximum at x = 1.286 and a local minimum at x = -0.189. Obtain the function values at these points using subs:

f0 = subs(f,x,g0)

f0 = 
 $\begin{array}{l} (\begin{array}{c} \frac{3 σ_{2} - 17 {(σ_{5} - σ_{6} + \frac{15}{68})}^{2} - σ_{4} + σ_{1} + \frac{11}{34}}{σ_{6} + 2 σ_{2} - σ_{5} - \frac{219}{68}} \\ - \frac{σ_{4} + 17 {(σ_{6} + σ_{5} - \frac{15}{68})}^{2} + 3 σ_{3} + σ_{1} - \frac{11}{34}}{σ_{6} - 2 σ_{3} + σ_{5} - \frac{219}{68}} \end{array}) \\ where \\ σ_{1} = \frac{σ_{7}}{{σ_{9}}^{1 / 6} {σ_{8}}^{1 / 4}} \\ σ_{2} = {(σ_{5} - σ_{6} + \frac{15}{68})}^{3} \\ σ_{3} = {(σ_{6} + σ_{5} - \frac{15}{68})}^{3} \\ σ_{4} = \frac{\sqrt{σ_{8}}}{{σ_{9}}^{1 / 6}} \\ σ_{5} = \frac{σ_{7}}{6 {σ_{9}}^{1 / 6} {σ_{8}}^{1 / 4}} \\ σ_{6} = \frac{\sqrt{σ_{8}}}{6 {σ_{9}}^{1 / 6}} \\ σ_{7} = \sqrt{\frac{337491 \sqrt{6} \sqrt{\frac{3 \sqrt{3} \sqrt{178939632355}}{9826} + \frac{2198209}{9826}}}{39304} + \frac{2841 {σ_{9}}^{1 / 3} \sqrt{σ_{8}}}{578} - 9 {σ_{9}}^{2 / 3} \sqrt{σ_{8}} - \frac{361 \sqrt{σ_{8}}}{289}} \\ σ_{8} = \frac{2841 {σ_{9}}^{1 / 3}}{1156} + 9 {σ_{9}}^{2 / 3} + \frac{361}{289} \\ σ_{9} = \frac{\sqrt{3} \sqrt{178939632355}}{176868} + \frac{2198209}{530604} \end{array}$

Approximate the exact solution numerically by using the double function on the variable f0:

double(f0)

ans = 2×1

    0.1427
    7.2410

Add point markers to the graph at the extrema:

plot(g0, f0, 'ok')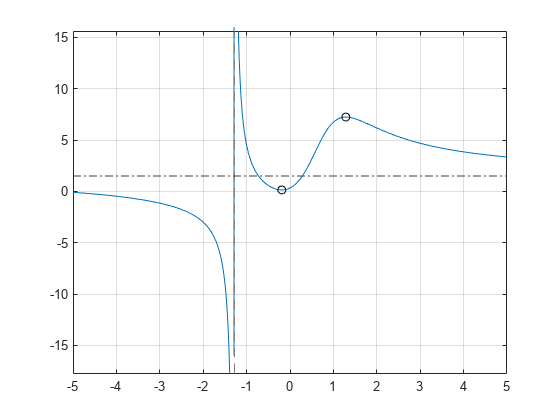

Figure contains an axes object. The axes object contains 3 objects of type functionline, line. One or more of the lines displays its values using only markers

Second Derivatives: Finding Inflection Points

Computing the second derivative lets you find inflection points of the expression. The most efficient way to compute second or higher-order derivatives is to use the parameter that specifies the order of the derivative:

h = diff(f, x, 2)

h = 
 $\begin{array}{l} \frac{18 x + 34}{σ_{1}} - \frac{2 (6 x^{2} - 1) (9 x^{2} + 34 x + 6)}{{σ_{1}}^{2}} - \frac{12 x σ_{2}}{{σ_{1}}^{2}} + \frac{2 {(6 x^{2} - 1)}^{2} σ_{2}}{{σ_{1}}^{3}} \\ where \\ σ_{1} = 2 x^{3} - x + 3 \\ σ_{2} = 3 x^{3} + 17 x^{2} + 6 x + 1 \end{array}$

Now simplify that result:

h = simplify(h)

h = 
 $\frac{2 (68 x^{6} + 90 x^{5} + 18 x^{4} - 699 x^{3} - 249 x^{2} + 63 x + 172)}{{(2 x^{3} - x + 3)}^{3}}$

To find inflection points of f, solve the equation h = 0. Here, use the numeric solver vpasolve to calculate floating-point approximations of the solutions:

h0 = vpasolve(h, x)

h0 = 
 $(\begin{array}{c} 0.57871842655441748319601085860196 \\ 1.8651543689917122385037075917613 \\ - 1.4228127856020972275345064554049 - 1.8180342567480118987898749770461 i \\ - 1.4228127856020972275345064554049 + 1.8180342567480118987898749770461 i \\ - 0.46088831805332057449182335801198 + 0.47672261854520359440077796751805 i \\ - 0.46088831805332057449182335801198 - 0.47672261854520359440077796751805 i \end{array})$

The expression f has two inflection points: x = 1.865 and x = 0.579. Note that vpasolve also returns complex solutions. Discard those:

h0(imag(h0)~=0) = []

h0 = 
 $(\begin{array}{c} 0.57871842655441748319601085860196 \\ 1.8651543689917122385037075917613 \end{array})$

Add markers to the plot showing the inflection points:

plot(h0, subs(f,x,h0), '*k')
hold off

Figure contains an axes object. The axes object contains 4 objects of type functionline, line. One or more of the lines displays its values using only markers