Find Asymptotes, Critical, and Inflection Points

Define a Function

The function in this example is

First, create the function.

syms x
num = 3*x^2 + 6*x -1;
denom = x^2 + x - 3;
f = num/denom

f = 
$$\frac{3\hspace{0.17em}{x}^2+6\hspace{0.17em}x-1}{x^2+x-3}$$

Plot the function by using fplot. The fplot function automatically shows vertical asymptotes.

fplot(f)

Find Asymptotes

To find the horizontal asymptote of $$f$$ mathematically, take the limit of $$f$$ as $$x$$ approaches positive infinity.

limit(f,Inf)

ans = $$3$$

The limit as $$x$$ approaches negative infinity is also 3. This result means the line $$y=3$$ is a horizontal asymptote to $$f$$.

To find the vertical asymptotes of $$f$$, set the denominator equal to 0 and solve it.

roots = solve(denom)

roots = 
$$\left(\begin{array}{c}-\frac{\sqrt{13}}{2}-\frac{1}{2}\\ \frac{\sqrt{13}}{2}-\frac{1}{2}\end{array}\right)$$

roots indicates that the vertical asymptotes are the lines

and

$\mathit{x}=\frac{-1+\sqrt{13}}{2}$.

Find Maximum and Minimum

You can see from the graph that $$f$$ has a local maximum between the points $$x=–2$$ and $$x=0$$. It also has a local minimum between $$x=–6$$ and $$x=–2$$. To find the $$x$$-coordinates of the maximum and minimum, first take the derivative of $$f$$.

f1 = diff(f)

f1 = 
$$\frac{6\hspace{0.17em}x+6}{x^2+x-3}-\frac{\left(2\hspace{0.17em}x+1\right)\hspace{0.17em}\left(3\hspace{0.17em}{x}^2+6\hspace{0.17em}x-1\right)}{{\left(x^2+x-3\right)}^2}$$

To simplify this expression, enter the following.

f1 = simplify(f1)

f1 = 
$$-\frac{3\hspace{0.17em}{x}^2+16\hspace{0.17em}x+17}{{\left(x^2+x-3\right)}^2}$$

Next, set the derivative equal to 0 and solve for the critical points.

crit_pts = solve(f1)

crit_pts = 
$$\left(\begin{array}{c}-\frac{\sqrt{13}}{3}-\frac{8}{3}\\ \frac{\sqrt{13}}{3}-\frac{8}{3}\end{array}\right)$$

As the graph of $$f$$ shows, the function has a local minimum at

and a local maximum at

${\mathit{x}}_1=\frac{-8+\sqrt{13}}{3}$.

Plot the maximum and minimum of f.

fplot(f)
hold on
plot(double(crit_pts), double(subs(f,crit_pts)),'ro')
title('Maximum and Minimum of f')
text(-4.8,5.5,'Local minimum')
text(-2,4,'Local maximum')
hold off

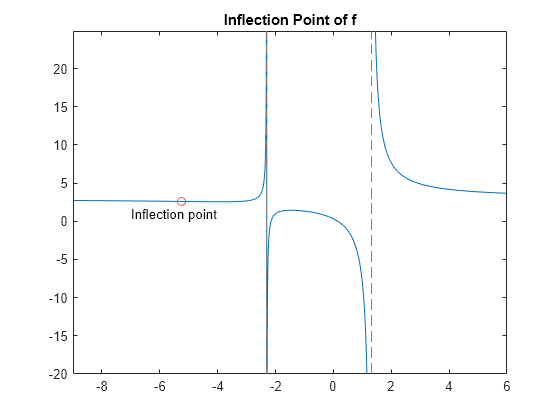
Find Inflection Point

To find the inflection point of $$f$$, set the second derivative equal to 0 and solve for this condition.

f2 = diff(f1);
inflec_pt = solve(f2,'MaxDegree',3);
double(inflec_pt)

ans = 3×1 complex

  -5.2635 + 0.0000i
  -1.3682 - 0.8511i
  -1.3682 + 0.8511i

In this example, only the first element is a real number, so this is the only inflection point. MATLAB® does not always return the roots to an equation in the same order.

Instead of selecting the real root by indexing into inter_pt, identify the real root by determining which roots have a zero-valued imaginary part.

idx = imag(double(inflec_pt)) == 0;
inflec_pt = inflec_pt(idx)

inflec_pt = 
$$-\frac{13}{9\hspace{0.17em}{\left(\frac{169}{54}-\frac{\sqrt{2197}}{18}\right)}^{1/3}}-{\left(\frac{169}{54}-\frac{\sqrt{2197}}{18}\right)}^{1/3}-\frac{8}{3}$$

Plot the inflection point. The extra argument [-9 6] in fplot extends the range of $$x$$ values in the plot so that you can see the inflection point more clearly, as the figure shows.

fplot(f,[-9 6])
hold on
plot(double(inflec_pt), double(subs(f,inflec_pt)),'ro')
title('Inflection Point of f')
text(-7,1,'Inflection point')
hold off