Prime Factorizations

This example shows how to use some elementary functions on sym objects using the Symbolic Math Toolbox™.

The built-in integer types of MATLAB® are suitable for integers smaller than 2^64. However, we want to carry out statistical investigations on prime factorizations of larger integers. To do this, we use symbolic integers because their size is unlimited. Investigate the integers between $N_{0} + 1$ and $N_{0} + 100$ , where $N_{0} = 3 * 1 0^{23}$ . The built-in data types cannot store such values exactly. Thus, wrap the innermost number with sym to use symbolic representation in the calculations. This avoids rounding or overflow errors:

N0 = 3*sym(10)^23;
disp(['Roundng error for doubles: ' char(3*10^23 - N0)]);

Roundng error for doubles: -25165824

disp(['Overflow error for integers: ' char(3*uint64(10)^23 - N0)]);

Overflow error for integers: -299981553255926290448385

In arithmetical operations, symbolic numbers can be combined with doubles, and the conversion takes place before the operation. Thus, the following definition cannot cause rounding errors:

A = N0 + (1:100);

Compute the prime factorizations of the elements of A using factor. The number of prime factors differs. Arrays cannot contain vectors of different lengths, but cell arrays can. To avoid memory re-allocations, initialize the cell array first, then compute the factorizations in a loop:

Bcell = cell(1, 100);
for i=1:100
   Bcell{i} = factor(A(i)); 
end

A more efficient approach is to use arrayfun. Setting UniformOutput to false returns the result as a cell array.

Bcell = arrayfun(@factor, A, 'UniformOutput', false);

For example, the first prime factorizations are:

Bcell{1:5}

ans =  $(\begin{array}{c} 13 & 43 & 233 & 2303316007278478583 \end{array})$

ans =  $(\begin{array}{c} 2 & 17 & 173 & 991 & 1223 & 244939 & 171805943 \end{array})$

ans =  $(\begin{array}{c} 3 & 11 & 47 & 139 & 2531 & 549797184491917 \end{array})$

ans =  $(\begin{array}{c} 2 & 2 & 330131 & 2953837 & 76910994983 \end{array})$

ans =  $(\begin{array}{c} 5 & 6271 & 2650266823 & 3610146697 \end{array})$

Obtain the largest prime factor using max. Note that if the output consists of sym objects, the option UniformOutput always has to be set to false even if the output is uniform.

Mcell = cellfun(@max, Bcell, 'UniformOutput', false);

For example, the first maximal prime factors are:

Mcell{1:5}

ans =  $2303316007278478583$

ans =  $171805943$

ans =  $549797184491917$

ans =  $76910994983$

ans =  $3610146697$

Convert the cell array to a symbolic vector, and investigate the ratio of the lengths of the largest prime factor and the number as a whole. You can apply arithmetical operations elementwise to symbolic vectors, in the same way as for doubles. Note that most statistical functions require their arguments to be double-precision numbers.

M = [Mcell{:}];
histogram(double(log(M)./log(A)), 20);
title('Ratio of lengths of the largest prime factor and the number');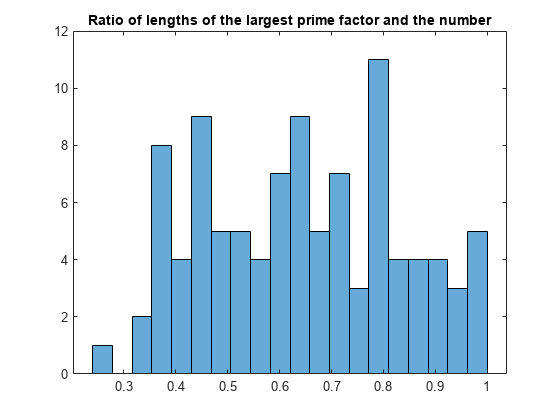

Figure contains an axes object. The axes object with title Ratio of lengths of the largest prime factor and the number contains an object of type histogram.

In the same way, now investigate the distribution of the number of prime factors. Here, the result contains uniform numeric data. Therefore, you do not need to set UniformOutput to false.

omega = cellfun(@numel, Bcell);
histogram(omega);
title('Number of prime factors');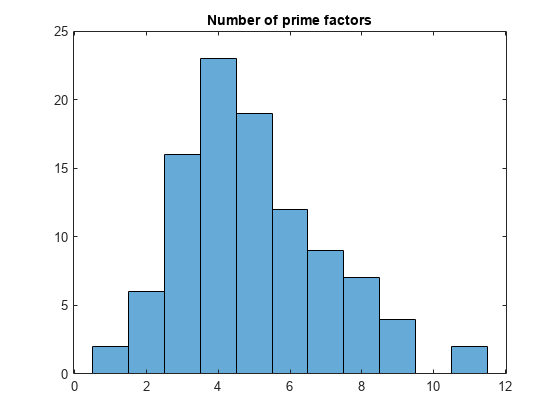

Figure contains an axes object. The axes object with title Number of prime factors contains an object of type histogram.

The interval under investigation contains two prime numbers:

A(omega == 1)

ans =  $(\begin{array}{c} 300000000000000000000037 & 300000000000000000000049 \end{array})$

We check that the maximal prime factors are about equally often in the residue classes 1 and 3 modulo 4. Note that equations of sym objects are symbolic objects themselves and not logical values; we have to convert them before we can sum them:

sum(logical(mod(M, 4) == 1))

ans = 
49

sum(logical(mod(M, 4) == 3))

ans = 
51