矩阵旋转和变换

此示例说明了如何使用 Symbolic Math Toolbox™ 和矩阵在三维空间中进行旋转和变换。

定义并绘制参数曲面

按如下所示定义参数曲面 x(u,v)、y(u,v)、z(u,v)。

syms u v
x = cos(u)*sin(v);
y = sin(u)*sin(v);
z = cos(v)*sin(v);

使用 fsurf 绘制曲面。

fsurf(x,y,z)
axis equal

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.

创建旋转矩阵

创建 3×3 矩阵 Rx、Ry 和 Rz，分别表示绕 x 轴、y 轴和 z 轴旋转 t 度的平面旋转。

syms t

Rx = [1 0 0; 0 cos(t) -sin(t); 0 sin(t) cos(t)]

Rx = 
 $(\begin{array}{c} 1 & 0 & 0 \\ 0 & \cos (t) & - \sin (t) \\ 0 & \sin (t) & \cos (t) \end{array})$

Ry = [cos(t) 0 sin(t); 0 1 0; -sin(t) 0 cos(t)]

Ry = 
 $(\begin{array}{c} \cos (t) & 0 & \sin (t) \\ 0 & 1 & 0 \\ - \sin (t) & 0 & \cos (t) \end{array})$

Rz = [cos(t) -sin(t) 0; sin(t) cos(t) 0; 0 0 1]

Rz = 
 $(\begin{array}{c} \cos (t) & - \sin (t) & 0 \\ \sin (t) & \cos (t) & 0 \\ 0 & 0 & 1 \end{array})$

在三维空间中绕每个轴旋转

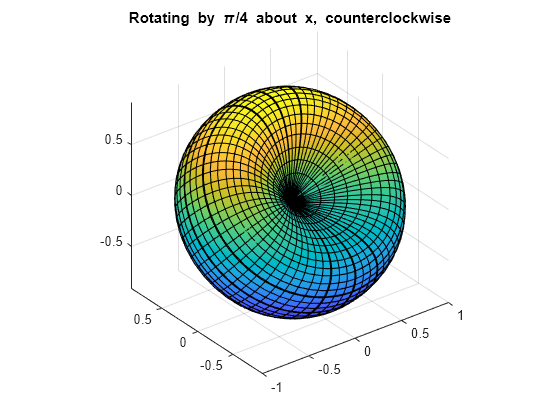
首先，将曲面绕 x 轴逆时针旋转 45 度。

xyzRx = Rx*[x;y;z];
Rx45 = subs(xyzRx, t, pi/4);

fsurf(Rx45(1), Rx45(2), Rx45(3))
title('Rotating by \pi/4 about x, counterclockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 4 about x, counterclockwise contains an object of type parameterizedfunctionsurface.

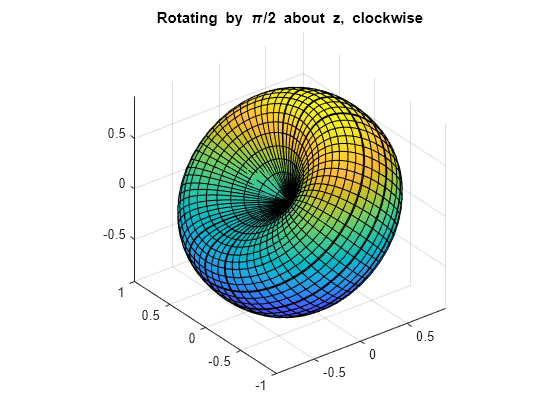
绕 z 轴顺时针旋转 90 度。

xyzRz = Rz*Rx45;
Rx45Rz90 = subs(xyzRz, t, -pi/2);

fsurf(Rx45Rz90(1), Rx45Rz90(2), Rx45Rz90(3))
title('Rotating by \pi/2 about z, clockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 2 about z, clockwise contains an object of type parameterizedfunctionsurface.

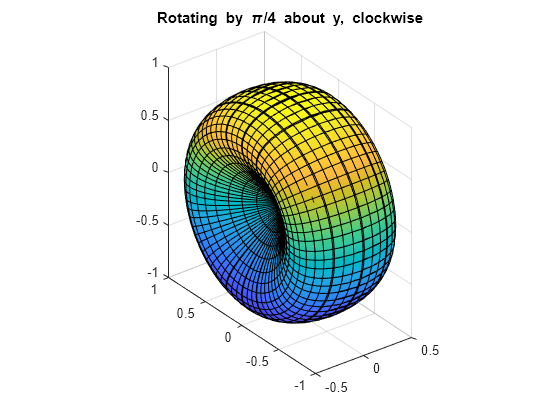
绕 y 轴顺时针旋转 45 度。

xyzRy = Ry*Rx45Rz90;
Rx45Rz90Ry45 = subs(xyzRy, t, -pi/4);

fsurf(Rx45Rz90Ry45(1), Rx45Rz90Ry45(2), Rx45Rz90Ry45(3))
title('Rotating by \pi/4 about y, clockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 4 about y, clockwise contains an object of type parameterizedfunctionsurface.

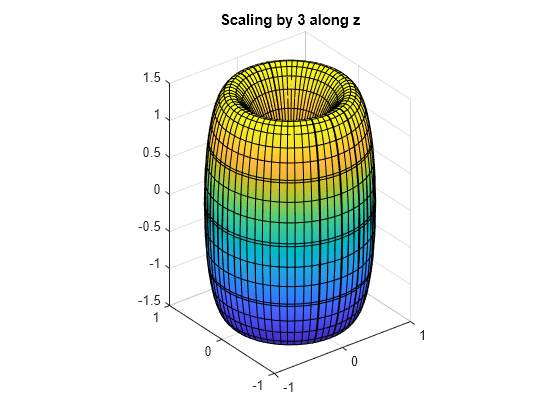
缩放和旋转

沿 z 轴将曲面拉伸 3 倍。可以将表达式 z 乘以 3，即 z = 3*z。更通用的方法是创建一个缩放矩阵，然后将缩放矩阵与坐标向量相乘。

S = [1 0 0; 0 1 0; 0 0 3];
xyzScaled = S*[x; y; z]

xyzScaled = 
 $(\begin{array}{c} \cos (u) \sin (v) \\ \sin (u) \sin (v) \\ 3 \cos (v) \sin (v) \end{array})$

fsurf(xyzScaled(1), xyzScaled(2), xyzScaled(3))
title('Scaling by 3 along z')
axis equal

Figure contains an axes object. The axes object with title Scaling by 3 along z contains an object of type parameterizedfunctionsurface.

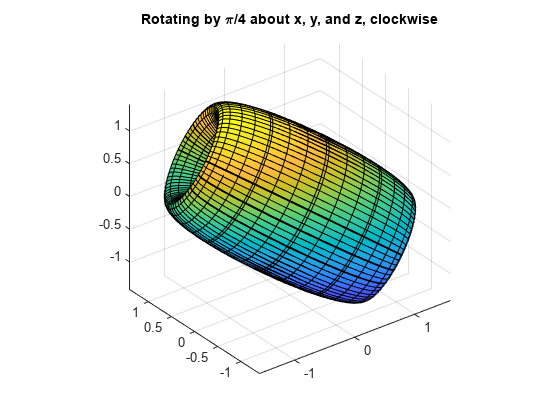
按 z 轴、y 轴、x 轴的顺序，将缩放后的曲面绕 x 轴、y 轴和 z 轴顺时针旋转 45 度。该变换的旋转矩阵如下。

R = Rx*Ry*Rz

R = 
 $\begin{array}{l} (\begin{array}{c} {\cos (t)}^{2} & - \cos (t) \sin (t) & \sin (t) \\ σ_{1} & {\cos (t)}^{2} - {\sin (t)}^{3} & - \cos (t) \sin (t) \\ {\sin (t)}^{2} - {\cos (t)}^{2} \sin (t) & σ_{1} & {\cos (t)}^{2} \end{array}) \\ where \\ σ_{1} = \cos (t) {\sin (t)}^{2} + \cos (t) \sin (t) \end{array}$

使用该旋转矩阵求出新的坐标。

xyzScaledRotated = R*xyzScaled;
xyzSR45 = subs(xyzScaledRotated, t, -pi/4);

绘制曲面。

fsurf(xyzSR45(1), xyzSR45(2), xyzSR45(3))
title('Rotating by \pi/4 about x, y, and z, clockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 4 about x, y, and z, clockwise contains an object of type parameterizedfunctionsurface.

检查旋转矩阵 `R` 的性质

旋转矩阵是正交矩阵。因此，R 的转置矩阵即是其逆矩阵，并且 R 的行列式为 1。

simplify(R.'*R)

ans = 
 $(\begin{array}{c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array})$

simplify(det(R))

ans =  $1$