1-D Fractional Brownian Motion Synthesis

This example shows how to generate a fractional Brownian motion signal using the wfbm function.

A fractional Brownian motion (fBm) is a continuous-time Gaussian process depending on the Hurst parameter 0 < H < 1. It generalizes the ordinary Brownian motion corresponding to H = 0.5 and whose derivative is white noise. The fBm is self-similar in distribution and the variance of the increments is given by

Var(fBm(t) - fBm(s)) = v abs(t-s)^(2H),

where v is a positive constant. The fBm exhibits long-range dependence for H > 0.5 and short or intermediate dependence for H < 0.5.

For purposes of reproducibility, set the random seed to the default value. Generate fractional Brownian motion with length 1000 for H = 0.3. Plot the result.

rng default
H = 0.3;
len = 1000;
fBm03 = wfbm(H,len,'plot');

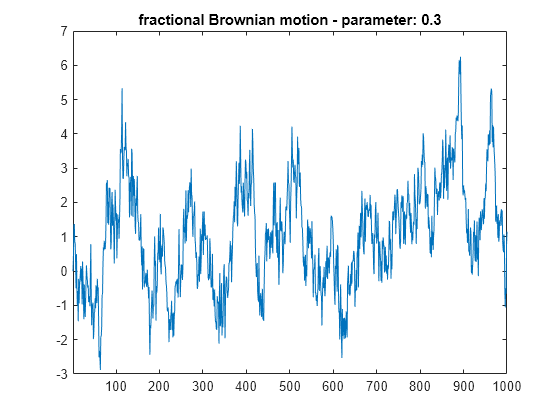
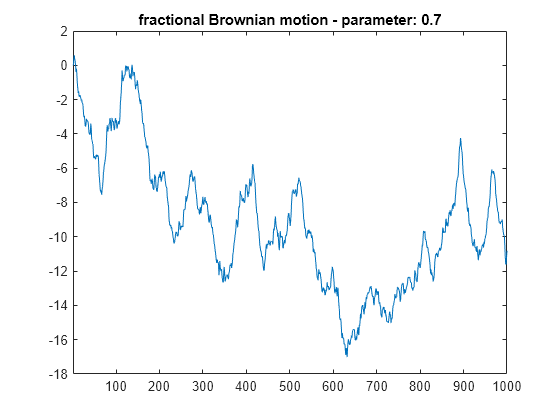
Generate fractional Brownian motion with length 1000 for H = 0.7. Plot the result. Because H > 0.5, the fractional Brownian motion exhibits a stronger low-frequency component and has, locally, less irregular behavior.

rng default
H = 0.7;
fBm07 = wfbm(H,len,'plot');

Confirm the previous syntax is equivalent to generating fractional Brownian motion using the orthogonal db10 wavelet and six reconstruction steps.

rng default
w = 'db10';
ns = 6;
fBm07x = wfbm(H,len,w,ns);
max(abs(fBm07-fBm07x))

ans = 
0