Wavelets and Vanishing Moments

This example shows how the number of vanishing moments can affect wavelet coefficients.

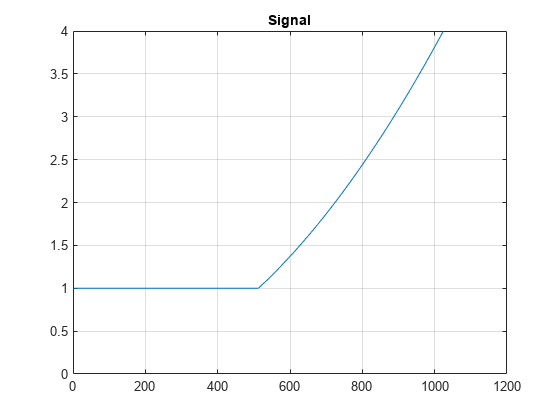
Create a signal defined over the interval $0\le \mathit{x}\le 2$. The signal is constant over the interval $0\le \mathit{x}<1$ and quadratic over the interval $1\le \mathit{x}\le 2$. Plot the signal.

n = 1024;
x = linspace(0,2,n);
sig = zeros(1,n);
ind0 = (0<=x)&(x<1);
ind1 = (1<=x)&(x<=2);
sig(ind0) = 1;
sig(ind1) = x(ind1).^2;
plot(sig)
ylim([0 4])
grid on
title('Signal')

Compute a single-level wavelet decomposition of the signal using the db1 wavelet. This wavelet has one vanishing moment. Plot the approximation coefficients and wavelet coefficients.

[a1,d1] = dwt(sig,'db1');
figure
subplot(2,1,1)
plot(a1)
ylim([0 6])
grid on
title('Approximation Coefficients - db1')
subplot(2,1,2)
plot(d1)
ylim([-6e-3 0])
grid on
title('Wavelet Coefficients - db1')

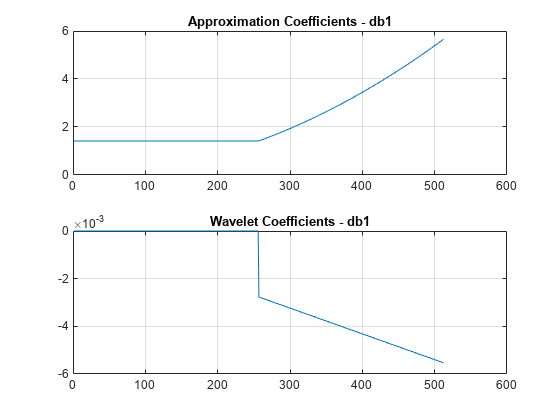
The wavelet coefficients corresponding with the constant portion of the signal are approximately 0. The magnitude of the wavelet coefficients corresponding with the quadratic portion of the signal are increasing. Because the db1 wavelet has one vanishing moment, the wavelet is not orthogonal to the quadratic portion of the signal.

Compute a single-level wavelet decomposition of the signal using the db3 wavelet. This wavelet has three vanishing moments. Plot the approximation coefficients and wavelet coefficients.

[a2,d2] = dwt(sig,'db3');
figure
subplot(2,1,1)
plot(a2)
ylim([0 6])
grid on
title('Approximation Coefficients - db3')
subplot(2,1,2)
plot(d2)
grid on
title('Wavelet Coefficients - db3')

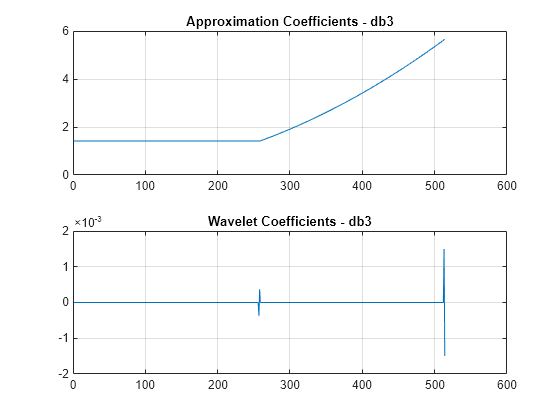
The wavelet coefficients corresponding with the constant portion of the signal are approximately 0. The spike in the middle corresponds to where the constant and quadratic pieces of the signal meet. The spike at the end is a boundary effect. The magnitude of the wavelet coefficients corresponding with the quadratic portion of the signal are approximately 0. Because the db3 wavelet has three vanishing moments, the wavelet is orthogonal to the quadratic part of the signal.

See Also

waveinfo