Wavelet Analysis for 3-D Data
This example shows how to analyze 3-D data using the three-dimensional wavelet analysis tool, and how to display low-pass and high-pass components along a given slice. The example focuses on magnetic resonance images.
A key feature of this analysis is to track the optimal, or at least a good, wavelet-based sparsity of the image which is the lowest percentage of transform coefficients sufficient for diagnostic-quality reconstruction.
To illustrate this, we keep the approximation of a 3-D MRI to show the complexity reduction. The result can be improved if the images were transformed and reconstructed from the largest transform coefficients where the definition of the quality is assessed by medical specialists.
We will see that Wavelet transform for brain images allows efficient and accurate reconstructions involving only 5-10% of the coefficients.
Load and Display 3-D MRI Data
First, load the wmri.mat file which is built from the MRI data set that comes with MATLAB®.
load wmriWe now display some slices along the Z-orientation of the original brain data.
map = pink(90); idxImages = 1:3:size(X,3); figure('DefaultAxesXTick',[],'DefaultAxesYTick',[],... 'DefaultAxesFontSize',8,'Color','w') colormap(map) for k = 1:9 j = idxImages(k); subplot(3,3,k) image(X(:,:,j)) xlabel(['Z = ' int2str(j)]) if k==2 title('Some Slices Along Z-orientation of Original Brain Data') end end

We now switch to the Y-orientation slice.
perm = [1 3 2]; XP = permute(X,perm); figure('DefaultAxesXTick',[],'DefaultAxesYTick',[],... 'DefaultAxesFontSize',8,'Color','w') colormap(map) for k = 1:9 j = idxImages(k); subplot(3,3,k) image(XP(:,:,j)) xlabel(['Y = ' int2str(j)]) if k==2 title('Some Slices Along Y-orientation') end end

clear XPMultilevel 3-D Wavelet Decomposition
Compute the wavelet decomposition of the 3-D data at level 3.
n = 3; % Decomposition Level w = 'sym4'; % Near Symmetric Wavelet WT = wavedec3(X,n,w); % Multilevel 3-D Wavelet Decomposition.
Multilevel 3-D Wavelet Reconstruction
Reconstruct from coefficients the approximations and details for levels 1 to 3.
A = cell(1,n); D = cell(1,n); for k = 1:n A{k} = waverec3(WT,'a',k); % Approximations (lowpass components) D{k} = waverec3(WT,'d',k); % Details (highpass components) end
Check for perfect reconstruction.
err = zeros(1,n); for k = 1:n E = double(X)-A{k}-D{k}; err(k) = max(abs(E(:))); end disp(err)
1.0e-09 *
0.3044 0.3044 0.3044
Display Lowpass and Highpass Components
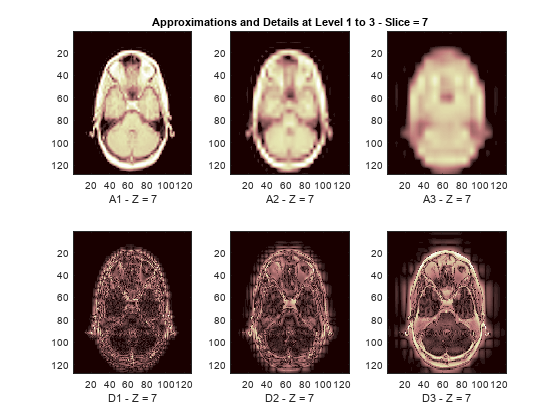
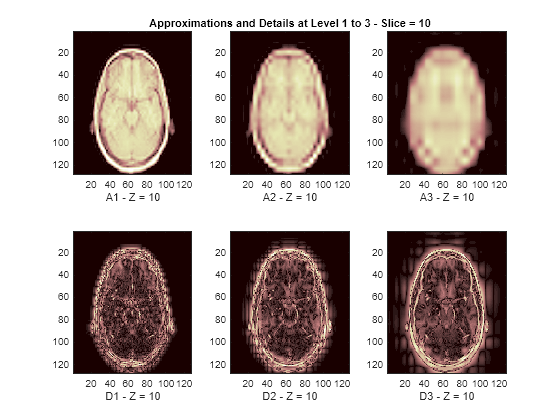
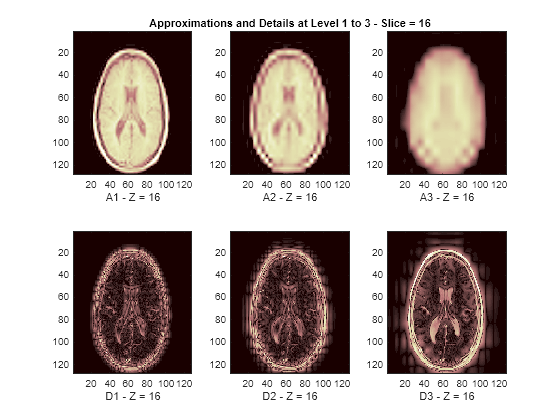
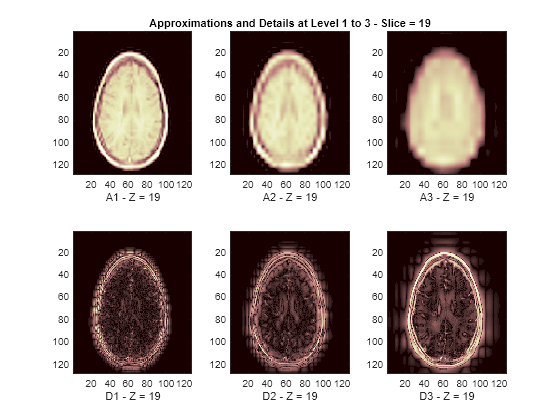
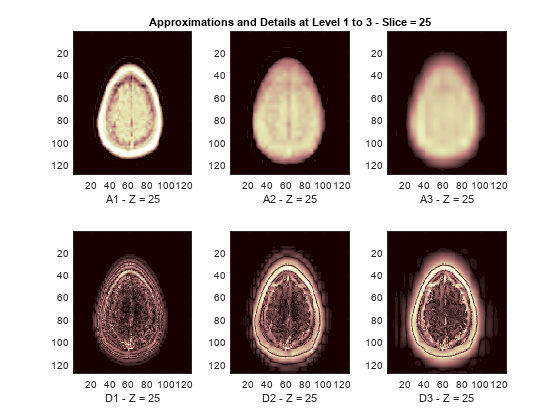
The reconstructed approximations and details along the Z-orientation are displayed below.
nbIMG = 6; idxImages_New = [1 7 10 16 19 25]; for ik = 1:nbIMG j = idxImages_New(ik); figure('DefaultAxesXTick',[],'DefaultAxesYTick',[],... 'DefaultAxesFontSize',8,'Color','w') colormap(map) for k = 1:n labstr = [int2str(k) ' - Z = ' int2str(j)]; subplot(2,n,k) image(A{k}(:,:,j)) xlabel(['A' labstr]) if k==2 title(['Approximations and Details at Level 1 to 3 - Slice = ' num2str(j)]) end subplot(2,n,k+n) imagesc(abs(D{k}(:,:,j))) xlabel(['D' labstr]) end end

3-D Display of Original Data and Approximation at Level 2
The size of the 3-D original array X is (128 x 128 x 27) = 442368. We can use a 3-D display to show it.
figure('DefaultAxesXTick',[],'DefaultAxesYTick',[],... 'DefaultAxesFontSize',8,'Color','w') XR = X; Ds = smooth3(XR); hiso = patch(isosurface(Ds,5),'FaceColor',[1,.75,.65],'EdgeColor','none'); hcap = patch(isocaps(XR,5),'FaceColor','interp','EdgeColor','none'); colormap(map) daspect(gca,[1,1,.4]) lightangle(305,30); lighting gouraud isonormals(Ds,hiso) hcap.AmbientStrength = .6; hiso.SpecularColorReflectance = 0; hiso.SpecularExponent = 50; ax = gca; ax.View = [215,30]; ax.Box = 'On'; axis tight title('Original Data')

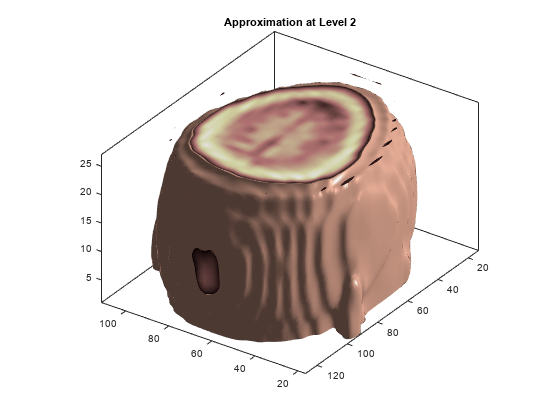
The 3-D array of the coefficients of approximation at level 2, whose size is (22 x 22 x 9) = 4356, is less than 1% the size of the original data. With these coefficients, we can reconstruct A2, the approximation at level 2, which is a kind of compression of the original 3-D array. A2 can also be shown using a 3-D display.
figure('DefaultAxesXTick',[],'DefaultAxesYTick',[],... 'DefaultAxesFontSize',8,'Color','w') XR = A{2}; Ds = smooth3(XR); hiso = patch(isosurface(Ds,5),'FaceColor',[1,.75,.65],'EdgeColor','none'); hcap = patch(isocaps(XR,5),'FaceColor','interp','EdgeColor','none'); colormap(map) daspect(gca,[1,1,.4]) lightangle(305,30); lighting gouraud isonormals(Ds,hiso) hcap.AmbientStrength = .6; hiso.SpecularColorReflectance = 0; hiso.SpecularExponent = 50; ax = gca; ax.View = [215,30]; ax.Box = 'On'; axis tight title('Approximation at Level 2')
Summary
This example shows how to use 3-D wavelet functions to analyze 3-D data.