Technical Articles

Best Practices for Converting MATLAB Code to Fixed Point

By Harshita Bhurat, Tom Bryan, and Julia Wall, MathWorks

When converting a floating-point implementation to fixed point, engineers must identify optimal fixed-point data types that meet the constraints of embedded hardware while satisfying system requirements for numerical accuracy. Fixed-Point Designer™ helps you develop fixed-point algorithms and convert floating-point algorithms to fixed point by automatically proposing data types and fixed-point attributes and enabling comparisons of bit-true fixed-point simulation results with floating-point baselines.

This article outlines best practices for preparing MATLAB® code for conversion, converting MATLAB code to fixed point, and optimizing your algorithm for efficiency and performance. Whether you are designing fixed-point algorithms in MATLAB in preparation for hand-coding or converting to fixed point for code generation, these best practices will help you turn your generic MATLAB code into an efficient fixed-point implementation.

Prepare Code for Fixed-Point Conversion

There are three steps that you can take to ensure a smooth conversion process:

  • Separate your core algorithm from other code.
  • Prepare your code for instrumentation and acceleration.
  • Check the functions you use for fixed-point support.

Separate the Core Algorithm from Other MATLAB Code

Typically, an algorithm is accompanied by code that sets up input data and code that creates plots to verify the result. Since only the algorithmic code needs to be converted to fixed point, it is more efficient to structure the code so that a test file creates inputs, invokes the core algorithm, and plots the results, and algorithmic files perform the core processing (Table 1).

Original Code
% TEST INPUT 
x = randn(100,1); 

% ALGORITHM 
y = zeros(size(x)); 
y(1) = x(1); 
for n=2:length(x)
  y(n) = y(n-1) + x(n); 
end 

% VERIFY RESULTS 
yExpected = cumsum(x); 
plot(y-yExpected) 
title('Error')
Modified Code

Test file.

% TEST INPUT 
x = randn(100,1); 

% ALGORITHM 
y = cumulative_sum(x); 

% VERIFY RESULTS 
yExpected = cumsum(x); 
plot(y-yExpected) 
title('Error')

Algorithm file.

function y = cumulative_sum(x)
  y = zeros(size(x));
  y(1) = x(1);
  for n=2:length(x)
    y(n) = y(n-1) + x(n);
  end
end

Prepare Your Algorithmic Code for Instrumentation and Acceleration

Instrumentation and acceleration help streamline the conversion process. You can use Fixed-Point Designer to instrument your code and log minimum and maximum values of all named and intermediate variables. The tool can use these logged values to propose data types for use in the fixed-point code.

With Fixed-Point Designer you can also accelerate your fixed-point algorithms by creating a MEX file, and speed up the simulations needed to verify the fixed-point implementation against the original version.

Instrumentation and acceleration both rely on code generation technology, so before you can use them you must prepare your algorithms for code generation even if you do not plan to use MATLAB Coder™ or HDL Coder™ to generate the C or HDL code. First, identify functions or constructs in your MATLAB code not supported for code generation (see Language Support for a list of supported functions and objects).

There are two ways to automate this step:

  • Add the %#codegen pragma to the top of the MATLAB file containing your core algorithm code. This pragma instructs Code Analyzer to flag functions and constructs that are not included in the subset of the MATLAB language supported for code generation.
  • Use the Code Generation Readiness tool to produce a report that identifies calls to functions and the use of data types not supported for code generation.

Once you have prepared your algorithm for code generation, you can use Fixed-Point Designer to instrument and accelerate it. Use buildInstrumentedMex to enable instrumentation for logging minimum and maximum values of all named and intermediate variables, and use showInstrumentationResults to view a code generation report with proposed data types for use in the fixed-point code. Invoke fiaccel to translate your MATLAB algorithm to a MEX file and accelerate your fixed-point simulations.

Check for Fixed-Point Support for Functions Used in Your Algorithmic Code

If you identify a function that is not supported for fixed point, you have three options:

  • Replace the function with a fixed-point equivalent.
  • Write your own equivalent function.
  • Insulate the unsupported function with a cast to double at the input, and a cast back to a fixed-point type at the output.

You can then continue converting your code to fixed point, and return to the unsupported function when you have a suitable replacement (Table 2).

Original Code
 y = 1/exp(x);
Modified Code
 y = 1/exp(double(x));

Manage Data Types and Control Bit Growth

In a fixed-point implementation, fixed-point variables must remain fixed point, and not be inadvertently turned into doubles. It is also important to prevent bit growth. For example, consider the following line of code:

 y = y + x(n)

This statement overwrites y with the value of y + x(n). When you introduce fixed-point data types into your code, y may change data types when it is overwritten, potentially resulting in bit growth.

To preserve the data type of y use (:) = syntax (Table 3). This syntax, known as subscripted assignment, instructs MATLAB to retain the existing data type and array size of the overwritten variable. The statement y(:) = y + x(n) will cast the right-hand-side value into y's original data type and prevent bit growth.

Original Code
y = 0; 
for n=1:length(x) 
  y = y + x(n); 
end
Modified Code
y = 0; 
for n=1:length(x) 
  y(:) = y + x(n); 
end

Create a Types Table to Separate Data Type Definitions from Algorithmic Code

Separating data type definitions from algorithmic code makes it easier to compare fixed-point implementations and retarget your algorithm to a different device.

To apply this best practice, do the following:

  1. Use cast(x,'like',y) or zeros(m,n,'like',y) to cast a variable to your desired data type when it is first defined.
  2. Create a table of data type definitions, starting with the original data types used in your code—typically, double-precision floating-point, the default data type in MATLAB (Table 4a).
  3. Before converting to fixed point, add single data types to the types table to find type mismatches and other problems (Table 4b).
  4. Verify the connection by running the code connected to each table with different data types and comparing the results.
Original Code
% Algorithm 
n = 128; 
y = zeros(size(x));
Modified Code
% Algorithm 
T = mytypes('double'); 
n = cast(128,'like',T.n); 
y = zeros(size(x),'like',T.y); 

% Types Table 
function T = mytypes(dt) 
  switch(dt) 
    case 'double' 
      T.n = double([]); 
      T.y = double([]); 
  end 
end
Original Code
% Types 
Table function T = mytypes(dt) 
  switch(dt) 
    case 'double' 
      T.n = double([]); 
      T.y = double([]); 
  end 
end
Modified Code
function T = mytypes(dt) 
  switch(dt) 
    case 'double' 
      T.n = double([]); 
      T.y = double([]); 
    case 'single' 
      T.n = single([]); 
      T.y = single([]); 
  end 
end

Add Fixed-Point Entries to the Types Table

Once you have created a table of data type definitions, you can add fixed-point types based on your objectives for converting to fixed point. For example, if you plan to implement your algorithm in C, the word lengths for your fixed-point types will be constrained to a multiple of 16. On the other hand, if you plan to implement in HDL, the word length is not constrained.

To get a set of fixed-point type proposals for your code, use the Fixed-Point Designer commands buildInstrumentedMex and showInstrumentationResults (Table 5). You will need a set of test vectors that exercises the full range of types—the types proposed by Fixed-Point Designer are only as good as the test inputs. A long simulation run with a wide range of expected data will produce better proposals. Choose an initial set of fixed-point types from the proposals in the code generation report (Figure 1).

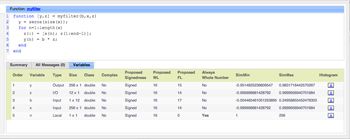
Figure 1. A code generation report produced by showInstrumentationResults with proposed data types for variables in the filtering algorithm.
Figure 1. A code generation report produced by showInstrumentationResults with proposed data types for variables in the filtering algorithm.

You can then adjust the proposed types as necessary (Tables 5 and 6).

Algorithm Code
function [y,z] = myfilter(b,x,z) 
  y = zeros(size(x)); 
  for n=1:length(x) 
    z(:) = [x(n); z(1:end-1)]; 
    y(n) = b * z; 
  end 
end
Test File
% Test inputs 
b = fir1(11,0.25); 
t = linspace(0,10*pi,256)'; 
x = sin((pi/16)*t.^2); % Linear chirp 
z = zeros(size(b')); 

% Build 
buildInstrumentedMex myfilter ... 
  -args {b,x,z} -histogram 

% Run 
[y,z] = myfilter_mex(b,x,z); 

% Show 
showInstrumentationResults myfilter_mex ... 
  -defaultDT numerictype(1,16) -proposeFL

Table 5. A filtering algorithm and test script for instrumenting and executing code and showing proposed fixed-point types for variables.

Algorithm Code
function [y,z] = myfilter(b,x,z,T) 
  y = zeros(size(x),'like',T.y); 
  for n=1:length(x) 
    z(:) = [x(n); z(1:end-1)]; 
    y(n) = b * z; 
  end 
end
Test File
% Test inputs 
b = fir1(11,0.25); 
t = linspace(0,10*pi,256)'; 
x = sin((pi/16)*t.^2); % Linear chirp 

% Cast inputs 
T = mytypes('fixed16'); 
b = cast(b,'like',T.b); 
x = cast(x,'like',T.x); 
z = zeros(size(b'),'like',T.x); 

% Run 
[y,z] = myfilter(b,x,z,T);
Types Tables
function T = mytypes(dt) 
  switch dt 
    case 'double' 
      T.b = double([]); 
      T.x = double([]); 
      T.y = double([]); 
    case 'fixed16' 
      T.b = fi([],true,16,15); 
      T.x = fi([],true,16,15); 
      T.y = fi([],true,16,14); 
  end 
end
 

Table 6. The test script and filtering algorithm from Table 4 updated with fixed-point data types.

Run your algorithm with the new fixed-point types and compare its output with the output of the baseline algorithm.

Optimize Data Types

Whether you select your own fixed-point data types or use those proposed by Fixed-Point Designer, look for opportunities to optimize the word lengths, fraction lengths, signedness, and possibly even the math modes (fimath). You can do this by using scaled doubles, viewing a histogram of variable values, or testing different types in your data type table.

Use Scaled Doubles to Detect Potential Overflows

Scaled doubles are hybrids of floating-point and fixed-point numbers. Fixed-Point Designer stores scaled doubles as doubles with the scaling, sign, and word length information retained. To use scaled doubles, set the data type override (DTO) property (Table 7).

DTO Setting Example
DTO set locally using numerictype
‘DataType’ property		 
>> T.a = fi([], 1, 16, 13,'DataType', 
'ScaledDouble');

>> a = cast(pi, 'like', T.a) 

a = 
  3.1416 

  DataTypeMode: Scaled double: binary point scaling 
    Signedness: Signed 
    WordLength: 16 
FractionLength: 13
DTO set globally using fipref
‘DataTypeOverride’ property		 
>> fipref('DataTypeOverride', 'ScaledDoubles'); 

>> T.a = fi([], 1, 16, 13); 

>> a = cast(pi, 'like', T.a) 

a = 
    3.1416 

  DataTypeMode: Scaled double: binary point scaling 
    Signedness: Signed 
    WordLength: 16 
FractionLength: 13

Table 7. Methods for setting the data type override property locally and globally.

Use buildInstrumentedMex to run your code and showInstrumentationResults to view the results. In the code generation report, values that would have overflowed are highlighted in red (Figure 2).

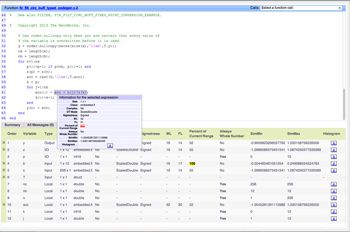
Figure 2. Code generation report showing overflows when using the Scaled Doubles type and the Histogram icon.
Figure 2. Code generation report showing overflows when using the Scaled Doubles type (left) and the Histogram icon (right).

Check the Distribution of Variable Values

You can use a histogram to identify data types with values that are within range, outside range, or below precision. Click the Histogram icon to launch the NumericTypeScope and view the distribution of values observed in your simulation for the selected variable (Figure 3).

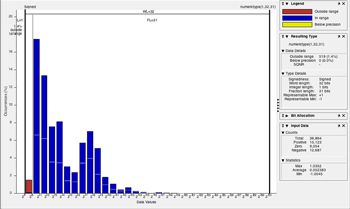
Figure 3. Histogram showing a distribution of variable values.
Figure 3. Histogram showing a distribution of variable values, with an overflow condition (“Outside range”) indicated in red.

Test Different Types in Your Data Type Table

You can add your own variations of fixed-point types to your types table (Table 8).

Algorithm Code
function [y,z] = myfilter(b,x,z,T) 
  y = zeros(size(x),'like',T.y); 
  for n=1:length(x) 
    z(:) = [x(n); z(1:end-1)]; 
    y(n) = b * z; 
  end 
end
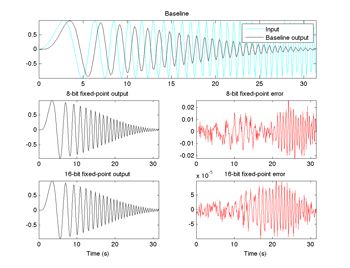
Test File
function mytest 
  % Test inputs 
  b = fir1(11,0.25); 
  t = linspace(0,10*pi,256)'; 
  x = sin((pi/16)*t.^2); % Linear chirp 

  % Run 
  y0 = entrypoint('double',b,x); 
  y8 = entrypoint('fixed8',b,x); 
  y16 = entrypoint('fixed16',b,x); 

  % Plot 
  subplot(3,1,1);plot(t,x,'c',t,y0,'k'); 
  legend('Input','Baseline output') 
  title('Baseline') 

  subplot(3,2,3);plot(t,y8,'k'); 
  title('8-bit fixed-point output') 
  subplot(3,2,4);plot(t,y0-double(y8),'r'); 
  title('8-bit fixed-point error') 

  subplot(3,2,5);plot(t,y16,'k'); 
  title('16-bit fixed-point output') 
  xlabel('Time (s)') 
  subplot(3,2,6);plot(t,y0-double(y16),'r'); 
  title('16-bit fixed-point error') 
  xlabel('Time (s)') 
end 

function [y,z] = entrypoint(dt,b,x) 
  T = mytypes(dt); 
  b = cast(b,'like',T.b); 
  x = cast(x,'like',T.x); 
  z = zeros(size(b'),'like',T.x); 
  [y,z] = myfilter(b,x,z,T); 
end
Types Tables
function T = mytypes(dt) 
  switch dt 
    case 'double' 
      T.b = double([]); 
      T.x = double([]); 
      T.y = double([]); 
    case 'fixed8' 
      T.b = fi([],true,8,7); 
      T.x = fi([],true,8,7); 
      T.y = fi([],true,8,6); 
    case 'fixed16' 
      T.b = fi([],true,16,15); 
      T.x = fi([],true,16,15); 
      T.y = fi([],true,16,14); 
  end 
end
 

Table 8. Test script for examining the effect of using different fixed-point data types in the types tables for a filtering function.

Compare results across iterations to verify the accuracy of your algorithm after each change (Figure 4).

Figure 4. Plots from the test script in Table 8 showing the output and error after converting to 8-bit and 16-bit fixed-point types.
Figure 4. Plots from the test script in Table 8 showing the output and error after converting to 8-bit and 16-bit fixed-point types.

Optimize Your Algorithm

There are three common ways to optimize your algorithm to improve performance and generate more efficient C code. You can:

  • Use fimath properties to improve the efficiency of generated code
  • Replace built-in functions with more efficient fixed-point implementations
  • Re-implement division operations

Use fimath Properties to Improve the Efficiency of Generated Code

When you use default fimath settings, extra code is generated to implement saturation overflow, nearest rounding, and full-precision arithmetic (Table 9a).

MATLAB Code
Code being compiled: 

function y = adder(a,b) 
  y = a + b; 
end 

With types defined with 
default fimath settings: 

T.a = fi([],1,16,0); 
T.b = fi([],1,16,0); 

a = cast(0,'like',T.a); 
b = cast(0,'like',T.b);
Generated C Code
int adder(short a, short b) 
{ 
  int y; 
  int i0; 
  int i1; 
  int i2; 
  int i3; 
  i0 = a; 
  i1 = b; 
  if ((i0 & 65536) != 0) { 
    i2 = i0 | -65536; 
  } else { 
    i2 = i0 & 65535; 
  } 

  if ((i1 & 65536) != 0) { 
    i3 = i1 | -65536; 
  } else { 
    i3 = i1 & 65535; 
  } 

  i0 = i2 + i3; 
  if ((i0 & 65536) != 0) { 
    y = i0 | -65536; 
  } else { 
    y = i0 & 65535; 
  } 

  return y; 
}

Table 9a. Original MATLAB code and C code generated with default fimath settings.

To make the generated code more efficient, select fixed-point math settings that match your processor’s types. Choose fimath properties for math, rounding, and overflow to define the rules for performing arithmetic operations on your fi objects (Table 9b).

MATLAB Code
Code being compiled: 

function y = adder(a,b) 
  y = a + b; 
end 

With types defined with fimath settings 
that match processor types: 

F = fimath(... 
  'RoundingMethod','Floor', ... 
  'OverflowAction','Wrap', ... 
  'ProductMode','KeepLSB', ... 
  'ProductWordLength',32, ... 
  'SumMode','KeepLSB', ... 
  'SumWordLength',32); 

T.a = fi([],1,16,0,F); 
T.b = fi([],1,16,0,F); 

a = cast(0,'like',T.a); 
b = cast(0,'like',T.b);
Generated C Code
int adder(short a, short b) 
{ 
  return a + b; 
}

Table 9b. Original MATLAB code and C code generated with fimath settings that match processor types.

Replace Built-In Functions with Fixed-Point Implementations

Some MATLAB functions can be replaced to achieve a more efficient fixed-point implementation. For example, you can replace a built-in function with a lookup table implementation or a CORDIC implementation, which only requires iterative shift-add operations.

Re-Implement Division Operations

Division operations are often not fully supported by hardware, and can result in slow processing. When your algorithm requires a division operation, consider replacing it with a faster alternative. If the denominator is power of two, use bit shifting; for example, use bitsra(x,3) instead of x/8. If the denominator is constant, multiply by the inverse; for example, use x*0.2 instead of x/5.

Next Steps

After converting your floating-point code to fixed point by applying these best practices with Fixed-Point Designer, take the time to thoroughly test your fixed-point implementation using a realistic set of test inputs and compare the bit-true simulation results with your floating-point baseline.

Published 2014 - 92226v00

Products Used

Learn More

View Articles for Related Capabilities