rcs
Calculate and plot monostatic and bistatic radar cross section (RCS) of platform, antenna, or array
Syntax
Description
rcs(
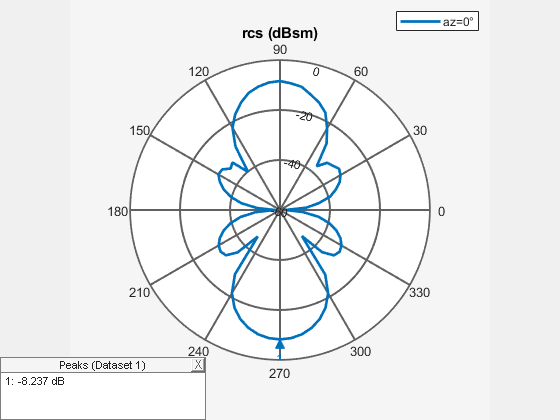
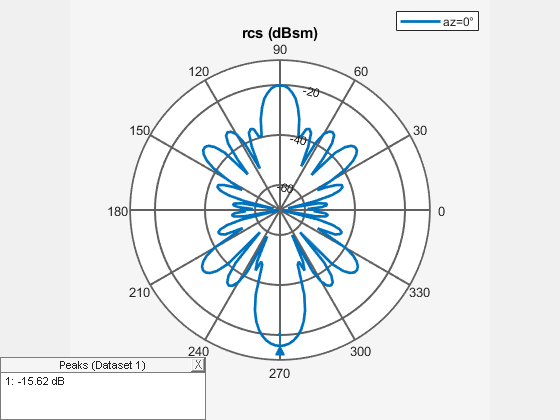
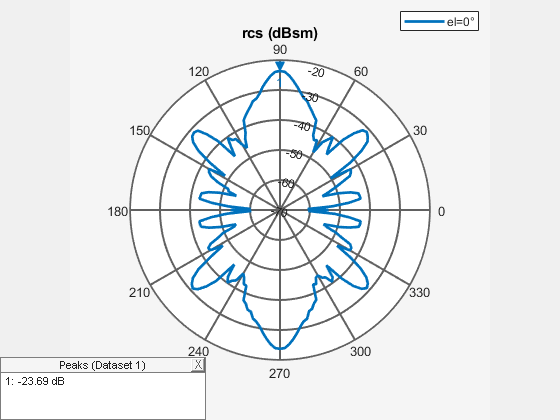
plots the monostatic RCS of the platform, antenna, or array over a specified frequency. To
learn more about monostatic and bistatic RCS, see What Is RCS?.object,frequency)
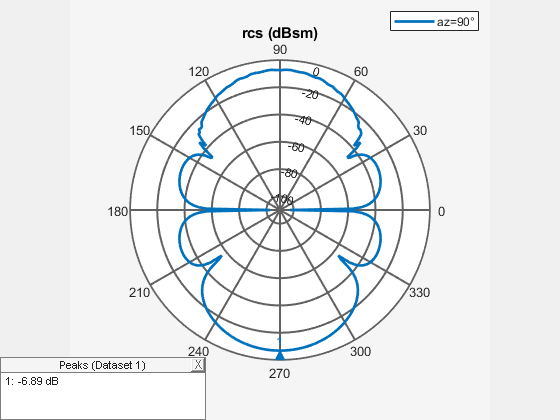
[___] = rcs(___,
specifies additional options using one or more name-value
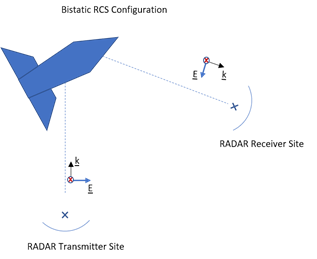
arguments. For a bistatic RCS, specify the TransmitAngle name-value argument
as a 2-by-1 matrix with non-zero values.Name=Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Gurel, L., H. Bagrci, J. C. Castelli, A. Cheraly, F. Tardivel. "Validation Through Comparison: Measurement and Calculation of the Bistatic Radar Cross Section of a Stealth Target." Radio Science. Vol. 38, Number 3, 2003, pp.12-1 - 12-8.
[2] Rao, S.M., D. R. Wilton, A. W. Glisson. "Electromagnetic Scattering by Surfaces of Arbitrary Shape." IEEE Trans. Antennas and Propagation. Vol. AP-30, Number 3, 1982, pp.409-418.
[3] Jakobus, U., F. M. Landstorfer. "Improved PO-MM Formulation for Scattering from Three-Dimensional Perfectly Conducting Bodies of Arbitrary Shape.." IEEE Trans. Antennas and Propagation. Vol. AP-43, Number 2, 1995, pp.162-169.