Flux-Based PMSM

Flux-based permanent magnet synchronous motor

Libraries:
Powertrain Blockset / Propulsion / Electric Motors and Inverters

Description

The Flux-Based PMSM block implements a flux-based three-phase permanent magnet synchronous motor (PMSM) with a tabular-based electromotive force. The block uses the three-phase input voltages to regulate the individual phase currents, allowing control of the motor torque or speed.

Flux-based motor models take into account magnetic saturation and iron losses. To calculate the magnetic saturation and iron loss, the Flux-Based PMSM block uses the inverse of the flux linkages. To obtain the block parameters, you can use finite-element analysis (FEA) or measure phase voltages using a dynamometer.

By default, the block sets the Simulation Type parameter to Continuous to use a continuous sample time during simulation. If you want to generate code for fixed-step double- and single-precision targets, considering setting the parameter to Discrete. Then specify a Sample Time, Ts parameter.

To enable power loss calculations suitable for code generation targets that limit memory, select Enable memory optimized 2D LUT.

Three-Phase Sinusoidal Model Electrical System

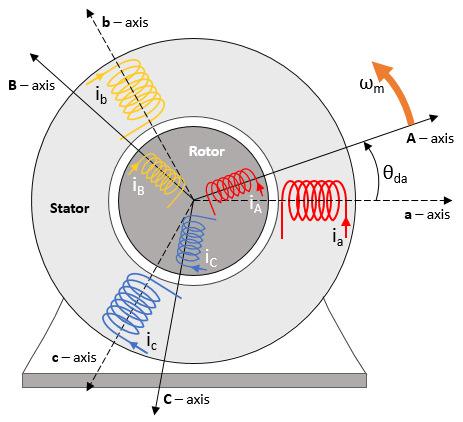
The block implements equations that are expressed in a stationary rotor reference (dq) frame. The d-axis aligns with the a-axis. All quantities in the rotor reference frame are referred to the stator.

The block uses these equations.

Calculation	Equation
q- and d-axis voltage	$\begin{array}{l} v_{d} = \frac{d ψ_{d}}{d t} + R_{s} i_{d} - ω_{e} ψ_{q} \\ v_{q} = \frac{d ψ_{q}}{d t} + R_{s} i_{q} + ω_{e} ψ_{d} \end{array}$
q- and d-axis current	$\begin{array}{l} i_{d} = f (ψ_{d}, ψ_{q}) \\ i_{q} = g (ψ_{d}, ψ_{q}) \end{array}$
Electromechanical torque	$T_{e} = 1.5 P [ψ_{d} i_{q} - ψ_{q} i_{d}]$

The equations use these variables.

ω_m	Rotor mechanical speed
ω_e	Rotor electrical speed
Θ_da	dq stator electrical angle with respect to the rotor a-axis
R_s, R_r	Resistance of the stator and rotor windings, respectively
i_q, i_d	q- and d-axis current, respectively
v_q, v_d	q- and d-axis voltage, respectively
Ψ_q, Ψ_d	q- and d-axis magnet flux, respectively
P	Number of pole pairs
T_e	Electromagnetic torque

Transforms

To calculate the voltages and currents in balanced three-phase (a, b) quantities, quadrature two-phase (α, β) quantities, and rotating (d, q) reference frames, the block uses the Clarke and Park Transforms.

In the transform equations.

$\begin{array}{l} ω_{e} = P ω_{m} \\ \frac{d θ_{e}}{d t} = ω_{e} \end{array}$

Transform	Description	Equations
Clarke	Converts balanced three-phase quantities (a, b) into balanced two-phase quadrature quantities (α, β).	$\begin{array}{l} x_{α} = \frac{2}{3} x_{a} - \frac{1}{3} x_{b} - \frac{1}{3} x_{c} \\ x_{β} = \frac{\sqrt{3}}{2} x_{b} - \frac{\sqrt{3}}{2} x_{c} \end{array}$
Park	Converts balanced two-phase orthogonal stationary quantities (α, β) into an orthogonal rotating reference frame (d, q).	$\begin{array}{l} x_{d} = x_{α} \cos θ_{e} + x_{β} \sin θ_{e} \\ x_{q} = - x_{α} \sin θ_{e} + x_{β} \cos θ_{e} \end{array}$
Inverse Clarke	Converts balanced two-phase quadrature quantities (α, β) into balanced three-phase quantities (a, b).	$\begin{array}{l} x_{a} = x_{a} \\ x_{b} = - \frac{1}{2} x_{α} + \frac{\sqrt{3}}{2} x_{β} \\ x_{c} = - \frac{1}{2} x_{α} - \frac{\sqrt{3}}{2} x_{β} \end{array}$
Inverse Park	Converts an orthogonal rotating reference frame (d, q) into balanced two-phase orthogonal stationary quantities (α, β).	$\begin{array}{l} x_{α} = x_{d} \cos θ_{e} - x_{q} \sin θ_{e} \\ x_{β} = x_{d} \sin θ_{e} + x_{q} \cos θ_{e} \end{array}$

The transforms use these variables.

ω_m	Rotor mechanical speed
P	Motor pole pairs
ω_e	Rotor electrical speed
Θ_e	Rotor electrical angle
x	Phase current or voltage

Mechanical System

The rotor angular velocity is given by:

$\begin{matrix} \frac{d}{d t} ω_{m} = \frac{1}{J} (T_{e} - T_{f} - F ω_{m} - T_{m}) \\ \frac{d θ_{m}}{d t} = ω_{m} \end{matrix}$

The equations use these variables.

J	Combined inertia of rotor and load
F	Combined viscous friction of rotor and load
θ_m	Rotor mechanical angular position
T_m	Rotor shaft torque
T_e	Electromagnetic torque
T_f	Combined rotor and load friction torque
ω_m	Rotor mechanical speed

Power Accounting

For the power accounting, the block implements these equations.

Bus Signal			Description	Variable	Equations
`PwrInfo`	`PwrTrnsfrd` — Power transferred between blocks Positive signals indicate flow into block Negative signals indicate flow out of block	`PwrMtr`	Mechanical power	P_mot	$P_{m o t} = - ω_{m} T_{e}$
		`PwrBus`	Electrical power	P_bus	$P_{b u s} = v_{a n} i_{a} + v_{b n} i_{b} + v_{c n} i_{c}$
	`PwrNotTrnsfrd` — Power crossing the block boundary, but not transferred Positive signals indicate an input Negative signals indicate a loss	`PwrElecLoss`	Resistive power loss	P_elec	$P_{e l e c} = - \frac{3}{2} (R_{s} i_{s d}^{2} + R_{s} i_{s q}^{2})$
		`PwrMechLoss`	Mechanical power loss	P_mech	When Port Configuration is set to `Torque`: $P_{m e c h} = - (ω_{m}^{2} F + \| ω_{m} \| T_{f})$ When Port Configuration is set to `Speed`: $P_{m e c h} = 0$
	`PwrStored` — Stored energy rate of change Positive signals indicate an increase Negative signals indicate a decrease	`PwrMtrStored`	Stored motor power	P_str	$P_{s t r} = P_{b u s} + P_{m o t} + P_{e l e c} + P_{m e c h}$

The equations use these variables.

R_s	Stator resistance
i_a, i_b, i_c	Stator phase a, b, and c current
i_sq, i_sd	Stator q- and d-axis currents
v_an, v_bn, v_cn	Stator phase a, b, and c voltage
ω_m	Angular mechanical velocity of the rotor
F	Combined motor and load viscous damping
T_e	Electromagnetic torque
T_f	Combined motor and load friction torque

Lookup Table Memory Optimization

The data for the Corresponding d-axis current, id and Corresponding q-axis current, iq lookup tables are functions of the d- and q-axis flux.

To enable current calculations suitable for code generation targets that limit memory, select Enable memory optimized 2D LUT. The block uses linear interpolation to optimize the current lookup table values for code generation. This table summarizes the optimization implementation.

Use Case		Implementation
d- and q-axis flux aligns with the lookup table breakpoint values.		Memory-optimized current is current lookup table value at intersection of flux values.
d- and q-axis flux does not align with the lookup table breakpoint values, but is within range.		Memory-optimized current is linear interpolation between corresponding flux values.
d- and q-axis flux does not align with the lookup table breakpoint values, and is out of range.		Cannot compute an memory-optimized current. Block uses extrapolated data.

Extrapolation

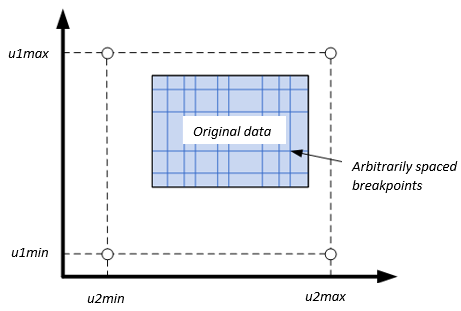
The lookup tables optimized for code generation do not support extrapolation for data that is out of range. However, you can include pre-calculated extrapolation values in the power loss lookup table by selecting Specify Extrapolation.

The block uses the endpoint parameters to resize the table data.

User Input	Extrapolation

Ports

Input

expand all

LdTrq — Rotor shaft torque
`scalar`

Rotor shaft input torque, T_m, in N·m.

Dependencies

To create this port, select Torque for the Port Configuration parameter.

Spd — Rotor shaft speed
`scalar`

Angular velocity of the rotor, ω_m, in rad/s.

Dependencies

To create this port, select Speed for the Port Configuration parameter.

PhaseVolt — Stator terminal voltages
`1`-by-`3` array

Stator terminal voltages, V_a, V_b, and V_c, in V.

Dependencies

To create this port, select Speed or Torque for the Port Configuration parameter.

Output

expand all

Info — Bus signal
bus

The bus signal contains these block calculations.

Signal			Description	Variable	Units
`IaStator`			Stator phase current A	i_a	A
`IbStator`			Stator phase current B	i_b	A
`IcStator`			Stator phase current C	i_c	A
`IdSync`			Direct axis current	i_d	A
`IqSync`			Quadrature axis current	i_q	A
`VdSync`			Direct axis voltage	v_d	V
`VqSync`			Quadrature axis voltage	v_q	V
`MtrSpd`			Angular mechanical velocity of the rotor	ω_m	rad/s
`MtrPos`			Rotor mechanical angular position	θ_m	rad
`MtrTrq`			Electromagnetic torque	T_e	N·m
`PwrInfo`	`PwrTrnsfrd`	`PwrMtr`	Mechanical power	P_mot	W
	`PwrTrnsfrd`	`PwrBus`	Electrical power	P_bus	W
	`PwrNotTrnsfrd`	`PwrElecLoss`	Resistive power loss	P_elec	W
	`PwrNotTrnsfrd`	`PwrMechLoss`	Mechanical power loss	P_mech	W
	`PwrStored`	`PwrMtrStored`	Stored motor power	P_str	W

PhaseCurr — Phase a, b, c current
`1`-by-`3` array

Phase a, b, c current, i_a, i_b, and i_c, in A.

MtrTrq — Motor torque
`scalar`

Motor torque, T_mtr, in N·m.

Dependencies

To create this port, select Speed for the Port configuration parameter.

MtrSpd — Motor speed
`scalar`

Angular speed of the motor, ω_mtr, in rad/s.

Dependencies

To create this port, select Torque for the Port configuration parameter.

Parameters

expand all

Block Options

Simulation type — Select simulation type
`Continuous` (default) | `Discrete`

By default, the block uses a continuous sample time during simulation. If you want to generate code for single-precision targets, considering setting the parameter to Discrete.

Dependencies

Setting Simulation Type to Discrete creates the Sample Time, Ts parameter.

Sample time, Ts — Sample time for discrete integration
`0.001` (default) | `scalar`

Integration sample time for discrete simulation, in s.

Dependencies

Setting Simulation Type to Discrete creates the Sample Time, Ts parameter.

Port Configuration — Select port configuration
`Torque` (default) | `Speed`

This table summarizes the port configurations.

Port Configuration	Creates Input Port	Creates Output Port
`Torque`	`LdTrq`	`MtrSpd`
`Speed`	`Spd`	`MtrTrq`

Enable memory optimized 2D LUT — Selection
`off` (default) | `on`

Enable generation of optimized lookup tables, suitable code generation targets that limit memory.

Vector of d-axis flux, flux_d — Flux breakpoints
`1`-by-`M` vector

d-axis flux, Ψ_d, breakpoints, in Wb.

Resample storage size for flux_d, n1 — Flux bit size
`2` (default) | `4` | `8` | `16` | `32` | `64` | `128` | `256`

Flux breakpoint storage size, n1, dimensionless. The block resamples the Corresponding d-axis current, id and Corresponding q-axis current, iq data based on the storage size.

Dependencies

To create this parameter, select Enable memory optimized 2D LUT.

Vector of q-axis flux, flux_q — Flux breakpoints
`1`-by-`N` vector

q-axis flux, Ψ_q, breakpoints, in Wb.

Resample storage size for flux_q, n2 — Flux bit size
`2` (default) | `4` | `8` | `16` | `32` | `64` | `128` | `256`

Flux breakpoint storage size, n2, dimensionless. The block resamples the Corresponding d-axis current, id and Corresponding q-axis current, iq data based on the storage size.

Dependencies

To create this parameter, select Enable memory optimized 2D LUT.

Corresponding d-axis current, id — 2D lookup table
`M`-by-`N` array

Array of values for d-axis current, i_d, as a function of M d-fluxes, Ψ_d, and N q-fluxes, Ψ_q, in A. Each value specifies the current for a specific combination of d- and q-axis flux. The array size must match the dimensions defined by the flux vectors.

If you set Enable memory optimized 2D LUT, the block converts the data to single precision.

Corresponding q-axis current, iq — 2D lookup table
`M`-by-`N` array

Array of values for q-axis current, i_d, as a function of M d-fluxes, Ψ_d, and N q-fluxes, Ψ_q, in A. Each value specifies the current for a specific combination of d- and q-axis flux. The array size must match the dimensions defined by the flux vectors.

If you set Enable memory optimized 2D LUT, the block converts the data to single precision.

flux_d max endpoint, u1max — Flux breakpoint
`0.22457` (default) | `scalar`

Flux breakpoint maximum extrapolation endpoint, u1max, in Wb.

Dependencies

To create this parameter, select Enable memory optimized 2D LUT and Specify Extrapolation.

flux_d min endpoint, u1min — Flux breakpoint
`-0.22607` (default) | `scalar`

Flux breakpoint minimum extrapolation endpoint, u1min, in Wb.

Dependencies

To create this parameter, select Enable memory optimized 2D LUT and Specify Extrapolation.

flux_q max endpoint, u2max — Flux breakpoint
`0.42959` (default) | `scalar`

Flux breakpoint maximum extrapolation endpoint, u2max, in Wb.

Dependencies

To create this parameter, select Enable memory optimized 2D LUT and Specify Extrapolation.

flux_q min endpoint, u2min — Flux breakpoint
`-0.4296` (default) | `scalar`

Flux breakpoint minimum extrapolation endpoint, u2min, in Wb.

Dependencies

To create this parameter, select Enable memory optimized 2D LUT and Specify Extrapolation.

Stator phase resistance, Rs — Resistance
`0.02` (default) | `scalar`

Stator phase resistance, R_s, in ohm.

Number of pole pairs, P — Pole pairs
`4` (default) | `scalar`

Motor pole pairs, P.

Initial flux, fluxdq0 — Flux
`[0 0]` (default) | `vector`

Initial d- and q-axis flux, Ψ_q0 and Ψ_d0, in Wb.

Initial mechanical position, theta_init — Angle
`0` (default) | `scalar`

Initial rotor angular position, θ_m0, in rad.

Initial mechanical speed, omega_init — Speed
`0` (default) | `scalar`

Initial angular velocity of the rotor, ω_m0, in rad/s.

Dependencies

To enable this parameter, select the Torque configuration parameter.

Physical inertia, viscous damping, and static friction, mechanical — Inertia, damping, friction
`[0.0027, 4.924e-4, 0]` (default) | `vector`

Mechanical properties of the rotor:

Inertia, J, in kgm^2
Viscous damping, F, in N·m/(rad/s)
Static friction, T_f, in N·m

Dependencies

To enable this parameter, select the Torque configuration parameter.

References

[1] Hu, Dakai, Yazan Alsmadi, and Longya Xu. “High-Fidelity Nonlinear IPM Modeling Based on Measured Stator Winding Flux Linkage.” IEEE^® Transactions on Industry Applications 51, no. 4 (July/August 2015).

[2] Chen, Xiao, Jiabin Wang, Bhaskar Sen, Panagiotis Lasari, and Tianfu Sun. “A High-Fidelity and Computationally Efficient Model for Interior Permanent-Magnet Machines Considering the Magnetic Saturation, Spatial Harmonics, and Iron Loss Effect.” IEEE Transactions on Industrial Electronics 62, no. 7 (July 2015).

[3] Ottosson, J., and M. Alakula. “A Compact Field Awakening Controller Implementation.” International Symposium on Power Electronics, Electrical Drives, Automation and Motion, July 2006.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2017b

Flux-Based PMSM

Description

Three-Phase Sinusoidal Model Electrical System

Transforms

Mechanical System

Power Accounting

Lookup Table Memory Optimization

Ports

Input

LdTrq — Rotor shaft torque scalar

Dependencies

Spd — Rotor shaft speed scalar

Dependencies

PhaseVolt — Stator terminal voltages 1-by-3 array

Dependencies

Output

Info — Bus signal bus

PhaseCurr — Phase a, b, c current 1-by-3 array

MtrTrq — Motor torque scalar

Dependencies

MtrSpd — Motor speed scalar

Dependencies

Parameters

Simulation type — Select simulation type Continuous (default) | Discrete

Dependencies

Sample time, Ts — Sample time for discrete integration 0.001 (default) | scalar

Dependencies

Port Configuration — Select port configuration Torque (default) | Speed

Enable memory optimized 2D LUT — Selection off (default) | on

Vector of d-axis flux, flux_d — Flux breakpoints 1-by-M vector

Resample storage size for flux_d, n1 — Flux bit size 2 (default) | 4 | 8 | 16 | 32 | 64 | 128 | 256

Dependencies

Vector of q-axis flux, flux_q — Flux breakpoints 1-by-N vector

Resample storage size for flux_q, n2 — Flux bit size 2 (default) | 4 | 8 | 16 | 32 | 64 | 128 | 256

Dependencies

Corresponding d-axis current, id — 2D lookup table M-by-N array

Corresponding q-axis current, iq — 2D lookup table M-by-N array

flux_d max endpoint, u1max — Flux breakpoint 0.22457 (default) | scalar

Dependencies

flux_d min endpoint, u1min — Flux breakpoint -0.22607 (default) | scalar

Dependencies

flux_q max endpoint, u2max — Flux breakpoint 0.42959 (default) | scalar

Dependencies

flux_q min endpoint, u2min — Flux breakpoint -0.4296 (default) | scalar

Dependencies

Stator phase resistance, Rs — Resistance 0.02 (default) | scalar

Number of pole pairs, P — Pole pairs 4 (default) | scalar

Initial flux, fluxdq0 — Flux [0 0] (default) | vector

Initial mechanical position, theta_init — Angle 0 (default) | scalar

Initial mechanical speed, omega_init — Speed 0 (default) | scalar

Dependencies

Physical inertia, viscous damping, and static friction, mechanical — Inertia, damping, friction [0.0027, 4.924e-4, 0] (default) | vector

Dependencies

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Topics

LdTrq — Rotor shaft torque
`scalar`

Spd — Rotor shaft speed
`scalar`

PhaseVolt — Stator terminal voltages
`1`-by-`3` array

Info — Bus signal
bus

PhaseCurr — Phase a, b, c current
`1`-by-`3` array

MtrTrq — Motor torque
`scalar`

MtrSpd — Motor speed
`scalar`

Simulation type — Select simulation type
`Continuous` (default) | `Discrete`

Sample time, Ts — Sample time for discrete integration
`0.001` (default) | `scalar`

Port Configuration — Select port configuration
`Torque` (default) | `Speed`

Enable memory optimized 2D LUT — Selection
`off` (default) | `on`

Vector of d-axis flux, flux_d — Flux breakpoints
`1`-by-`M` vector

Resample storage size for flux_d, n1 — Flux bit size
`2` (default) | `4` | `8` | `16` | `32` | `64` | `128` | `256`

Vector of q-axis flux, flux_q — Flux breakpoints
`1`-by-`N` vector

Resample storage size for flux_q, n2 — Flux bit size
`2` (default) | `4` | `8` | `16` | `32` | `64` | `128` | `256`

Corresponding d-axis current, id — 2D lookup table
`M`-by-`N` array

Corresponding q-axis current, iq — 2D lookup table
`M`-by-`N` array

flux_d max endpoint, u1max — Flux breakpoint
`0.22457` (default) | `scalar`

flux_d min endpoint, u1min — Flux breakpoint
`-0.22607` (default) | `scalar`

flux_q max endpoint, u2max — Flux breakpoint
`0.42959` (default) | `scalar`

flux_q min endpoint, u2min — Flux breakpoint
`-0.4296` (default) | `scalar`

Stator phase resistance, Rs — Resistance
`0.02` (default) | `scalar`

Number of pole pairs, P — Pole pairs
`4` (default) | `scalar`

Initial flux, fluxdq0 — Flux
`[0 0]` (default) | `vector`

Initial mechanical position, theta_init — Angle
`0` (default) | `scalar`

Initial mechanical speed, omega_init — Speed
`0` (default) | `scalar`

Physical inertia, viscous damping, and static friction, mechanical — Inertia, damping, friction
`[0.0027, 4.924e-4, 0]` (default) | `vector`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.