Processor-In-The-Loop Execution with the GPU Coder App
Use the processor-in-the-loop (PIL) execution to check the numerical behavior of the CUDA® code that you generate from MATLAB® functions. A PIL simulation, which requires target connectivity, compiles generated source code, and then downloads and runs object code on NVIDIA® GPU platforms. The results of the PIL simulation are transferred to MATLAB to verify the numerical equivalence of the simulation and the code generation results.
The PIL verification process is a crucial part of the design cycle to check that the behavior of the generated code matches the design. PIL verification requires an Embedded Coder® license.
Note
When using PIL execution, make sure that the Benchmarking option in
GPU Coder™ settings is false. Executing PIL with benchmarking results
in compilation errors.
Note
GPU Coder does not support collecting code coverage metrics during software-in-the-loop (SIL) and processor-in-the-loop (PIL) simulations.
Prerequisites
Target Board Requirements
NVIDIA DRIVE® or Jetson™ embedded platform.
Ethernet crossover cable to connect the target board and host PC (if the target board cannot be connected to a local network).
NVIDIA CUDA toolkit installed on the board.
Environment variables on the target for the compilers and libraries. For information on the supported versions of the compilers and libraries and their setup, see Prerequisites for Generating Code for NVIDIA Boards.
Development Host Requirements
GPU Coder for CUDA code generation. For help on getting started with GPU Coder, see Get Started with GPU Coder (GPU Coder).
NVIDIA CUDA toolkit on the host.
Environment variables on the host for the compilers and libraries. For information on the supported versions of the compilers and libraries, see Third-Party Hardware (GPU Coder). For setting up the environment variables, see Set Environment Variables (GPU Coder).
Example: The Mandelbrot Set
Description
You do not have to be familiar with the algorithm in the example to complete the tutorial.
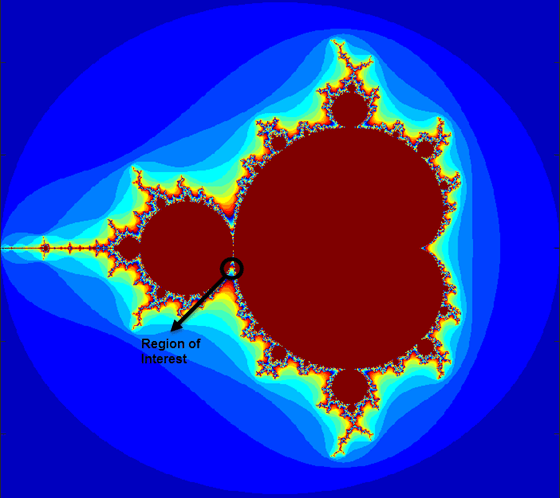
The Mandelbrot set is the region in the complex plane consisting of the values z0 for which the trajectories defined by
remain bounded at k→∞. The overall geometry of the Mandelbrot set is shown in the figure. This view does not have the resolution to show the richly detailed structure of the fringe just outside the boundary of the set. At increasing magnifications, the Mandelbrot set exhibits an elaborate boundary that reveals progressively finer recursive detail.
Algorithm
Create a MATLAB function called mandelbrot_count.m with the following
lines of code. This code is a baseline vectorized MATLAB implementation of the Mandelbrot
set.
function count = mandelbrot_count(maxIterations, xGrid, yGrid) %#codegen % mandelbrot computation z0 = complex(xGrid,yGrid); count = ones(size(z0)); % Add Kernelfun pragma to trigger kernel creation coder.gpu.kernelfun; z = z0; for n = 0:maxIterations z = z.*z + z0; inside = abs(z)<=2; count = count + inside; end count = log(count);
For this tutorial, pick a set of limits that specify a highly zoomed part of the Mandelbrot set in the valley between the main cardioid and the p/q bulb to its left. A 1000x1000 grid of real parts (x) and imaginary parts (y) is created between these two limits. The Mandelbrot algorithm is then iterated at each grid location. An iteration number of 500 is enough to render the image in full resolution.
Create a MATLAB script called mandelbrot_test.m with the following lines
of code. It also calls the mandelbrot_count function and plots the
resulting Mandelbrot set.
maxIterations = 500; gridSize = 1000; xlim = [-0.748766713922161, -0.748766707771757]; ylim = [ 0.123640844894862, 0.123640851045266]; x = linspace( xlim(1), xlim(2), gridSize ); y = linspace( ylim(1), ylim(2), gridSize ); [xGrid,yGrid] = meshgrid( x, y ); count = mandelbrot_count(maxIterations, xGrid, yGrid); figure(1) imagesc( x, y, count ); colormap([jet();flipud( jet() );0 0 0]); axis off title('Mandelbrot set');
GPU Coder App
To open the GPU Coder app, on the MATLAB toolstrip, in the Apps tab, under Code
Generation, click the GPU Coder app icon. You can also open the app by typing gpucoder (GPU Coder) in
the MATLAB Command Window.
The app opens the Create GPU Coder Project dialog box. Enter a name for the GPU Coder project. The GPU Coder app opens a GPU Coder tab and a GPU Coder panel.
In the GPU Coder panel, select Add Entry Points. In the Entry Points tab, specify the entry-point function as
mandelbrot_count.In the Automatically Define Input Types list, select
Using Command Window. Press Start, and enter this code in the MATLAB Command Window.Press Stop.mandelbrot_count(500,zeros(1000),zeros(1000));
In the toolstrip, set the Output Type to Static Library.
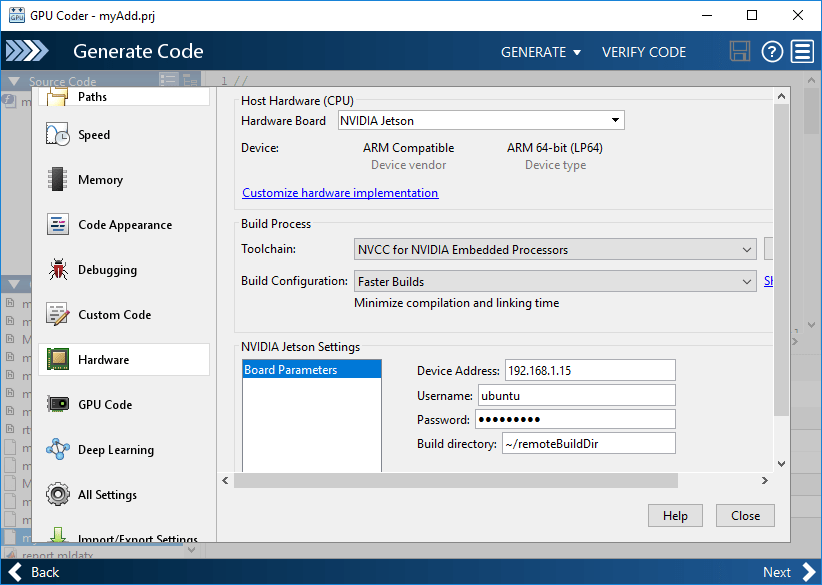
In the toolstrip, click Settings. In the left pane, open the Hardware settings. In the right pane, set Hardware board to
NVIDIA Jetson.Click Configure Hardware. In the dialog box, enter the board address, username, and password.
In the GPU Coder tab, select Run Using PIL > Select MATLAB file to run. Select the
mandelbrot_testscript.The GPU Coder app:
Generates a standalone library, for example,
codegen\lib\mandelbrot_count.Generates PIL interface code, for example,
codegen\lib\mandelbrot_count\pil.Runs the test file, replacing calls to the MATLAB function with calls to the generated code in the library.
Displays messages from the PIL execution in the MATLAB Command Window and the Output section of the GPU Coder panel.
Note
On a Microsoft® Windows® system, the Windows Firewall can potentially block a PIL execution. Change the Windows Firewall settings to allow access.
Verify that the results from the PIL execution match the results from the original MATLAB functions.
To terminate the PIL execution process, click Stop PIL Verification. Alternatively, on the MATLAB Command Window, click the link that follows To terminate execution.
==== Verifying using SIL/PIL ==== ### Connectivity configuration for function 'mandelbrot_count': 'NVIDIA Jetson' PIL execution is using Port 17725. PIL execution is using 30 Sec(s) for receive time-out. Code generation successful: View report ### Starting application: 'codegen\lib\mandelbrot_count\pil\mandelbrot_count.elf' To terminate execution: clear mandelbrot_count_pil ### Launching application mandelbrot_count.elf...
See Also
Functions
jetson|drive|webcam|getPILPort|getPILTimeout|setPILPort|setPILTimeout
Objects
Topics
- Sobel Edge Detection on NVIDIA Jetson Nano Using Raspberry Pi Camera Module V2
- Processor-in-the-Loop Execution on NVIDIA Targets Using GPU Coder
- Build and Run an Executable on NVIDIA Hardware
- Stop or Restart an Executable Running on NVIDIA Hardware
- Run Linux Commands on NVIDIA Hardware
- Processor-in-the-Loop Execution from Command Line
- Execution-Time Profiling for PIL