使用 Parallel Computing Toolbox 加速 BER 仿真

此示例使用:

打开脚本

此示例使用 Parallel Computing Toolbox™ 加速一个简单的 QPSK 误码率 (BER) 仿真。该系统由 QPSK 调制器、QPSK 解调器、AWGN 信道和误码率计数器组成。

设置仿真参数。

EbNoVec = 5:8;     % Eb/No values in dB
totalErrors = 200; % Number of bit errors needed for each Eb/No value
totalBits = 1e7;   % Total number of bits transmitted for each Eb/No value

为用于存储由 helper_qpsk_sim_with_awgn 函数生成的数据的数组分配内存。

[numErrors, numBits] = deal(zeros(length(EbNoVec),1));

运行仿真并确定执行时间。这里将仅使用一个处理器来确定基线性能。因此，我们可以看到，采用的是常规的 for 循环。

tic
for idx = 1:length(EbNoVec)
    errorStats = helper_qpsk_sim_with_awgn(EbNoVec,idx, ...
        totalErrors,totalBits);
    numErrors(idx) = errorStats(idx,2);
    numBits(idx) = errorStats(idx,3);
end
simBaselineTime = toc;

计算 BER。

ber1 = numErrors ./ numBits;

在 Parallel Computing Toolbox 可用的情况下重新运行仿真。创建一个工作单元池。

pool = gcp;
assert(~isempty(pool), ['Cannot create parallel pool. '...
    'Try creating the pool manually using ''parpool'' command.'])

Starting parallel pool (parpool) using the 'Processes' profile ...
17-Jan-2025 15:54:13: Job Queued. Waiting for parallel pool job with ID 1 to start ...
Connected to parallel pool with 6 workers.

从 pool 的 NumWorkers 属性确定可用工作单元的数量。仿真在每个工作单元上运行 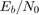$E_{b}/N_{0}$ 值的范围，而不是将单个 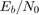$E_{b}/N_{0}$ 点分配给每个工作单元，因为前一种方法能实现最大的性能提升。

numWorkers = pool.NumWorkers;

确定用于嵌套 parfor 循环的 EbNoVec 的长度。为了正确进行变量分类，嵌套在 parfor 中的 for 循环的范围必须由常数或变量定义。

lenEbNoVec = length(EbNoVec);

为用于存储由 helper_qpsk_sim_with_awgn 函数生成的数据的数组分配内存。

[numErrors,numBits] = deal(zeros(length(EbNoVec),numWorkers));

运行仿真并确定执行时间。

tic
parfor n = 1:numWorkers
    for idx = 1:lenEbNoVec
        errorStats = helper_qpsk_sim_with_awgn(EbNoVec,idx, ...
            totalErrors/numWorkers,totalBits/numWorkers);
        numErrors(idx,n) = errorStats(idx,2);
        numBits(idx,n) = errorStats(idx,3);
    end
end
simParallelTime = toc;

计算 BER。在这种情况下，必须合并多个处理器的结果以生成聚合 BER。

ber2 = sum(numErrors,2) ./ sum(numBits,2);

比较 BER 值，以验证无论工作单元数量如何都能获得相同的结果。

semilogy(EbNoVec',ber1,'-*',EbNoVec',ber2,'-^')
legend('Single Processor','Multiple Processors','location','best')
xlabel('Eb/No (dB)')
ylabel('BER')
grid

您可以看到，BER 曲线本质上相同，任何差异均由随机数种子不同引起。

比较每种方法的执行时间。

fprintf(['\nSimulation time = %4.1f sec for one worker\n', ...
    'Simulation time = %4.1f sec for multiple workers\n'], ...
    simBaselineTime,simParallelTime)
fprintf('Number of processors for parfor = %d\n', numWorkers)

Simulation time = 313.8 sec for one worker
Simulation time = 78.1 sec for multiple workers
Number of processors for parfor = 6

另请参阅

| (Parallel Computing Toolbox)

主题