Decision Feedback Equalizer

Equalize modulated signals using decision feedback filtering

Libraries:
Communications Toolbox / Equalizers

Description

The Decision Feedback Equalizer block uses a decision feedback filter tap delay line with a weighted sum to equalize modulated signals transmitted through a dispersive channel. Using an estimate of the channel modeled as a finite input response (FIR) filter, the block processes input frames and outputs the estimated signal.

This icon shows the block with all ports enabled for configurations that use the LMS or RLS adaptive algorithm.

This icon shows the block with all ports enabled for configurations that use the CMA adaptive algorithm.

Examples

expand all

DF Equalize QPSK-Modulated Signal in Simulink

This example uses:

Open Model

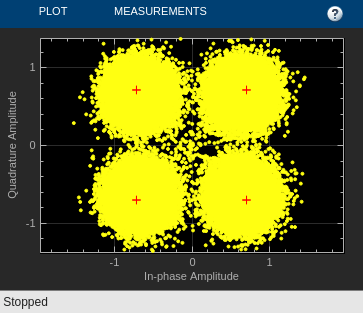
Apply decision feedback equalization using the least mean squares (LMS) algorithm to recover QPSK symbols passed through an AWGN channel.

The slex_dfeq_qpsk_signal model generates an M=4 sequence using the Random Integer Generator block. The sequence is modulated with the M-PSK Modulator Baseband block, filtered with the Discrete FIR Filter block, and then impaired with the AWGN block. The Decision Feedback Equalizer block equalizes the data sequence, the data is demodulated with the M-PSK Demodulator Baseband block, and the bit error rate is computed. The signal path out of the modulator is split to a Selector block, which provides the first 1000 symbols of the modulated signal to the equalizer as an initial training sequence.

No delay is introduced between the transmitted and received signal because the maximum tap value is the first tap of the discrete FIR filter and the equalizer reference tap is 1. The equalizer converges after around 1000 symbols so this value is used for the computation delay of the Error Rate Calculation block.

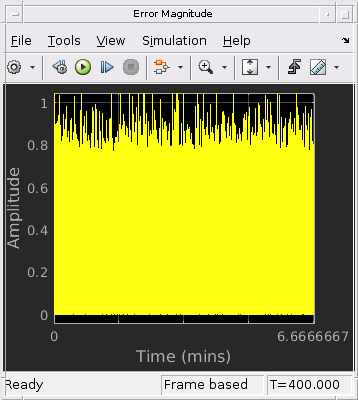
The computed error rate is displayed and plots show the equalized constellation, equalized tap weights, and signal error magnitude.

Computed error rate = 0.00077778

Extended Examples

Adaptive Equalization with Filtering and Fading Channel

The behavior of the selected adaptive equalizer in a communication link that has a fading channel. The transmitter and receiver have root raised cosine pulse shaped filtering. A subsystem block enables you to select between linear or decision feedback equalizers that use the least mean square (LMS) or recursive least square (RLS) adaptive algorithm.

Open Model

Ports

Input

expand all

in — Input signal
column vector

Input signal, specified as a column vector. The vector length of in must be equal to an integer multiple of the Number of input samples per symbol parameter. For more information, see Symbol Tap Spacing.

Data Types: double
Complex Number Support: Yes

Desired — Training symbols
column vector

Training symbols, specified as a column vector. The vector length of Desired must be less than or equal to the length of input in. The Desired input port is ignored when the Train input port is 0.

Dependencies

To enable this port, set the Adaptive algorithm parameter to LMS or RLS.

Data Types: double
Complex Number Support: Yes

Train — Train equalizer flag
boolean scalar

Train equalizer flag, specified as 1 or 0. The block starts training when this value changes from 0 to 1 (at the rising edge). The block trains until all symbols in the Desired input port are processed.

Dependencies

To enable this port, set the Adaptive algorithm parameter to LMS or RLS and select the Enable training control input parameter.

Data Types: Boolean

Update — Update tap weights flag
`1` | `0`

Update tap weights flag, specified as 1 or 0. The tap weights are updated when this value is 1.

Dependencies

To enable this port, set the Adaptive algorithm parameter to CMA and the Source of adapt weights flag parameter to Input port.

Data Types: Boolean

Reset — Reset equalizer flag
`1` | `0`

Reset equalizer flag, specified as 1 or 0. If Reset is set to 1, the block resets the tap weights before processing the incoming signal. The block performs initial training until all symbols in the Desired input port are processed.

Dependencies

To enable this port, select the Enable reset input parameter.

Data Types: Boolean

Output

expand all

Out — Equalized symbols
column vector

Equalized symbols, returned as a column vector that has the same length as input signal in.

This port is unnamed until you select the Output error signal or Output taps weights parameter.

Err — Error signal
column vector

Error signal, returned as a column vector that has the same length as input signal in.

w — Tap weights
column vector

Tap weights, returned as an N_Taps-by-1 vector, where N_Taps is equal to the sum of the Number of forward taps and Number of feedback taps parameter values. w contains the tap weights from the last tap weight update.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Structure parameters

Number of forward taps — Number of forward equalizer taps
`5` (default) | positive integer

Number of forward equalizer taps, specified as a positive integer. The number of forward equalizer taps must be greater than or equal to the value of the Number of input samples per symbol parameter.

Number of feedback taps — Number of feedback equalizer taps
`3` (default) | positive integer

Number of feedback equalizer taps, specified as a positive integer.

Signal constellation — Signal constellation
`pskmod(0:3,4,pi/4)` (default) | vector

Signal constellation, specified as a vector. The default value is a QPSK constellation generated using this code: pskmod(0:3,4,pi/4).

Number of input samples per symbol — Number of input samples per symbol
`1` (default) | positive integer

Number of input samples per symbol, specified as a positive integer. Setting this parameter to any number greater than 1 effectively creates a fractionally spaced equalizer. For more information, see Symbol Tap Spacing.

Algorithm parameters

Adaptive algorithm — Adaptive algorithm
`LMS` (default) | `RLS` | `CMA`

Adaptive algorithm used for equalization, specified as one of these values:

LMS — Update the equalizer tap weights using the Least Mean Square (LMS) Algorithm.
RLS — Update the equalizer tap weights using the Recursive Least Square (RLS) Algorithm.
CMA — Update the equalizer tap weights using the Constant Modulus Algorithm (CMA).

Step size — Step size
`0.01` (default) | positive scalar

Step size used by the adaptive algorithm, specified as a positive scalar. Increasing the step size reduces the equalizer convergence time but causes the equalizer output estimates to be less stable.

Tunable: Yes

Dependencies

To enable this parameter, set Adaptive algorithm to LMS or CMA.

Forgetting factor — Forgetting factor
`0.99` (default) | scalar in the range (0, 1]

Forgetting factor used by the adaptive algorithm, specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the equalizer convergence time but causes the equalizer output estimates to be less stable.

Tunable: Yes

Dependencies

To enable this parameter, set Adaptive algorithm to RLS.

Initial inverse correlation matrix — Initial inverse correlation matrix
`0.1` (default) | scalar | matrix

Initial inverse correlation matrix, specified as a scalar or an N_Taps-by-N_Taps matrix. N_Taps is equal to the sum of the Number of forward taps and Number of feedback taps parameter values. If you specify this value as a scalar, a, the equalizer sets the initial inverse correlation matrix to a times the identity matrix: a(eye(N_Taps)).

Dependencies

To enable this parameter, set Adaptive algorithm to RLS.

Control parameters

Reference tap — Reference tap
`3` (default) | positive integer

Reference tap, specified as a positive integer less than or equal to the Number of forward taps parameter value. The equalizer uses the reference tap location to track the main energy of the channel.

Input signal delay (samples) — Input signal delay
`0` (default) | nonnegative integer

Input signal delay in samples relative to the reset time of the equalizer, specified as a nonnegative integer. If the input signal is a vector of length greater than 1, then the input delay is relative to the start of the input vector. If the input signal is a scalar, then the input delay is relative to the first call of the block and to the first call of the block after the Reset input port toggles to 1.

Dependencies

To enable this parameter, set Adaptive algorithm to LMS or RLS.

Source of adapt weights flag — Source of adapt tap weights request
`Property` (default) | `Input port`

Source of the adapt tap weights request, specified as one of these values:

Property — Specify this value to use the Adaptive algorithm parameter to control when the block adapts tap weights.
Input port — Specify this value to use the Update input port to control when the block adapts tap weights.

Dependencies

To enable this parameter, set Adaptive algorithm to CMA.

Adapt tap weights — Adapt tap weights
`on` (default) | `off`

Select this parameter to adaptively update the equalizer tap weights. If this parameter is cleared, the block keeps the equalizer tap weights unchanged.

Dependencies

To enable this parameter, set Adaptive algorithm to CMA and Source of adapt weights flag to Property.

Initial tap weights source — Source for initial tap weights
`Auto` (default) | `Property`

Source for initial tap weights, specified as one of these values:

Auto — Initialize the tap weights to the algorithm-specific default values, as described in the Initial weights parameter.
Property — Initialize the tap weights using the Initial weights parameter value.

Initial weights — Initial tap weights
`0` or `[0;0;1;0;0]` (default) | scalar | column vector

Initial tap weights used by the adaptive algorithm, specified as a scalar or an N_Taps-by-1 vector. N_Taps is equal to the sum of the Number of forward taps and Number of feedback taps parameter values. The default is 0 when the Adaptive algorithm parameter is set to LMS or RLS. The default is [0;0;1;0;0] when the Adaptive algorithm parameter is set to CMA.

If you specify Initial weights as a vector, the vector length must be N_Taps. If you specify Initial weights as a scalar, the equalizer uses scalar expansion to create a vector of length N_Taps with all values set to Initial weights.

Dependencies

To enable this parameter, set Initial tap weights source to Property.

Tap weight update period (symbols) — Tap weight update period
`1` (default) | positive integer

Tap weight update period in symbols, specified as a positive integer. The equalizer updates the tap weights after processing this number of symbols.

Enable training control input — Enable training control input
`off` (default) | `on`

Select this parameter to enable input port Train. If this parameter is cleared, the block does not reenter training mode after the initial tap training.

Dependencies

To enable this parameter, set Adaptive algorithm to LMS or RLS.

Update tap weights when not training — Update tap weights when not training
`on` (default) | `off`

Select this parameter to use decision directed mode to update equalizer tap weights. If this parameter is cleared, the block keeps the equalizer tap weights unchanged after training.

Dependencies

To enable this parameter, set Adaptive algorithm to LMS or RLS.

Enable reset input — Enable reset input
`off` (default) | `on`

Select this parameter to enable input port Reset. If this parameter is cleared, the block does not reset the tap weights before processing the incoming signal.

Diagnostic parameters

Output error signal — Enable error signal output
`off` (default) | `on`

Select this parameter to enable output port Err containing the equalizer error signal.

Output taps weights — Enable tap weights output
`off` (default) | `on`

Select this parameter to enable output port w containing tap weights from the last tap weight update.

Simulate using — Type of simulation to run
`Code generation` (default) | `Interpreted execution`

Type of simulation to run, specified as Code generation or Interpreted execution.

Code generation — Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with the Interpreted execution option.
Interpreted execution — Simulate the model by using the MATLAB^® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with the Code generation option. In this mode, you can debug the source code of the block.

For more information, see Interpreted Execution vs. Code Generation (Simulink).

Block Characteristics

Data Types	`double` \| `single`
Multidimensional Signals	`no`
Variable-Size Signals	`yes`

More About

expand all

Symbol Tap Spacing

You can configure the equalizer to operate as a symbol-spaced equalizer or as a fractional symbol-spaced equalizer.

To operate the equalizer at a symbol-spaced rate, specify the number of samples per symbol as 1. Symbol-rate equalizers have taps spaced at the symbol duration. Symbol-rate equalizers are sensitive to timing phase.
To operate the equalizer at a fractional symbol-spaced rate, specify the number of input samples per symbol as an integer greater than 1 and provide an input signal oversampled at that sampling rate. Fractional symbol-spaced equalizers have taps spaced at an integer fraction of the input symbol duration. Fractional symbol-spaced equalizers are not sensitive to timing phase.

Algorithms

expand all

Decision Feedback Equalizers

A decision feedback equalizer (DFE) is a nonlinear equalizer that reduces intersymbol interference (ISI) in frequency-selective channels. If a null exists in the frequency response of a channel, DFEs do not enhance the noise. A DFE consists of a tapped delay line that stores samples from the input signal and contains a forward filter and a feedback filter. The forward filter is similar to a linear equalizer. The feedback filter contains a tapped delay line whose inputs are the decisions made on the equalized signal. Once per symbol period, the equalizer outputs a weighted sum of the values in the delay line and updates the weights to prepare for the next symbol period.

DFEs can be symbol-spaced or fractional symbol-spaced.

For a symbol-spaced equalizer, the number of samples per symbol, K, is 1. The output sample rate equals the input sample rate.
For a fractional symbol-spaced equalizer, the number of samples per symbol, K, is an integer greater than 1. Typically, K is 4 for fractional symbol-spaced equalizers. The output sample rate is 1/T and the input sample rate is K/T. Tap weight updating occurs at the output rate.

This schematic shows a fractional symbol-spaced DFE with a total of N weights, a symbol period of T, and K samples per symbol. The filter has L forward weights and N-L feedback weights. The forward filter is at the top, and the feedback filter is at the bottom. If K is 1, the result is a symbol-spaced DFE instead of a fractional symbol-spaced DFE.

In each symbol period, the equalizer receives K input samples at the forward filter and one decision or training sample at the feedback filter. The equalizer then outputs a weighted sum of the values in the forward and feedback delay lines and updates the weights to prepare for the next symbol period.

Note

The algorithm for the Adaptive Algorithm block in the schematic jointly optimizes the forward and feedback weights. Joint optimization is especially important for convergence in the recursive least square (RLS) algorithm.

For more information, see Equalization.

Least Mean Square (LMS) Algorithm

For the LMS algorithm, in the previous schematic, w is a vector of all weights w_i, and u is a vector of all inputs u_i. Based on the current set of weights, the LMS algorithm creates the new set of weights as

w_new = w_current + (StepSize) ue*.

The step size used by the adaptive algorithm is specified as a positive scalar. Increasing the step size reduces the equalizer convergence time but causes the equalized output signal to be less stable. To determine the maximum step size allowed when using the LMS adaptive algorithm, use the maxstep object function. The * operator denotes the complex conjugate and the error calculation e = d - y.

Recursive Least Square (RLS) Algorithm

For the RLS algorithm, in the previous schematic, w is the vector of all weights w_i, and u is the vector of all inputs u_i. Based on the current set of inputs, u, and the inverse correlation matrix, P, the RLS algorithm first computes the Kalman gain vector, K, as

$K = \frac{P u}{(F o r g e t t i n g F a c t o r) + u^{H} P u} .$

The forgetting factor used by the adaptive algorithm is specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the equalizer convergence time but causes the equalized output signal to be less stable. H denotes the Hermitian transpose. Based on the current inverse correlation matrix, the new inverse correlation matrix is

$P_{new} = \frac{(1 - K u^{H}) P_{current}}{F o r g e t t i n g F a c t o r} .$

Based on the current set of weights, the RLS algorithm creates the new set of weights as

w_new = w_current+K*e.

The * operator denotes the complex conjugate and the error calculation e = d - y.

Constant Modulus Algorithm (CMA)

For the CMA adaptive algorithm, in the previous schematic, w is the vector of all weights w_i, and u is the vector of all inputs u_i. Based on the current set of weights, the CMA adaptive algorithm creates the new set of weights as

w_new = w_current + (StepSize) u*e.

The step size used by the adaptive algorithm is specified as a positive scalar. Increasing the step size reduces the equalizer convergence time but causes the equalized output signal to be less stable. To determine the maximum step size allowed by the CMA adaptive algorithm, use the maxstep object function. The * operator denotes the complex conjugate and the error calculation e = y(R - |y|²), where R is a constant related to the signal constellation.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2019a

Decision Feedback Equalizer

Description

Examples

DF Equalize QPSK-Modulated Signal in Simulink

Extended Examples

Adaptive Equalization with Filtering and Fading Channel

Ports

Input

in — Input signal column vector

Desired — Training symbols column vector

Dependencies

Train — Train equalizer flag boolean scalar

Dependencies

Update — Update tap weights flag 1 | 0

Dependencies

Reset — Reset equalizer flag 1 | 0

Dependencies

Output

Out — Equalized symbols column vector

Err — Error signal column vector

w — Tap weights column vector

Parameters

Number of forward taps — Number of forward equalizer taps 5 (default) | positive integer

Number of feedback taps — Number of feedback equalizer taps 3 (default) | positive integer

Signal constellation — Signal constellation pskmod(0:3,4,pi/4) (default) | vector

Number of input samples per symbol — Number of input samples per symbol 1 (default) | positive integer

Adaptive algorithm — Adaptive algorithm LMS (default) | RLS | CMA

Step size — Step size 0.01 (default) | positive scalar

Dependencies

Forgetting factor — Forgetting factor 0.99 (default) | scalar in the range (0, 1]

Dependencies

Initial inverse correlation matrix — Initial inverse correlation matrix 0.1 (default) | scalar | matrix

Dependencies

Reference tap — Reference tap 3 (default) | positive integer

Input signal delay (samples) — Input signal delay 0 (default) | nonnegative integer

Dependencies

Source of adapt weights flag — Source of adapt tap weights request Property (default) | Input port

Dependencies

Adapt tap weights — Adapt tap weights on (default) | off

Dependencies

Initial tap weights source — Source for initial tap weights Auto (default) | Property

Initial weights — Initial tap weights 0 or [0;0;1;0;0] (default) | scalar | column vector

Dependencies

Tap weight update period (symbols) — Tap weight update period 1 (default) | positive integer

Enable training control input — Enable training control input off (default) | on

Dependencies

Update tap weights when not training — Update tap weights when not training on (default) | off

Dependencies

Enable reset input — Enable reset input off (default) | on

Output error signal — Enable error signal output off (default) | on

Output taps weights — Enable tap weights output off (default) | on

Simulate using — Type of simulation to run Code generation (default) | Interpreted execution

Block Characteristics

More About

Symbol Tap Spacing

Algorithms

Decision Feedback Equalizers

Least Mean Square (LMS) Algorithm

Recursive Least Square (RLS) Algorithm

Constant Modulus Algorithm (CMA)

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Blocks

Objects

Topics

in — Input signal
column vector

Desired — Training symbols
column vector

Train — Train equalizer flag
boolean scalar

Update — Update tap weights flag
`1` | `0`

Reset — Reset equalizer flag
`1` | `0`

Out — Equalized symbols
column vector

Err — Error signal
column vector

w — Tap weights
column vector

Number of forward taps — Number of forward equalizer taps
`5` (default) | positive integer

Number of feedback taps — Number of feedback equalizer taps
`3` (default) | positive integer

Signal constellation — Signal constellation
`pskmod(0:3,4,pi/4)` (default) | vector

Number of input samples per symbol — Number of input samples per symbol
`1` (default) | positive integer

Adaptive algorithm — Adaptive algorithm
`LMS` (default) | `RLS` | `CMA`

Step size — Step size
`0.01` (default) | positive scalar

Forgetting factor — Forgetting factor
`0.99` (default) | scalar in the range (0, 1]

Initial inverse correlation matrix — Initial inverse correlation matrix
`0.1` (default) | scalar | matrix

Reference tap — Reference tap
`3` (default) | positive integer

Input signal delay (samples) — Input signal delay
`0` (default) | nonnegative integer

Source of adapt weights flag — Source of adapt tap weights request
`Property` (default) | `Input port`

Adapt tap weights — Adapt tap weights
`on` (default) | `off`

Initial tap weights source — Source for initial tap weights
`Auto` (default) | `Property`

Initial weights — Initial tap weights
`0` or `[0;0;1;0;0]` (default) | scalar | column vector

Tap weight update period (symbols) — Tap weight update period
`1` (default) | positive integer

Enable training control input — Enable training control input
`off` (default) | `on`

Update tap weights when not training — Update tap weights when not training
`on` (default) | `off`

Enable reset input — Enable reset input
`off` (default) | `on`

Output error signal — Enable error signal output
`off` (default) | `on`

Output taps weights — Enable tap weights output
`off` (default) | `on`

Simulate using — Type of simulation to run
`Code generation` (default) | `Interpreted execution`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.