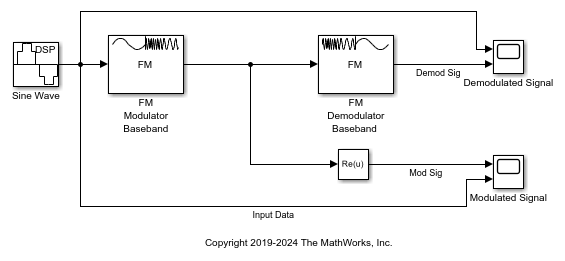
FM Demodulator Baseband
Demodulate using FM method
Libraries:
Communications Toolbox /
Modulation /
Analog Baseband Modulation
Description
The FM Demodulator Baseband block demodulates a complex input signal and returns a real output signal.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
A frequency-modulated passband signal, Y(t), is given as
where:
A is the carrier amplitude.
fc is the carrier frequency.
x(τ) is the baseband input signal.
fΔ is the frequency deviation in Hz.
The frequency deviation is the maximum shift from fc in one direction, assuming |x(τ)| ≤ 1.
A baseband FM signal can be derived from the passband representation by downconverting the passband signal by fc such that
Removing the component at -2fc from yS(t) leaves the baseband signal representation, y(t), which is given as
The expression for y(t) can be rewritten as , where . Expressing y(t) this way implies that the input signal is a scaled version of the derivative of the phase, ϕ(t).
To recover the input signal from y(t), use a baseband delay demodulator, as this figure shows.

References
[1] Hatai, I., and I. Chakrabarti. “A New High-Performance Digital FM Modulator and Demodulator for Software-Defined Radio and Its FPGA Implementation.” International Journal of Reconfigurable Computing (December 25, 2011): 1–10. https://doi.org/10.1155/2011/342532.
[2] Taub, H., and D. Schilling. Principles of Communication Systems. McGraw-Hill Series in Electrical Engineering, 142–55. New York: McGraw-Hill, 1971.
Extended Capabilities
Version History
Introduced in R2015a