Punctured Convolutional Coding

Introduction

This example shows how to simulate a communication system consisting of a random binary source, a convolutional encoder, a BPSK modulator, an additive white Gaussian noise (AWGN) channel, and a Viterbi decoder. In this example, you simulate the system, obtain BER curves, and compare the curves to a theoretical bound.

Initialization

Convolutional Encoding with Puncturing

Create a comm.ConvolutionalEncoder System object™ with a code rate of 1/2 and a constraint length of 7. The encoder takes 1-bit symbols as inputs and generates 2-bit symbols as outputs. For 3-bit message word inputs, the encoder generates 6-bit codeword outputs.

convEncoder = comm.ConvolutionalEncoder(poly2trellis(7,[171 133]));

Specify a puncture pattern to create a rate 3/4 code from the previous rate 1/2 code using the puncture pattern vector [1;1;0;1;1;0]. The ones in the puncture pattern vector indicate that bits in positions 1, 2, 4, and 5 are transmitted, while the zeros indicate that bits in positions 3 and 6 are punctured, or removed, from the transmitted signal. Now, for every 3 bits of input, the punctured code generates 4 bits of output rather than 6. The puncturing results in a rate 3/4 code. Because 3-bit inputs get converted into 6-bit outputs by the rate 1/2 convolutional encoder, the length of the puncture pattern vector must be an integer multiple of 6.

To specify the puncture pattern, set the PuncturePatternSource property to Property and the PuncturePattern property to [1;1;0;1;1;0].

convEncoder.PuncturePatternSource = 'Property';
convEncoder.PuncturePattern = [1;1;0;1;1;0];

Viterbi Decoding with Depuncturing

Configure a comm.ViterbiDecoder System object to decode the punctured code from the convolutional encoder. This example assumes unquantized inputs to the Viterbi decoder, so set the InputFormat property to Unquantized.

vitDecoder = comm.ViterbiDecoder( ...
    poly2trellis(7,[171 133]), ...
    InputFormat='Unquantized');

In general, the puncture pattern vectors you use for the convolutional encoder and Viterbi decoder must be the same. Set the corresponding properties for the Viterbi decoder.

Because the transmission does not include the punctured bits, the signal has no information to indicate their values. As a result, the decoding process ignores them.

vitDecoder.PuncturePatternSource = 'Property';
vitDecoder.PuncturePattern = convEncoder.PuncturePattern;

Set the traceback depth of the Viterbi decoder. For a rate 1/2 code with no puncturing, a typical traceback depth of a Viterbi decoder is 40. Decoding punctured codes requires a higher value to give the decoder enough data to resolve the ambiguities introduced by the punctures. Set a traceback depth of 96 using the TracebackDepth property. For more information about estimating the traceback depth, see Traceback Depth Estimates.

vitDecoder.TracebackDepth = 96;

Error Rate Calculation

Create a comm.ErrorRate calculator System object to compare the decoded output bits to the original transmitted bits. The output of the error rate calculator object is a three-element vector containing the calculated bit error rate, the number of errors observed, and the number of bits processed. The Viterbi decoder creates a delay in the output decoded bit stream equal to the traceback length. To account for this delay set the ReceiveDelay property of the error rate calculator equal to the Viterbi decoder traceback depth, which is 96.

errorCalc = comm.ErrorRate(ReceiveDelay=vitDecoder.TracebackDepth);

Processing Loop

Analyze the BER performance of the punctured coding system for different noise levels.

Uncoded and Coded Eb/No Ratios

Typically, you measure system performance according to the value of the energy per bit to noise power spectral density ratio (Eb/No) at the input of the channel encoder. This quantity is directly controlled by the systems engineer. Analyze the performance of the coding system for Eb/No values between 2 and 5 dB.

EbNoEncoderInput = 2:0.5:5; % in dB

The input to the AWGN channel is the modulated and encoded signal. Convert the noise power spectral density ratio at the input of the encoder to a signal-to-noise ratio (SNR) value at the output of the AWGN channel. Specify the coding rate of 3/4 to convert the Eb/No values so that the SNR corresponds to the energy ratio of the encoder output. This calculation assumes that the original signal power is unchanged by the encoding process. Since the system runs at the symbol rate, set the SamplesPerSymbol property to 1. Because this example uses BPSK modulation, the energy per bit to noise power spectral density ratio (Eb/No) and the energy per symbol to noise power spectral density ratio (Es/No) are the same.

SNR = convertSNR(EbNoEncoderInput,'ebno',CodingRate=3/4,SamplesPerSymbol=1);

Simulation

To obtain BER performance results, transmit frames of 3000 bits through the communications system. The frame length must be an integer multiple of 3.

frameLength = 3000;

Set the number of errors or transmissions at which to stop the simulation for each Eb/No value. To improve the accuracy of the results, increase the target number of errors or the maximum number of transmissions.

targetErrors = 300;
maxNumTx = 5e6;

Create a 3-by-7 matrix for storing the simulated BER results, BERVec.

BERVec = zeros(3,length(SNR));

Calculate the BER for each Eb/No value in 2:0.5:5 and store it in BERVec. This process takes a few seconds.

for n=1:length(SNR)
  reset(errorCalc)
  reset(convEncoder)
  reset(vitDecoder)
  while (BERVec(2,n) < targetErrors) && (BERVec(3,n) < maxNumTx)
    % Generate binary frame
    data = randi([0 1],frameLength,1);
    % Convolutionally encode the data
    encData = convEncoder(data);
    % Modulate the encoded data using M-PSK method
    modData = pskmod(encData,2);
    % Pass the modulated signal through an AWGN channel
    channelOutput = awgn(modData,SNR(n));
    % Pass the real part of the channel complex outputs 
    % as the unquantized input to the Viterbi decoder. 
    decData = vitDecoder(real(channelOutput));
    % Compute and accumulate errors
    BERVec(:,n) = errorCalc(data,decData);
  end
end

Simulation Results vs. Theoretical Curves

Compare the simulation results using an approximation of the bit error probability bound for a punctured code as per [1]. Compute an approximation of this bound using the first seven terms of the summation for Eb/No values in 2:0.5:5. The values for nerr are from Table 2 in [2].

dist = 5:11;
nerr = [42 201 1492 10469 62935 379644 2253373];
codeRate = 3/4;
bound = ...
    nerr*(1/6)*erfc(sqrt(codeRate*(10.0.^((2:.02:5)/10))'*dist))';

Plot the results. If the curve fitting algorithm fails, increase the target number of errors or maximum number of transmissions.

berfit(EbNoEncoderInput,BERVec(1,:)); % Curve-fit results
hold on;
semilogy((2:.02:5),bound,'g'); % Theoretical results
legend('Empirical BER', ...
    'Fit for simulated BER', ...
    'Theoretical bound on BER')
axis([1 6 10^-5 1])

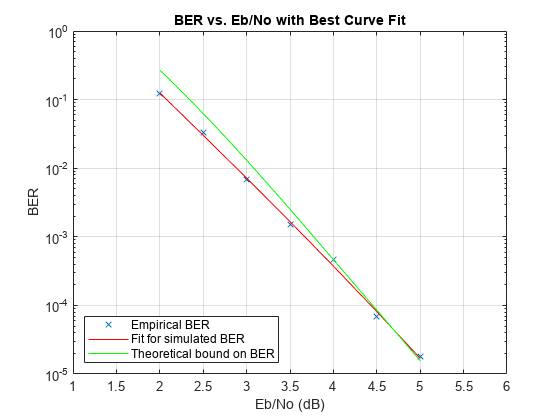
At lower bit error rates, the simulation can indicate error rates slightly above the bound. This result comes from simulation variance if you observe fewer than 500 bit errors, or from the finite traceback depth in the decoder.

References

[1] Yasuda, Y., K. Kashiki, and Y. Hirata, "High Rate Punctured Convolutional Codes for Soft Decision Viterbi Decoding," IEEE® Transactions on Communications, Vol. COM-32, March, 1984, pp. 315–319.

[2] Begin, G., Haccoun, D., and Paquin, C., "Further results on High-Rate Punctured Convolutional Codes for Viterbi and Sequential Decoding," IEEE Transactions on Communications, Vol. 38, No. 11, November, 1990, p. 1923.