inv

对动态系统模型求逆

语法

inv inv(sys,'min')

说明

inv 对以下输入/输出关系求逆

$y = G (s) u$

生成传递矩阵为 $H (s) = G {(s)}^{- 1}$ 的模型。

$u = H (s) y$

此操作仅适用于具有可逆前馈矩阵 D 的方形系统（输入数与输出数相同）。inv 对连续时间系统和离散时间系统都适用。

inv(sys,'min') 对 sys 求逆，以消除额外状态，获得状态数与 sys 或 A 相同的模型。对于 ss、genss 和 uss 模型，默认以隐式形式返回逆模型。对于稀疏模型，会忽略此选项，因为求逆通常会破坏稀疏性。如果需要，可使用 isproper 或 ss(sys,'explicit') 提取显式模型。

示例

假设

$H (s) = [\begin{matrix} 1 & \frac{1}{s + 1} \\ 0 & 1 \end{matrix}]$

在 MATLAB^® 提示符下键入

H = [1 tf(1,[1 1]);0 1]
Hi = inv(H)

以对其求逆。这些命令产生以下结果。

Transfer function from input 1 to output...
 #1:  1
 
 #2:  0
 
Transfer function from input 2 to output...
       -1
 #1:  -----
      s + 1
 
 #2:  1

您可以验证

H * Hi

结果为恒等传递函数（静态增益 I）。

限制

不要使用 inv 对如下反馈连接进行建模

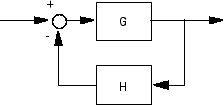
虽然将相应的闭环传递函数 ${(I + G H)}^{- 1} G$ 计算为以下形式看似合理，

inv(1+g*h) * g

但这通常会导致非最小闭环模型。例如，

g = zpk([],1,1)
h = tf([2 1],[1 0])
cloop = inv(1+g*h) * g

得到一个三阶闭环模型，且在 s = 1 处存在不稳定零极点相消。

cloop

Zero/pole/gain:
      s (s-1)
-------------------
(s-1) (s^2 + s + 1)

使用 feedback 可避免此类问题。

cloop = feedback(g,h)

Zero/pole/gain:
      s
-------------
(s^2 + s + 1)

版本历史记录

在 R2006a 之前推出