Absolute Stability for Quantized System

This example uses:

This example shows how to enforce absolute stability when a linear time-invariant system is in feedback interconnection with a static nonlinearity that belongs to a conic sector.

Feedback Connection

Consider the feedback connection as shown in Figure 1.

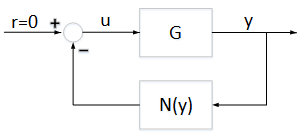
Figure 1: Feedback connection

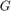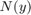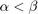$G$ is a linear time invariant system, and $N(y)$ is a static nonlinearity that belongs to a conic sector $[\alpha,\beta]$ (where $\alpha<\beta$ ); that is,

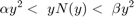
$\alpha y^2<~yN(y)<~\beta y^2$

For this example, 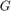$G$ is the following discrete-time system.

A = [0.9995, 0.0100, 0.0001;
    -0.0020, 0.9995, 0.0106;
          0,      0, 0.9978];
B = [0, 0.002, 0.04]';
C = [2.3948, 0.3303, 2.2726];
D = 0;
G = ss(A,B,C,D,0.01);

Sector Bounded Nonlinearity

In this example, the nonlinearity $N(y)$ is the logarithmic quantizer, which is defined as follows:

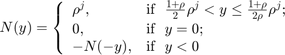
$N(y) = \left\{ \begin{array}{ll} \rho^j, & \mbox{if~ $
\frac{1+\rho}{2}\rho^j < y \leq \frac{1+\rho}{2\rho}\rho^j$};\\0, &
\mbox{if ~$y = 0$}; \\ -N(-y), & \mbox{if~ $y < 0$} \end{array} \right.
$

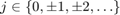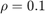where, $j\in \{0,\pm1,\pm2,\dots \}$ . This quantizer belongs to a sector bound $[\frac{2\rho}{1+\rho},\frac{2}{1+\rho}]$ . For example, if $\rho = 0.1$ , then the quantizer belongs to the conic sector [0.1818,1.8182].

% Quantizer parameter
rho = 0.1;
% Lower bound
alpha = 2*rho/(1+rho)
% Upper bound
beta = 2/(1+rho)

alpha =

    0.1818


beta =

    1.8182

Plot the sector bounds for the quantizer.

PlotSectorBound(rho)

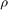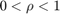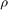$\rho$ represents the quantization density, where $0<\rho<1$ . If $\rho$ is larger, then the quantized value is more accurate. For more details about this quantizer, see [1].

Conic Sector Condition for Absolute Stability

The conic sector matrix for the quantizer is given by

$Q = \left(\begin{array}{cc} 1 & -\frac{\alpha+\beta}{2} \\
-\frac{\alpha+\beta}{2} & \alpha\beta \end{array}\right).$

To guarantee stability of the feedback connection in Figure 1, the linear system 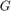$G$ needs to satisfy

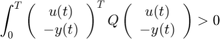
$\int_0^T \left(\begin{array}{c} u(t)\\-y(t)\end {array} \right)^T Q
\left(\begin{array}{c} u(t)\\-y(t)\end {array} \right) > 0$

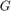where, $u$ and $y$ are the input and output of $G$ , respectively.

This condition can be verified by checking if the sector index, 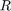$R$ , is less than 1.

Define the conic sector matrix for a quantizer with 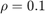$\rho = 0.1$ .

Q = [1,-(alpha+beta)/2;-(alpha+beta)/2,alpha*beta];

Get the sector index for Q and G.

R = getSectorIndex([1;-G],-Q)

R =

    1.8247

Since 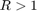$R>1$ , the closed-loop system is not stable. To see this instability, use the following Simulink® model.

mdl = 'DTQuantization';
open_system(mdl)

Run the Simulink model.

sim(mdl)
open_system('DTQuantization/output')

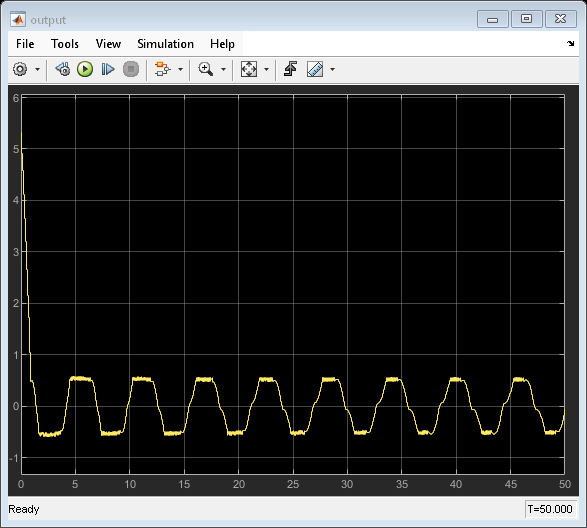
From the output trajectory, it can be seen that the closed-loop system is not stable. This is because the quantizer with 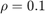$\rho = 0.1$ is too coarse.

Increase the quantization density by letting 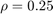$\rho = 0.25$ . The quantizer belongs to the conic sector [0.4,1.6].

% Quantizer parameter
rho = 0.25;
% Lower bound
alpha = 2*rho/(1+rho)
% Upper bound
beta = 2/(1+rho)

alpha =

    0.4000


beta =

    1.6000

Plot the sector bounds for the quantizer.

PlotSectorBound(rho)

Define the conic sector matrix for a quantizer with 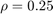$\rho = 0.25$ .

Q = [1,-(alpha+beta)/2;-(alpha+beta)/2,alpha*beta];

Get the sector index for Q and G.

R = getSectorIndex([1;-G],-Q)

R =

    0.9702

The quantizer with 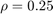$\rho = 0.25$ satisfies the conic sector condition for stability of the feedback connection since $R<1$ .

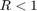Run the Simulink model with 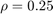$\rho = 0.25$ .

sim(mdl)
open_system('DTQuantization/output')

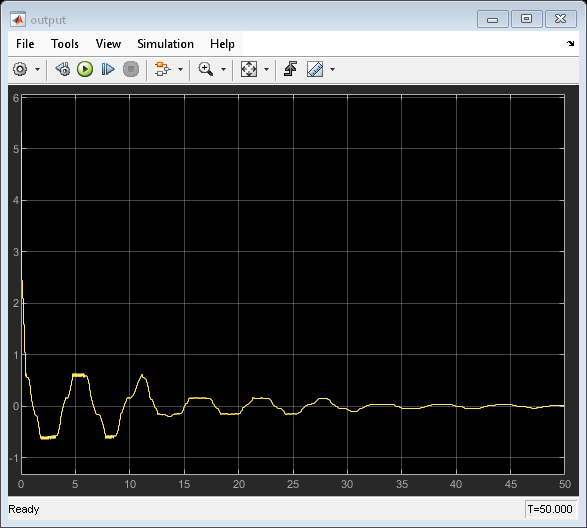
As indicated by the sector index, the closed-loop system is stable.

Reference

[1] M. Fu and L. Xie,"The sector bound approach to quantized feedback control," IEEE Transactions on Automatic Control 50(11), 2005, 1698-1711.