分析 RLC 电路的响应

打开实时脚本

此示例说明如何使用 Control System Toolbox™ 函数分析常见 RLC 电路的时间和频率响应随其物理参数变化的函数关系。

带通 RLC 网络

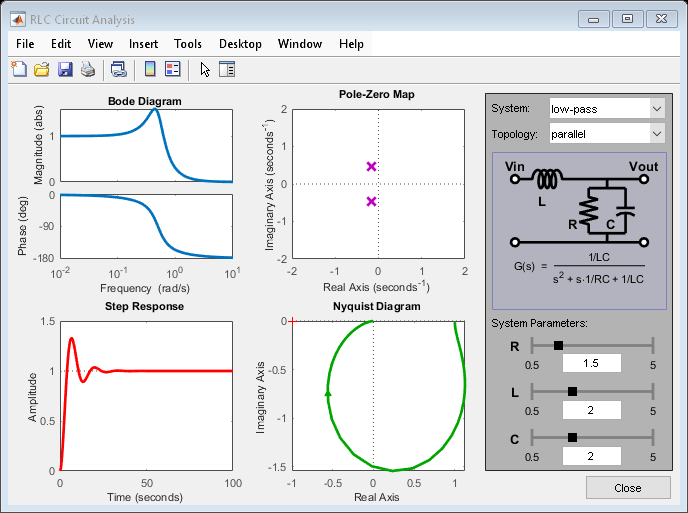
下图显示了带通 RLC 电路的并联型。

rlc_01.png

从输入到输出电压的传递函数为：

G(s)=s/(RC)s2+s/(RC)+1/(LC)

乘积 LC 控制带通频率，而 RC 控制通带的窄度。要构建调节到频率为 1 弧度/秒的带通滤波器，请设置 L=C=1 并使用 R 来调节滤波器频带。

分析电路的频率响应

波特图是研究 RLC 网络带通特性的便捷工具。请使用 tf 指定值为 R=L=C=1 的电路传递函数。

R = 1; L = 1; C = 1;
G = tf([1/(R*C) 0],[1 1/(R*C) 1/(L*C)])
G =
 
       s
  -----------
  s^2 + s + 1
 
Continuous-time transfer function.
Model Properties

绘制电路的频率响应。

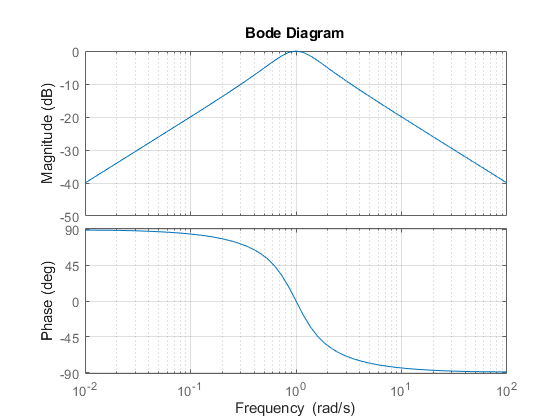
bodeplot(G)
grid on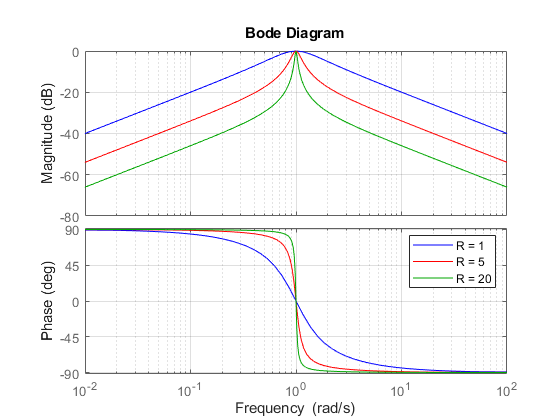

MATLAB figure

与预期相符，RLC 滤波器在频率为 1 弧度/秒时具有最大增益。然而，在距该频率半个十倍频程处，衰减仅为 -10dB。要获得更窄的通带，请尝试按如下方式增加 R 的值。

R1 = 5;
G1 = tf([1/(R1*C) 0],[1 1/(R1*C) 1/(L*C)]);
R2 = 20;
G2 = tf([1/(R2*C) 0],[1 1/(R2*C) 1/(L*C)]);

bodeplot(G,"b",G1,"r",G2,"g")
grid on
legend("R = 1","R = 5","R = 20");

MATLAB figure

电阻器值 R=20 使滤波器围绕 1 弧度/秒的目标频率呈现窄带调节。

分析电路的时间响应

可以通过对该滤波器如何变换频率为 0.9、1 和 1.1 弧度/秒的正弦波进行仿真来确认电路 G2 (R=20) 的衰减特性。

t = 0:0.05:250;
subplot(3,1,1)
lp1 = lsimplot(G2,sin(t),t);
lp1.Title.FontSize = 8;
lp1.XLabel.FontSize = 8;
lp1.YLabel.FontSize = 8;
title("w = 1")
subplot(3,1,2)
lp2 = lsimplot(G2,sin(0.9*t),t);
lp2.Title.FontSize = 8;
lp2.XLabel.FontSize = 8;
lp2.YLabel.FontSize = 8;
title("w = 0.9")
subplot(3,1,3)
lp3 = lsimplot(G2,sin(1.1*t),t);
lp3.Title.FontSize = 8;
lp3.XLabel.FontSize = 8;
lp3.YLabel.FontSize = 8;
title("w = 1.1")

MATLAB figure

频率为 0.9 和 1.1 弧度/秒的波有大幅衰减。一旦瞬态消失，频率为 1 弧度/秒的波就会保持不变。较长的瞬态是由滤波器的低阻尼极点造成的，遗憾的是，窄通带需要这些极点。

damp(pole(G2))
                                                                        
         Pole              Damping       Frequency       Time Constant  
                                       (rad/TimeUnit)     (TimeUnit)    
                                                                        
 -2.50e-02 + 1.00e+00i     2.50e-02       1.00e+00          4.00e+01    
 -2.50e-02 - 1.00e+00i     2.50e-02       1.00e+00          4.00e+01

另请参阅

| |

主题