换热器的温度控制

此示例说明如何设计反馈和前馈补偿器，以通过换热器调节化学反应器的温度。

换热器过程

下图描绘了一个名为搅拌罐 (stirring tank) 的化学反应器。顶部入口输送要在罐内混合的液体。必须通过调节其控制阀门，改变供应给换热器（底部管道）的蒸汽量，使罐内液体温度保持恒定。入口流体温度的变化是该过程的主要扰动源。

使用测量数据对换热器动态特性进行建模

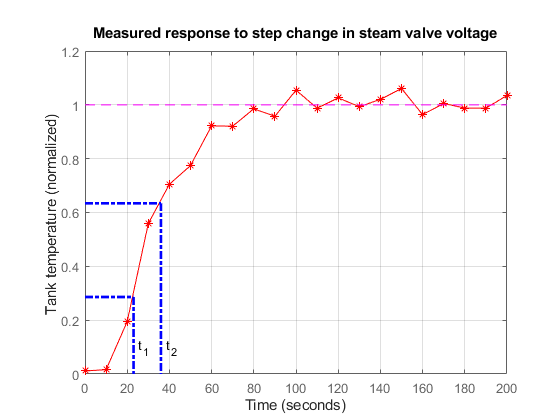
为推导换热器特征的一阶加纯滞后模型，在阀门电压 V 中注入阶跃扰动，并记录罐内温度 T 随时间的变化。加载并绘制试验数据。

load("step_data.mat","tData","yData")

plot(tData,yData,"r*-")
xlim([0 200])
ylim([0 1.2])
ylabel("Tank temperature (normalized)")
xlabel ("Time (seconds)")
grid on;
title("Measured Step Response");

hold on
t1 = 23;
t2 = 36;
plot([t1 t1],[0 0.283],"b--",LineWidth=2)
plot([0 t1],[0.283 0.283],"b--",LineWidth=2)
annotation("textbox",[0.22 0.26 0.1 0.1], ...
    String="t1",Color="b",EdgeColor="none")
plot([t2 t2],[0 0.632],"b--",LineWidth=2)
plot([0 t2],[0.632 0.632],"b--",LineWidth=2)
annotation("textbox",[0.28 0.48 0.1 0.1], ...
    String="t2",Color="b",EdgeColor="none")

Figure contains an axes object. The axes object with title Measured Step Response, xlabel Time (seconds), ylabel Tank temperature (normalized) contains 5 objects of type line.

值 t1 和 t2 分别是响应达到其最终值的 28.3% 和 63.2% 的时间。您可以使用这些值估计换热器的时间常数 tau 和滞后时间 theta。

tau = 3/2 * ( t2 - t1 )

tau = 
19.5000

theta = t2 - tau

theta = 
16.5000

通过比较一阶加纯滞后响应与测量响应，验证计算结果。

s = tf("s");
Gp = exp(-theta*s)/(1+tau*s);

将 Gp 的阶跃响应与试验数据绘制在同一坐标区上。

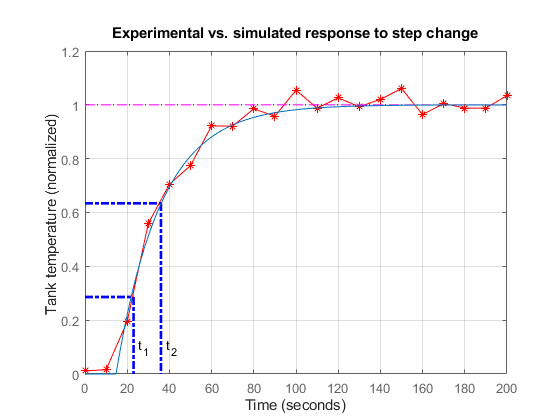
sp = stepplot(Gp,0:1:200);
xlim([0 200])
ylim([0 1.2])
ylabel("Tank temperature (normalized)")
title("Experimental and Simulated Step Response")
grid on

MATLAB figure

模型响应与试验数据吻合良好。可进行类似的碰撞测试试验来估计对入口流体温度阶跃扰动的一阶响应。有了换热器和入口扰动的模型后，您就可以设计控制算法了。

反馈控制

下图显示了开环过程的模块图。

传递函数

$G_{p} (s) = \frac{e^{- 14.7 s}}{21.3 s + 1}$

用于建模驱动蒸汽阀门开度的电压 V 的变化对罐内温度 T 的影响，而传递函数

$G_{d} (s) = \frac{e^{- 35 s}}{25 s + 1}$

用于建模入口流体温度变化 d 对 T 的影响。为将罐内温度 T 调节到给定设定点 Tsp 附近，您可以使用以下反馈架构控制阀门开度（电压 V）。

在此配置中，比例积分 (PI) 控制器

$C (s) = K_{c} (1 + \frac{1}{τ_{c} s})$

根据期望温度与测量温度之间的差距 Tsp-T 计算电压 V。您可以使用 ITAE 公式选择合适的控制器参数。

$K_{c} = 0.859 (θ / τ)^{- 0.977}, τ_{c} = (θ / τ)^{0.680} τ / 0.674$

Kc = 0.859 * (theta / tau)^(-0.977)

Kc = 
1.0113

tauc = ( tau / 0.674 ) * ( theta / tau )^0.680

tauc = 
25.8250

C = Kc * (1 + 1/(tauc*s));

为观察 ITAE 控制器的性能，可闭合反馈环并仿真对设定点变化的响应。

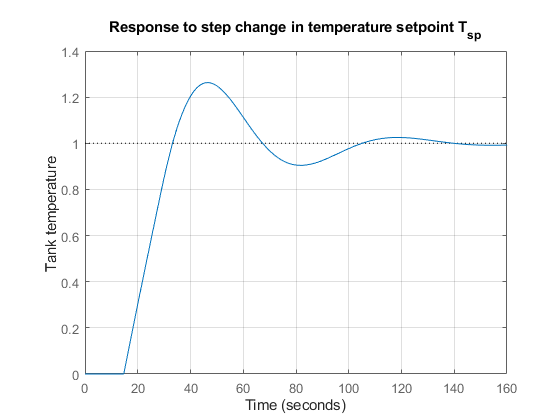
figure
Tfb = feedback(ss(Gp*C),1);
stepplot(Tfb,0:1:200)
hold on
plot(tData,yData,"r*-")
title("Response to Step Change in Temperature Setpoint")
ylabel("Tank temperature (normalized)")
grid on

MATLAB figure

响应速度较快，但存在一定超调。查看稳定裕度可知，增益裕度较小。

figure
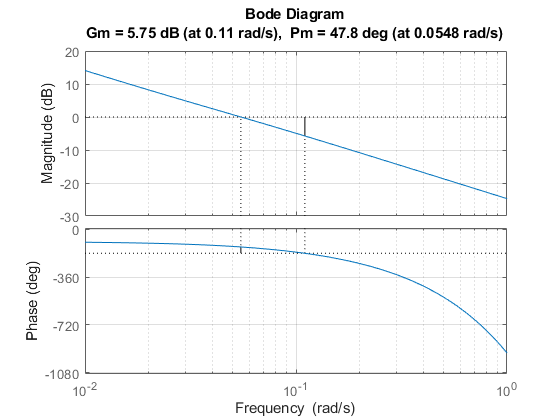
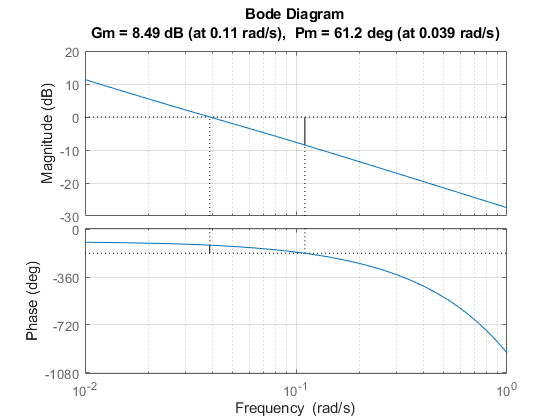
margin(Gp*C)
grid on

MATLAB figure

减小比例增益 Kc 可增强稳定性，但会导致性能下降。

C1 = 0.9 * (1 + 1/(tauc*s));  % reduce Kc from 1.23 to 0.9
margin(Gp*C1)
grid on

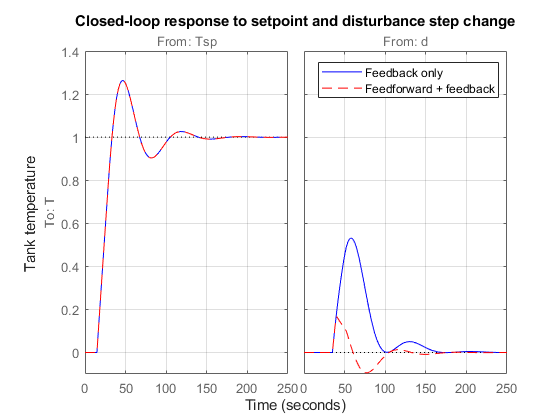
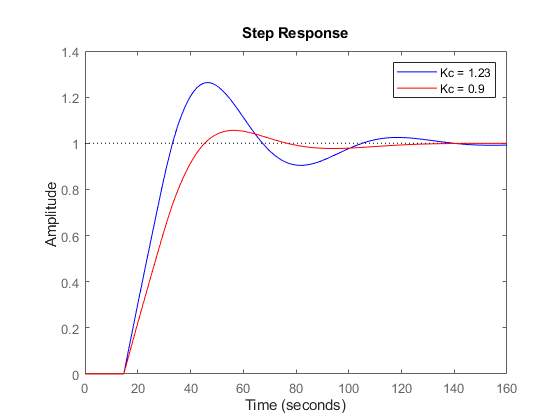
MATLAB figure

figure
stepplot(Tfb,"r",feedback(ss(Gp*C1),1),"b",0:1:200)
title("Response to Step Change in Temperature Setpoint")
ylabel("Tank temperature (normalized)")
legend("Kc = 1.23","Kc = 0.9");
grid on

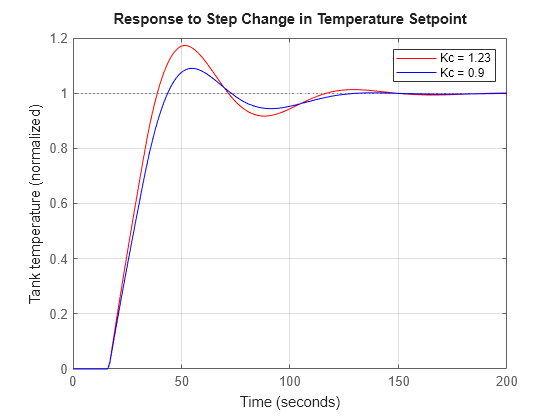
MATLAB figure

前馈控制

前面讲到，入口流体温度变化是罐内温度波动的主要来源。为抑制此类扰动，除反馈控制之外，还可以采用下图所示的前馈控制架构：

在此配置中，前馈控制器 F 利用入口流体温度的测量值调节蒸汽阀门开度（电压 V）。因此，前馈控制可预见并预先消除入口流体温度变化的影响。

通过直接计算可知，从温度扰动 d 到罐内温度 T 的总传递函数为：

$T = (G_{p} F + G_{d}) d$

理想的抗扰需满足：

$G_{p} F + G_{d} = 0 \to F = - \frac{G_{d}}{G_{p}} = - \frac{21.3 s + 1}{25 s + 1} e^{- 20.3 s}$

在现实中，建模不准确会导致无法实现完全抗扰，但前馈控制仍能最大限度地减小入口流体温度变化引起的温度波动。为更清晰地了解前馈方案的性能，可将理想前馈延迟增加 5 秒，并仿真对入口流体温度变化阶跃变化的响应：

Gd = exp(-35*s)/(25*s+1);
F = -(21.3*s+1)/(25*s+1) * exp(-25*s);
Tff = Gp * ss(F) + Gd;   % d->T transfer with feedforward control

figure
stepplot(Tff)
title("Effect of Step Disturbance in Inflow Temperature")
ylabel("Tank temperature (normalized)")
grid on

MATLAB figure

前馈-反馈组合控制

通常，反馈控制擅长设定点跟踪，而前馈控制可帮助抑制可测扰动。接下来，我们来看看两种控制方案组合使用的优势。相应的控制架构如下图所示。

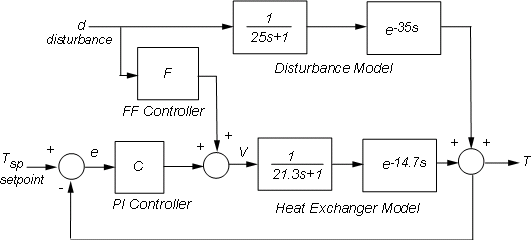
使用 connect 构建从 Tsp,d 到 T 的相应闭环模型。首先为每个模块的输入和输出通道命名，然后使用 connect 连接模块图。

Gd.u = "d";
Gd.y = "Td";
Gp.u = "V";
Gp.y = "Tp";
F.u = "d";
F.y = "Vf";
C.u = "e";
C.y = "Vc";
Sum1 = sumblk("e = Tsp - T");
Sum2 = sumblk("V = Vf + Vc");
Sum3 = sumblk("T = Tp + Td");
Tffb = connect(Gp,Gd,C,F,Sum1,Sum2,Sum3,{"Tsp","d"},"T");

为比较采用前馈控制与不采用前馈的闭环响应，请计算仅反馈配置下相应的闭环传递函数。

C.u = "e";
C.y = "V";
Tfb = connect(Gp,Gd,C,Sum1,Sum3,{"Tsp","d"},"T");

比较两种设计。

stepplot(Tfb,"b",Tffb,"r--");
title("Closed-loop Step Response to Setpoint and Disturbance Change");
ylabel("Tank temperature (normalized)")
legend("Feedback only","Feedforward + feedback");
grid on

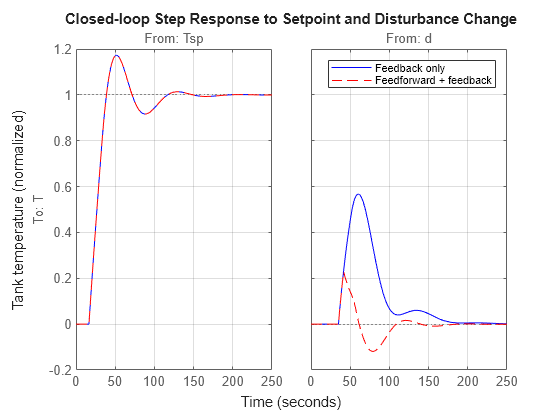
MATLAB figure

两种设计在设定点跟踪方面性能相同，但加入前馈控制后，抗扰性能有所提升。该结果在闭环波特图中也可体现。

figure
bodemag(Tfb,"b",Tffb,"r--",{1e-3,1e1})
legend("Feedback only","Feedforward + feedback",Location="SouthEast");

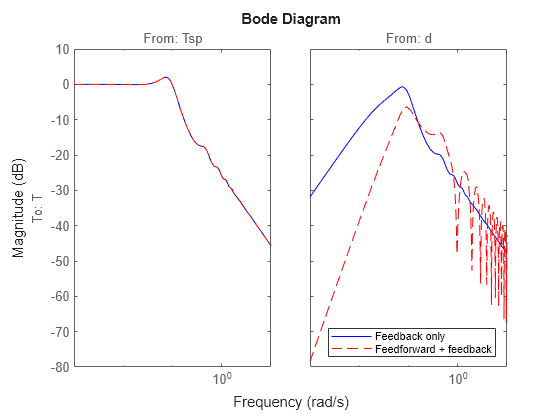
MATLAB figure

交互式仿真

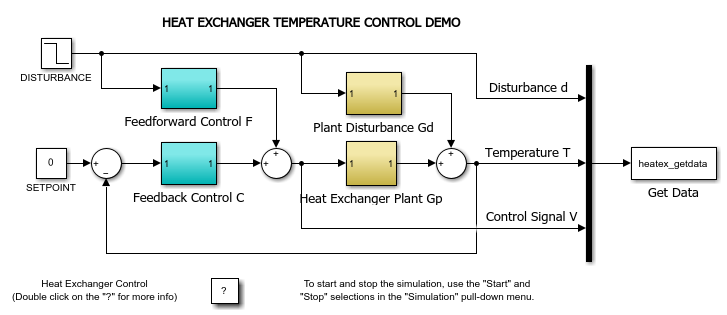
您可以使用 HeatExchanger 以交互式方式探索换热器系统的控制策略。该 App 基于 App 设计工具开发，使用 heatex_sim Simulink® 模型对换热器进行仿真。

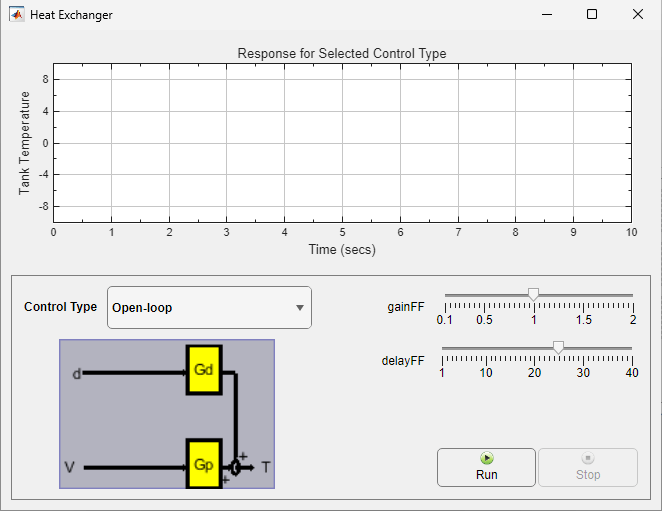
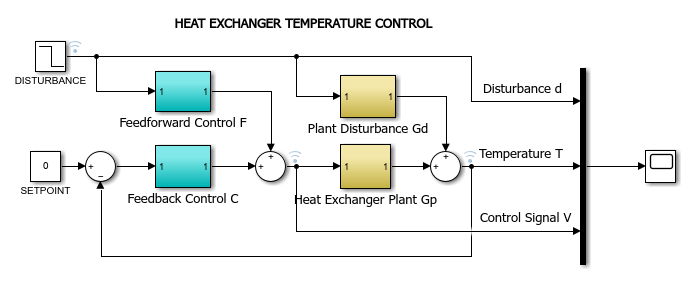
借助该 App，您可以使用开环控制、前馈控制、反馈控制和前馈-反馈组合控制对换热器进行仿真。您还可调整前馈控制器的增益和延迟参数。

要运行该 App，请使用以下命令。

HeatExchanger