Constructing and Working with ppform Splines
Constructing a ppform
A piecewise-polynomial is usually constructed by some command, through a process of interpolation or approximation, or conversion from some other form e.g., from the B-form, and is output as a variable. But it is also possible to make one up from scratch, using the statement
pp = ppmak(breaks,coefs)
For example, if you enter pp=ppmak(-5:-1,-22:-11),
or, more explicitly,
breaks = -5:-1; coefs = -22:-11; pp = ppmak(breaks,coefs);
you specify the uniform break sequence
-5:-1 and the coefficient sequence
-22:-11. Because this break
sequence has 5 entries, hence 4 break intervals, while the coefficient
sequence has 12 entries, you have, in effect, specified a piecewise-polynomial
of order 3 (= 12/4). The command
fnbrk(pp)
prints out all the constituent parts of this piecewise-polynomial, as follows:
breaks(1:l+1)
-5 -4 -3 -2 -1
coefficients(d*l,k)
-22 -21 -20
-19 -18 -17
-16 -15 -14
-13 -12 -11
pieces number l
4
order k
3
dimension d of target
1 Further, fnbrk can be used to supply each
of these parts separately. But the point of Curve Fitting Toolbox™ spline
functionality is that you usually need not concern yourself with these
details. You simply use pp as an argument to commands
that evaluate, differentiate, integrate, convert, or plot the piecewise-polynomial
whose description is contained in pp.
Working With ppform Splines
Here are some functions for operations you can perform on a piecewise-polynomial.
| Evaluates |
| Differentiates |
| Differentiates in the direction |
| Integrates |
| Finds the minimum value in given interval |
| Finds the zeros in the given interval |
| Pulls out the |
| |
| Extends outside its basic interval by polynomial of specified order |
| Plots on given interval |
| Converts to B-form |
| Inserts additional breaks |
Inserting additional breaks comes in handy when you want to
add two piecewise-polynomials with different breaks, as is done in
the command fncmb.
Example ppform
Execute the following commands to create and plot the particular piecewise-polynomial (ppform) described in the Constructing a ppform section.
Create the piecewise-polynomial with break sequence
-5:-1and coefficient sequence-22:-11:pp=ppmak(-5:-1,-22:-11)
Create the basic plot:
x = linspace(-5.5,-.5,101); plot(x, fnval(pp,x),'x')
Add the break lines to the plot:
breaks=fnbrk(pp,'b'); yy=axis; hold on for j=1:fnbrk(pp,'l')+1 plot(breaks([j j]),yy(3:4)) end
Superimpose the plot of the polynomial that supplies the third polynomial piece:
plot(x,fnval(fnbrk(pp,3),x),'linew',1.3) set(gca,'ylim',[-60 -10]), hold off
A Piecewise-Polynomial Function, Its Breaks, and the Polynomial Giving Its Third Piece
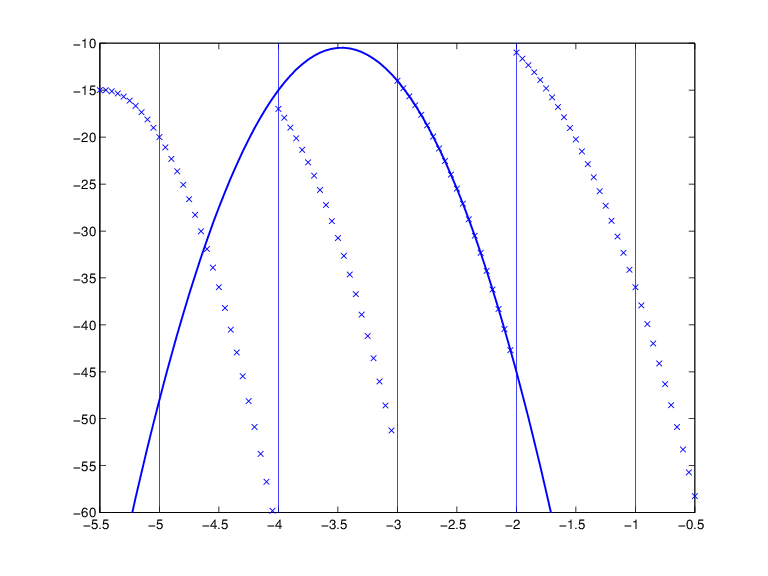
The figure above is the final picture. It shows the piecewise-polynomial as a sequence of points and, solidly on top of it, the polynomial from which its third polynomial piece is taken. It is quite noticeable that the value of a piecewise-polynomial at a break is its limit from the right, and that the value of the piecewise-polynomial outside its basic interval is obtained by extending its leftmost, respectively its rightmost, polynomial piece.
While the ppform of a piecewise-polynomial is efficient for evaluation, the construction of a piecewise-polynomial from some data is usually more efficiently handled by determining first its B-form, i.e., its representation as a linear combination of B-splines.