Surface Fitting with Custom Equations to Biopharmaceutical Data

Open Live Script

This example shows how to use Curve Fitting Toolbox™ to fit response surfaces to some anesthesia data to analyze drug interaction effects. Response surface models provide a good method for understanding the pharmacodynamic interaction behavior of drug combinations.

This data is based on the results in this paper: Kern SE, Xie G, White JL, Egan TD. Opioid-hypnotic synergy: A response surface analysis of propofol-remifentanil pharmacodynamic interaction in volunteers. Anesthesiology 2004; 100: 1373-81.

Anesthesia is typically at least a two-drug process, consisting of an opioid and a sedative hypnotic. This example uses Propofol and Reminfentanil as drug class prototypes. Their interaction is measured by four different measures of the analgesic and sedative response to the drug combination. Algometry, Tetany, Sedation, and Laryingoscopy comprise the four measures of surrogate drug effects at various concentration combinations of Propofol and Reminfentanil.

The following code, using Curve Fitting Toolbox methods, reproduces the interactive surface building with the Curve Fitting Tool described in Surface Fitting to Biopharmaceutical Data.

Load Data

Load the data from file.

data = importdata( 'OpioidHypnoticSynergy.txt' );
Propofol      = data.data(:,1);
Remifentanil  = data.data(:,2);
Algometry     = data.data(:,3);
Tetany        = data.data(:,4);
Sedation      = data.data(:,5);
Laryingoscopy = data.data(:,6);

Create the Model Fit Type

You can use the fittype function to define the model from the paper, where CA and CB are the drug concentrations, and IC50A, IC50B, alpha, and n are the coefficients to be estimated. Create the model fit type.

ft = fittype( 'Emax*( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) * ( CB/IC50B ) )^n /(( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) * ( CB/IC50B ) )^n  + 1 )', ...
    'independent', {'CA', 'CB'}, 'dependent', 'z', 'problem', 'Emax' )

ft = 
     General model:
     ft(IC50A,IC50B,alpha,n,Emax,CA,CB) = Emax*( CA/IC50A + CB/IC50B + alpha*( 
                    CA/IC50A ) * ( CB/IC50B ) )^n /(( CA/IC50A + CB/IC50B 
                    + alpha*( CA/IC50A ) * ( CB/IC50B ) )^n  + 1 )

Assume Emax = 1 because the effect output is normalized.

Emax = 1;

Set Fit Options

Set fit options for robust fitting, bounds, and start points.

opts = fitoptions( ft );
opts.Lower = [0, 0, -5, -0];
opts.Robust = 'LAR';
opts.StartPoint = [0.0089, 0.706, 1.0, 0.746];

Fit and Plot a Surface for Algometry

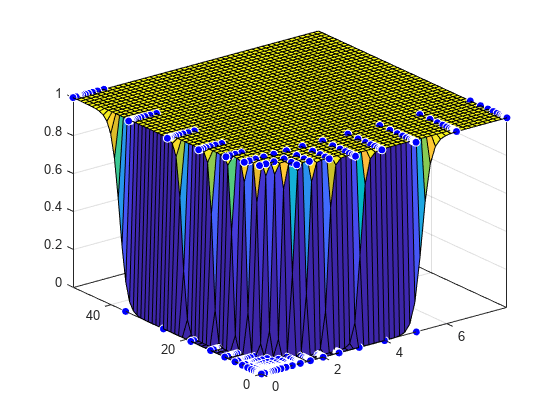
[f, gof] = fit( [Propofol, Remifentanil], Algometry, ft,...
    opts, 'problem', Emax )

Success, but fitting stopped because change in residuals less than tolerance (TolFun).

f = 
     General model:
     f(CA,CB) = Emax*( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) * ( CB/IC50B 
                    ) )^n /(( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) 
                    * ( CB/IC50B ) )^n  + 1 )
     Coefficients (with 95% confidence bounds):
       IC50A =       4.149  (4.123, 4.174)
       IC50B =       9.044  (8.971, 9.118)
       alpha =       8.502  (8.316, 8.688)
       n =       8.289  (8.131, 8.446)
     Problem parameters:
       Emax =           1

gof = struct with fields:
           sse: 0.0842
       rsquare: 0.9991
           dfe: 393
    adjrsquare: 0.9991
          rmse: 0.0146

plot( f, [Propofol, Remifentanil], Algometry );

Figure contains an axes object. The axes object contains 2 objects of type line, surface. One or more of the lines displays its values using only markers

Fit a Surface to Tetany

Reuse the same fittype to create a response surface for tetany.

[f, gof] = fit( [Propofol, Remifentanil], Tetany, ft, opts, 'problem', Emax )

f = 
     General model:
     f(CA,CB) = Emax*( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) * ( CB/IC50B 
                    ) )^n /(( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) 
                    * ( CB/IC50B ) )^n  + 1 )
     Coefficients (with 95% confidence bounds):
       IC50A =       4.544  (4.522, 4.567)
       IC50B =       21.22  (21.04, 21.4)
       alpha =       14.94  (14.67, 15.21)
       n =       6.132  (6.055, 6.209)
     Problem parameters:
       Emax =           1

gof = struct with fields:
           sse: 0.0537
       rsquare: 0.9993
           dfe: 393
    adjrsquare: 0.9993
          rmse: 0.0117

plot( f, [Propofol, Remifentanil], Tetany );

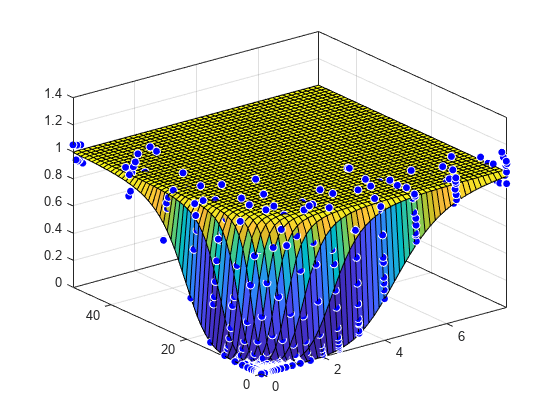
Figure contains an axes object. The axes object contains 2 objects of type line, surface. One or more of the lines displays its values using only markers

Fit a Surface to Sedation

[f, gof] = fit( [Propofol, Remifentanil], Sedation, ft, opts, 'problem', Emax )

f = 
     General model:
     f(CA,CB) = Emax*( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) * ( CB/IC50B 
                    ) )^n /(( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) 
                    * ( CB/IC50B ) )^n  + 1 )
     Coefficients (with 95% confidence bounds):
       IC50A =       1.843  (1.838, 1.847)
       IC50B =        13.7  (13.67, 13.74)
       alpha =       1.986  (1.957, 2.015)
       n =       44.27  (42.56, 45.98)
     Problem parameters:
       Emax =           1

gof = struct with fields:
           sse: 0.0574
       rsquare: 0.9994
           dfe: 393
    adjrsquare: 0.9994
          rmse: 0.0121

plot( f, [Propofol, Remifentanil], Sedation );

Figure contains an axes object. The axes object contains 2 objects of type line, surface. One or more of the lines displays its values using only markers

Fit a Surface to Laryingoscopy

[f, gof] = fit( [Propofol, Remifentanil], Laryingoscopy, ft, opts, 'problem', Emax )

f = 
     General model:
     f(CA,CB) = Emax*( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) * ( CB/IC50B 
                    ) )^n /(( CA/IC50A + CB/IC50B + alpha*( CA/IC50A ) 
                    * ( CB/IC50B ) )^n  + 1 )
     Coefficients (with 95% confidence bounds):
       IC50A =       5.192  (5.177, 5.207)
       IC50B =       37.77  (37.58, 37.97)
       alpha =       19.67  (19.48, 19.86)
       n =          37  (35.12, 38.87)
     Problem parameters:
       Emax =           1

gof = struct with fields:
           sse: 0.1555
       rsquare: 0.9982
           dfe: 393
    adjrsquare: 0.9982
          rmse: 0.0199

plot( f, [Propofol, Remifentanil], Laryingoscopy );

Figure contains an axes object. The axes object contains 2 objects of type line, surface. One or more of the lines displays its values using only markers