Create Basket Summary and Efficient Trading Frontier
This example shows how to evaluate trading cost and risk components for a basket using transaction cost analysis from the Kissell Research Group. To create a basket summary, estimate trading costs for the entire basket using basket optimization techniques, and then calculate risk statistics for the basket. Using the basket summary, you can provide brokers and third parties with enough information to assess the overall execution costs and trading difficulty of the basket. The basket summary enables providing transaction information without revealing the actual orders. Another way brokers use a basket summary is to assess a fair value principal bid estimate. A principal bid is a transaction where the broker charges a bid premium that is higher than the associated commission. Brokers present this transaction with guaranteed completion for a given price.
In this example, you can see a basket summary analysis table and a principal bid summary. The basket summary provides trading cost estimates for the basket across different categories, such as side, market capitalization, and market sector. The principal bid summary contains the efficient trading frontier that provides the different estimated trading costs for different time periods. The efficient trading frontier shows how cost and risk change by trading more aggressively or passively. With passive trading, market impact decreases as timing risk increases. With aggressive trading, market impact increases as timing risk decreases.
The code in this example depends on the output data from the example Optimize Trade Schedule Trading Strategy for Basket. Run the code in that example first and then run the code in this example.
To access the example code, enter edit
KRGBasketAnalysisExample.m at the command line.
After executing the code in this example, you can submit an order for execution using Bloomberg®, for example.
Estimate Trading Costs in Basket
Determine the covariance matrix. Covariance indicates how the prices of stocks in the basket relate to each other.
% Covariance matrix is annualized covariance matrix in decimals. % Convert to ($/Shares)^2 units for the trade period, this matrix is for a % two-sided portfolio, buys and sells or long and short. diagPrice = diag(TradeDataTradeOpt.Price); C1 = TradeDataTradeOpt.SideIndicator * TradeDataTradeOpt.SideIndicator' .* ... diagPrice * CovarianceTradeOpt * diagPrice; % Covariance Matrix in $/Share^2 by Day CD = diagPrice * CovarianceTradeOpt * diagPrice; % compute Covariance Matrix in ($/share)^2 CD = CD / k.TradeDaysInYear; % scale to 1-day CD = TradeDataTradeOpt.SideIndicator * TradeDataTradeOpt.SideIndicator' ... .* CD;
Add the estimated trading costs from the trade schedule optimization to the basket data.
% Market impact in basis points TradeDataTradeOpt.MI = MI ./ (TradeDataTradeOpt.Shares .* ... TradeDataTradeOpt.Price) .* 10000; % Timing risk in basis points TradeDataTradeOpt.TR = TR ./ (TradeDataTradeOpt.Shares .* ... TradeDataTradeOpt.Price) .* 10000; % Percentage of volume, price appreciation and liquidity factor TradeDataTradeOpt.POV = POV; TradeDataTradeOpt.PA = PA; TradeDataTradeOpt.LF = liquidityFactor(k,TradeDataTradeOpt);
Calculate trading costs in basis points, cents per share, and dollars.
% Build optimal cost table OptimalCostTable = table(cell(3,1),zeros(3,1),zeros(3,1),zeros(3,1), ... zeros(3,1),'VariableNames',{'CostUnits','MI','PA','TotalCost','TR'}); OptimalCostTable.CostUnits(1) = {'Basis Points'}; OptimalCostTable.CostUnits(2) = {'Cents per Share'}; OptimalCostTable.CostUnits(3) = {'Dollars'}; % Market impact, OptimalCostTable.MI(1) = TotMI; OptimalCostTable.MI(2) = TotMI / 100 * mean(TradeDataTradeOpt.Price); OptimalCostTable.MI(3) = TotMI / 100 * (TradeDataTradeOpt.Shares' * ... TradeDataTradeOpt.Price); % Price appreciation OptimalCostTable.PA(1) = TotPA; OptimalCostTable.PA(2) = TotPA / 100 * mean(TradeDataTradeOpt.Price); OptimalCostTable.PA(3) = TotPA / 100 * (TradeDataTradeOpt.Shares' * ... TradeDataTradeOpt.Price); % Total cost OptimalCostTable.TotalCost(1) = TotMI + TotPA; OptimalCostTable.TotalCost(2) = (TotMI + TotPA) / 100 * mean(TradeDataTradeOpt.Price); OptimalCostTable.TotalCost(3) = (TotMI + TotPA) / 100 * ... (TradeDataTradeOpt.Shares' * TradeDataTradeOpt.Price); % Timing risk OptimalCostTable.TR(1) = TotTR; OptimalCostTable.TR(2) = TotTR / 100 * mean(TradeDataTradeOpt.Price); OptimalCostTable.TR(3) = TotTR / 100 * ... (TradeDataTradeOpt.Shares' * TradeDataTradeOpt.Price);
Display the optimal costs for the basket. Format the display output to show cents and dollars. Optimal costs are market impact, price appreciation, total cost, and timing risk.
format bank
OptimalCostTableOptimalCostTable =
3×5 table array
CostUnits MI PA TotalCost TR
_________________ ____________ ____ ____________ ____________
'Basis Points' 38.30 0.00 38.30 26.57
'Cents per Share' 14.88 0.00 14.88 10.32
'Dollars' 171134479.73 0.00 171134479.73 118710304.48
Determine Risk Components in Basket
Calculate risk statistics. The marginal contribution to risk captures the risk of changing one of the components in the basket, such as the number of shares. The risk contribution is the risk for each trade in the basket.
% Portfolio Risk in Dollars PortfolioRisk = sqrt(TradeDataTradeOpt.Shares' * CD * ... TradeDataTradeOpt.Shares); % MCR and RC calculations PortfolioRiskMCR = zeros(numberStocks,1); PortfolioRiskRC =zeros(numberStocks,1); SharesMCR = TradeDataTradeOpt.Shares; SharesRC = TradeDataTradeOpt.Shares; for i = 1:numberStocks SharesMCR(i) = TradeDataTradeOpt.Shares(i) * 0.90; SharesRC(i) = 0; PortfolioRiskMCR(i) = sqrt(SharesMCR' * CD * SharesMCR); PortfolioRiskRC(i) = sqrt(SharesRC' * CD * SharesRC); end TradeDataTradeOpt.MCR = PortfolioRisk ./ PortfolioRiskMCR - 1; TradeDataTradeOpt.RC = PortfolioRisk ./ PortfolioRiskRC - 1;
Display the side, symbol, and number of shares for the safest trade in the basket using the risk contribution.
minrisk = min(TradeDataTradeOpt.RC); for i = 1:25 if TradeDataTradeOpt.RC(i) == minrisk idx = i; end end [TradeDataTradeOpt.Side(idx) TradeDataTradeOpt.Symbol(idx) ... TradeDataTradeOpt.Shares(idx)]
ans =
1×3 cell array
'B' 'ABC' [100000]The buy order of 100,000 shares of stock ABC contributes
the most overall portfolio risk.
Create Basket Report Summary
Create a table for the basket report summary.
% Get sector identifiers uniqueSectors = unique(TradeDataTradeOpt.Sector); numSectors = size(uniqueSectors,1); numGroups = 14 + size(uniqueSectors,1); % Using 14 categories plus number of sectors % Preallocate BasketReport table BasketReport = table; BasketReport.BasketCategory = cell(numGroups,1); BasketReport.Number = zeros(numGroups,1); BasketReport.Weight = zeros(numGroups,1); BasketReport.MI = zeros(numGroups,1); BasketReport.TR = zeros(numGroups,1); BasketReport.POV = zeros(numGroups,1); BasketReport.TradeTime = zeros(numGroups,1); BasketReport.PctADV = zeros(numGroups,1); BasketReport.Price = zeros(numGroups,1); BasketReport.Volatility = zeros(numGroups,1); BasketReport.Risk = zeros(numGroups,1); BasketReport.RC = zeros(numGroups,1); BasketReport.MCR = zeros(numGroups,1); BasketReport.Beta = zeros(numGroups,1); BasketReport.LF = zeros(numGroups,1); BasketReport.TotalValue = zeros(numGroups,1); BasketReport.BuyValue = zeros(numGroups,1); BasketReport.SellValue = zeros(numGroups,1); BasketReport.NetValue = zeros(numGroups,1); BasketReport.Shares = zeros(numGroups,1); BasketReport.BuyShares = zeros(numGroups,1); BasketReport.SellShares = zeros(numGroups,1);
Calculate the basket report summary.
Divide the trades in the basket into these categories:
Total— All trades in basketBuy— Buy tradesCover— Buy trades that cover a short positionSell— Sell tradesShort— Short trades<=1%— Trades that have percentage of average daily volume less than or equal to 1%1%-3%— Trades that have percentage of average daily volume between 1% and 3%3%-5%— Trades that have percentage of average daily volume between 3% and 5%5%-10%— Trades that have percentage of average daily volume between 5% and 10%10%-20%— Trades that have percentage of average daily volume between 10% and 20%>20%— Trades that have percentage of average daily volume greater than 20%LC— Large-capitalization stock tradesMC— Mid-capitalization stock tradesSC— Small-capitalization stock tradesConsumer Discretionary— Trades in the consumer discretionary industryConsumer Staples— Trades in the consumer staples industryEnergy— Trades in the energy industryFinancials— Trades in the financial industryHealth Care— Trades in the health care industryIndustrials— Trades in the industrial industryInformation Technology— Trades in the information technology industryMaterials— Trades in the materials industryTelecommunication Services— Trades in the telecommunication services industryUtilities— Trades in the utilities industry
For stocks in each category, calculate these values:
Weight— Total trade value weightMI— Weighted average market-impact costTR— Timing riskPOV— Weighted average percentage of volume rateTradeTime— Weighted average trade time to complete the orderPctADV— Weighted average order size (measured as percentage of average daily volume)Price— Weighted average share priceVolatility— Weighted average volatilityRisk— Portfolio riskRC— Risk contribution to the overall portfolio risk (shows the amount of risk that an order contributes to the basket)MCR— Marginal contribution to risk (shows the amount of risk that 10% of shares in the order contribute to the basket)Beta— Weighted average betaLF— Weighted average liquidity factorTotalValue— Total trade valueBuyValue— Total trade value of the buy transactionsSellValue— Total trade value of the sell transactionsNetValue— Difference between total trade value of the buy and sell transactionsShares— Number of sharesBuyShares— Number of shares to buySellShares— Number of shares to sell
% Fill table, indRecord is index of matching TradeData rows j = 0; for i = 1:24 switch i % Total case 1 indRecord = true(numberStocks,1); BasketReport.BasketCategory(i) = {'Total'}; % Side case 2 indRecord = strcmp(TradeDataTradeOpt.Side,'B') | ... strcmp(TradeDataTradeOpt.Side,'Buy'); BasketReport.BasketCategory(i) = {'Buy'}; case 3 indRecord = strcmp(TradeDataTradeOpt.Side,'C') | ... strcmp(TradeDataTradeOpt.Side,'Cover'); BasketReport.BasketCategory(i) = {'Cover'}; case 4 indRecord = strcmp(TradeDataTradeOpt.Side,'S') | ... strcmp(TradeDataTradeOpt.Side,'Sell'); BasketReport.BasketCategory(i) = {'Sell'}; case 5 indRecord = strcmp(TradeDataTradeOpt.Side,'SS') | ... strcmp(TradeDataTradeOpt.Side,'Short') | ... strcmp(TradeDataTradeOpt.Side,'Sell Short'); BasketReport.BasketCategory(i) = {'Short'}; % Liquidity Category case 6 % Percentage of average daily volume is less than 1 % indRecord = (TradeDataTradeOpt.PctADV <= 0.01); BasketReport.BasketCategory(i) = {'<=1%'}; case 7 % Percentage of average daily volume is between 1 and 3 % indRecord = (TradeDataTradeOpt.PctADV > 0.01 & ... TradeDataTradeOpt.PctADV <= 0.03); BasketReport.BasketCategory(i) = {'1%-3%'}; case 8 % Percentage of average daily volume is between 3 and 5 % indRecord = (TradeDataTradeOpt.PctADV > 0.03 & ... TradeDataTradeOpt.PctADV <= 0.05); BasketReport.BasketCategory(i) = {'3%-5%'}; case 9 % Percentage of average daily volume is between 5 and 10 % indRecord = (TradeDataTradeOpt.PctADV > 0.05 & ... TradeDataTradeOpt.PctADV <= 0.10); BasketReport.BasketCategory(i) = {'5%-10%'}; case 10 % Percentage of average daily volume is between 10 and 20 % indRecord = (TradeDataTradeOpt.PctADV > 0.10 & ... TradeDataTradeOpt.PctADV <= 0.20); BasketReport.BasketCategory(i) = {'10%-20%'}; case 11 % Percentage of average daily volume is greater than 20 % indRecord = (TradeDataTradeOpt.PctADV > 0.20); BasketReport.BasketCategory(i) = {'>20%'}; % Market cap case 12 % Large cap indRecord = (TradeDataTradeOpt.MktCap > 10000000000); BasketReport.BasketCategory(i) = {'LC'}; case 13 % Mid cap indRecord = (TradeDataTradeOpt.MktCap > 1000000000 & ... TradeDataTradeOpt.MktCap <= 10000000000); BasketReport.BasketCategory(i) = {'MC'}; case 14 % Small cap indRecord = (TradeDataTradeOpt.MktCap <= 1000000000); BasketReport.BasketCategory(i)={'SC'}; % Sectors % Description of basket category case {15, 16, 17, 18, 19, 20, 21, 22, 23, 24} j = j + 1; if j <= numSectors indRecord = strcmp(TradeDataTradeOpt.Sector,uniqueSectors(j)); BasketReport.BasketCategory(i) = uniqueSectors(j); end end % Get subset of TradeData TD = TradeDataTradeOpt(indRecord,:); if ~isempty(TD) % Covariance Matrix in $/Shares^2 CC2 = CC(indRecord,indRecord); %Trading Period Covariance Matrix in $/Shares^2 C2 = C1(indRecord,indRecord); %Annualized Covariance Matrix in $/Shares^2 RR = R(indRecord,:); %Residuals for Stocks in group % Basket Summary Calculations Weight2 = TD.Value / sum(TD.Value); % Side I_Buy = (TD.SideIndicator == 1); I_Sell = (TD.SideIndicator == -1); % Fill basket report table BasketReport.Number(i) = size(TD,1); % Number of records that match criteria BasketReport.Weight(i) = sum(TD.Value)/PortfolioValue; % Weight of assets in criteria BasketReport.MI(i) = Weight2' * TD.MI; % Market impact of assets BasketReport.TR(i) = sqrt(trace(RR'*CC2*RR)) / sum(TD.Value) * 10000; % Timing risk of assets BasketReport.POV(i) = Weight2' * TD.POV; % POV of assets BasketReport.TradeTime(i) = Weight2' * TD.TradeTime; % Tradetime of assets BasketReport.PctADV(i) = Weight2' * TD.PctADV; % Percentage of ADV BasketReport.Price(i) = Weight2' * TD.Price; % Total price of assets BasketReport.Volatility(i) = Weight2' * TD.Volatility; % Volatility BasketReport.Risk(i) = sqrt(TD.Shares' * C2 * TD.Shares) / ... sum(TD.Value); % Risk value % RC and MCR Shares2 = TradeDataTradeOpt.Shares; Shares3 = TradeDataTradeOpt.Shares; Shares2(indRecord) = 0; Shares3(indRecord) = Shares3(indRecord) * 0.90; if sum(Shares2) > 0 BasketReport.RC(i) = PortfolioRisk / sqrt(Shares2' * CD * Shares2) - 1; else BasketReport.RC(i) = 0; end BasketReport.MCR(i) = PortfolioRisk / sqrt(Shares3' * CD * Shares3) - 1; % Beta value, liquidity factor and total value BasketReport.Beta(i) = sum(Weight2 .* TD.SideIndicator .* TD.Beta); BasketReport.LF(i) = Weight2' * TD.LF; BasketReport.TotalValue(i) = sum(TD.Value); % Calculate buy share values if sum(I_Buy) > 0 BasketReport.BuyValue(i) = sum(TD.Value(I_Buy)); BasketReport.BuyShares(i) = sum(TD.Shares(I_Buy)); else BasketReport.BuyValue(i) = 0; BasketReport.BuyShares(i) = 0; end % Calculate sell share values if sum(I_Sell) > 0 BasketReport.SellValue(i) = sum(TD.Value(I_Sell)); BasketReport.SellShares(i) = sum(TD.Shares(I_Sell)); else BasketReport.SellValue(i) = 0; BasketReport.SellShares(i) = 0; end % Calculate net value of criteria and number of shares BasketReport.NetValue(i) = BasketReport.BuyValue(i) - ... BasketReport.SellValue(i); BasketReport.Shares(i) = sum(TD.Shares); end end % Remove rows with no stocks indRecord = (BasketReport.Number > 0); BasketReport = BasketReport(indRecord,:);
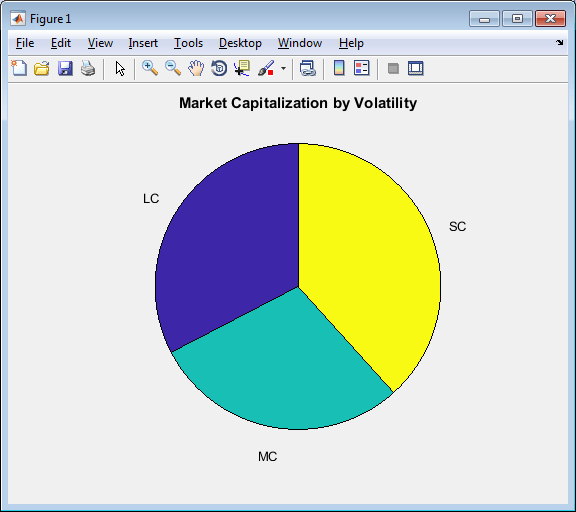
Display market capitalization by volatility as a pie chart.
pie(BasketReport.Volatility(8:10),BasketReport.BasketCategory(8:10))
title('Market Capitalization by Volatility')
Create Principal Bid Summary
Determine the efficient trading frontier by time. Use different trade time scenarios. Estimate trading costs for price appreciation, market impact, and timing risk for each scenario.
ScenarioTime = [0.10;0.25;0.50;0.75;1.0;1.50;2.0;2.5;3.0;3.5;4.0;4.5;5.0]; numScenarios = size(ScenarioTime,1); ETFCosts = zeros(numScenarios,5); TableVariableNames = TradeDataTradeOpt.Properties.VariableNames; if sum(strcmp(TableVariableNames,'DeltaP')) > 0 DeltaP = TradeDataTradeOpt.DeltaP; elseif sum(strcmp(TableVariableNames,'Alpha_bp')) > 0 DeltaP = TradeDataTradeOpt.Alpha_bp; else DeltaP = zeros(NumberStocks,1); end % Convert DeltaP from basis points per day to cents/share per period DeltaP = DeltaP / 1000 .* TradeDataTradeOpt.Price / totalNumberPeriods; for i = 1:numScenarios TradeTime = ScenarioTime(i); TradeDataTradeOpt.POV = TradeDataTradeOpt.Shares ./ ... (TradeDataTradeOpt.Shares + TradeTime .* TradeDataTradeOpt.ADV); % Price Appreciations in Dollars PA = 1/2 * TradeDataTradeOpt.Shares .* DeltaP .* TradeTime; TotPA = sum(PA) / (TradeDataTradeOpt.Shares' * ... TradeDataTradeOpt.Price) .* 10000; % bp PA = PA ./ (TradeDataTradeOpt.Shares .* ... TradeDataTradeOpt.Price) * 10000; % bp % Market Impact in Dollars MI = marketImpact(k,TradeDataTradeOpt) .* TradeDataTradeOpt.Shares .* ... TradeDataTradeOpt.Price ./ 10000; %dollars; TotMI = sum(MI) / (TradeDataTradeOpt.Shares' * ... TradeDataTradeOpt.Price) .* 10000; % bp MI = MI ./ (TradeDataTradeOpt.Shares .* ... TradeDataTradeOpt.Price) * 10000; % bp % Timing Risk in Dollars TotTR = sqrt(1/3 * TradeDataTradeOpt.Shares' * ... (CD * TradeTime) * TradeDataTradeOpt.Shares) / ... (TradeDataTradeOpt.Shares' * TradeDataTradeOpt.Price) * 10000; % Total Cost Dollars TotTC = (TotMI + TotPA); % ETF Cost Table ETFCosts(i,1) = TradeTime; ETFCosts(i,2) = TotMI; ETFCosts(i,3) = TotPA; ETFCosts(i,4) = TotTC; ETFCosts(i,5) = TotTR; end % Save as Table ETFCosts = table(ETFCosts(:,1),ETFCosts(:,2),ETFCosts(:,3),ETFCosts(:,4), ... ETFCosts(:,5),'VariableNames',{'Days','MI_bp','PA_bp','TotalCost_bp', ... 'TR_bp'});
Determine the trade time with the lowest total cost.
mintotcost = min(ETFCosts.TotalCost_bp); for i = 1:numScenarios if(ETFCosts.TotalCost_bp(i) == mintotcost) scenario = ETFCosts.Days(i); end end scenario
scenario =
5For details about the preceding calculations, contact the Kissell Research Group.
References
[1] Kissell, Robert. The Science of Algorithmic Trading and Portfolio Management. Cambridge, MA: Elsevier/Academic Press, 2013.
[2] Malamut, Roberto. “Multi-Period Optimization Techniques for Trade Scheduling.” Presentation at the QWAFAFEW New York Conference, April 2002.
[3] Kissell, Robert, and Morton Glantz. Optimal Trading Strategies. New York, NY: AMACOM, Inc., 2003.
See Also
krg | liquidityFactor | marketImpact