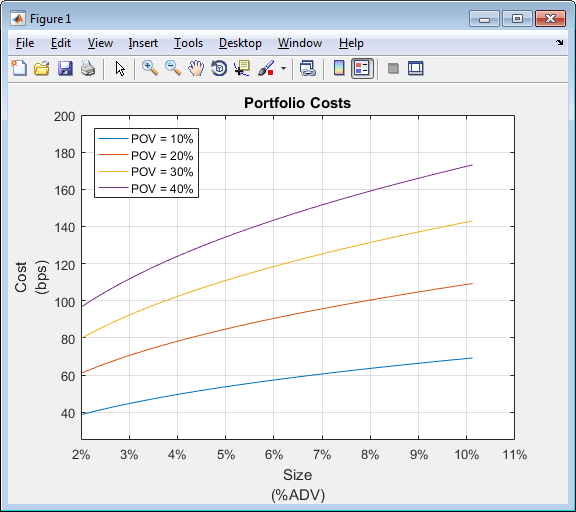
portfolioCostCurves
Estimate market-impact cost of order execution for portfolio
Description
pcc = portfolioCostCurves(k,portfolio,tradeQuantity,tqRange,tradeStrategy,tsRange)
Kissell Research Group (KRG) transaction cost analysis object
kPortfolio data
portfolioTrade quantity
tradeQuantitywith a range of valuestqRangeTrade strategy
tradeStrategywith a range of valuestsRange
Examples
Input Arguments
Output Arguments
Tips
To test multiple portfolio transactions, you can use different ranges. You can change the percentage of shares in the transaction or use a different trade strategy. For details, see Input Arguments.
For details about the calculations, contact Kissell Research Group.
References
[1] Kissell, Robert. “A Practical Framework for Transaction Cost Analysis.” Journal of Trading. Vol. 3, Number 2, Summer 2008, pp. 29–37.
[2] Kissell, Robert. “Algorithmic Trading Strategies.” Ph.D. Thesis. Fordham University, May 2006.
[3] Kissell, Robert. “TCA in the Investment Process: An Overview.” Journal of Index Investing. Vol. 2, Number 1, Summer 2011, pp. 60–64.
[4] Kissell, Robert. The Science of Algorithmic Trading and Portfolio Management. Cambridge, MA: Elsevier/Academic Press, 2013.
[5] Kissell, Robert, and Morton Glantz. Optimal Trading Strategies. New York, NY: AMACOM, Inc., 2003.
Version History
Introduced in R2016a
See Also
krg | costCurves | iStar | marketImpact | timingRisk