Detect Anomalies in Signals Using deepSignalAnomalyDetector

Case 1: Detect Abnormal Heartbeat Sequences

This section uses the deepSignalAnomalyDetector object to detect abnormal heartbeat sequences in data from the BIDMC Congestive Heart Failure Database [1]. The heartbeat collection has 5405 electrocardiogram (ECG) sequences of varying length, each sampled at 250 Hz and containing three categories of heartbeat:

The data is labeled, but in this example you use the labels only for testing and performance evaluation. The autoencoder training process is fully unsupervised.

Load Data

Download the heartbeat data from https://ssd.mathworks.com/supportfiles/SPT/data/PhysionetBIDMC.zip using the downloadSupportFile function. The whole data set is approximately 2 MB in size. The ecgSignals contains signals and ecgLabels contains labels.

datasetZipFile = matlab.internal.examples.downloadSupportFile('SPT','data/PhysionetBIDMC.zip');
datasetFolder = fullfile(fileparts(datasetZipFile),'PhysionetBDMC');
if ~exist(datasetFolder,'dir')     
    unzip(datasetZipFile,datasetFolder);
end
ds1 = load(fullfile(datasetFolder,"chf07.mat"));
ecgSignals1 = ds1.ecgSignals

ecgSignals1=5405×1 cell array
    {146×1 double}
    {140×1 double}
    {139×1 double}
    {143×1 double}
    {143×1 double}
    {145×1 double}
    {147×1 double}
    {139×1 double}
    {143×1 double}
    {139×1 double}
    {146×1 double}
    {143×1 double}
    {144×1 double}
    {142×1 double}
    {142×1 double}
    {140×1 double}
      ⋮

ecgLabels1 = ds1.ecgLabels;
cnts = countlabels(ecgLabels1)

cnts=3×3 table
    Label    Count    Percent
    _____    _____    _______

      N      5288      97.835
      V         6     0.11101
      r       111      2.0537

Visualize typical waveforms corresponding to each of the three heartbeat categories.

helperPlotECG(ecgSignals1,ecgLabels1)

Get the indices corresponding to each category and split the data set into training and testing sets. In the training set, include 60% of samples to maintain the natural anomaly distribution. Exclude class V samples from the training set but include them in the test set. Including these samples in the test set determines whether the autoencoder can detect previously unobserved anomaly types.

idxN = find(strcmp(ecgLabels1,"N"));
idxR = find(strcmp(ecgLabels1,"r"));
idxV = find(strcmp(ecgLabels1,"V"));
idxs = splitlabels(ecgLabels1,0.6,Exclude="V");
idxTrain = [idxs{1}];
idxTest = [idxs{2};idxV];

countlabels(ecgLabels1(idxTrain))

ans=2×3 table
    Label    Count    Percent
    _____    _____    _______

      N      3173     97.932 
      r        67     2.0679 

countlabels(ecgLabels1(idxTest))

ans=3×3 table
    Label    Count    Percent
    _____    _____    _______

      N      2115      97.691
      V         6     0.27714
      r        44      2.0323

Create and Train Detector

Create a deepSignalAnomalyDetector object with a long short-term memory (LSTM) model. Set WindowLength to "fullSignal" to determine whether each complete signal segment is normal or abnormal.

DLSTM1 = deepSignalAnomalyDetector(1,"lstm",WindowLength="fullSignal")

DLSTM1 = 
  deepSignalAnomalyDetectorLSTM with properties:

                IsTrained: 0
              NumChannels: 1

   Model Information
                ModelType: 'lstmautoencoder'
       EncoderHiddenUnits: [32 16]
       DecoderHiddenUnits: [16 32]

   Threshold Information
                Threshold: []
          ThresholdMethod: 'contaminationFraction'
       ThresholdParameter: 0.0100

   Window Information
             WindowLength: 'fullSignal'
    WindowLossAggregation: 'mean'

Train the detector using the adaptive moment estimation (Adam) optimizer, which is one of the most popular solvers for deep learning training. The maximum number of epochs often needs to be adjusted according to the data set size and training process. Because the number of samples is large, set MaxEpochs to 200.

opts = trainingOptions("adam", ...
    MaxEpochs=200, ...
    MiniBatchSize=500);
trainDetector(DLSTM1,ecgSignals1(idxTrain),opts);

    Iteration    Epoch    TimeElapsed    LearnRate    TrainingLoss
    _________    _____    ___________    _________    ____________
            1        1       00:00:00        0.001         0.21702
           50        9       00:00:23        0.001        0.045203
          100       17       00:00:46        0.001        0.038362
          150       25       00:01:09        0.001        0.029108
          200       34       00:01:32        0.001         0.02876
          250       42       00:01:58        0.001        0.027447
          300       50       00:02:21        0.001        0.026755
          350       59       00:02:45        0.001        0.028011
          400       67       00:03:08        0.001        0.026707
          450       75       00:03:32        0.001        0.025835
          500       84       00:03:56        0.001        0.027199
          550       92       00:04:20        0.001        0.026517
          600      100       00:04:43        0.001        0.026001
          650      109       00:05:07        0.001        0.026268
          700      117       00:05:30        0.001        0.027192
          750      125       00:05:53        0.001        0.025325
          800      134       00:06:16        0.001        0.026108
          850      142       00:06:40        0.001        0.025687
          900      150       00:07:04        0.001         0.02498
          950      159       00:07:27        0.001        0.030483
         1000      167       00:07:51        0.001        0.026577
         1050      175       00:08:25        0.001        0.025216
         1100      184       00:08:49        0.001        0.025874
         1150      192       00:09:13        0.001        0.025275
         1200      200       00:09:37        0.001        0.019067
Training stopped: Max epochs completed
Computing threshold...
Threshold computation completed.

Adjust Threshold

By default, the deepSignalAnomalyDetector object computes the threshold assuming that 1% of the data in the training set are abnormal. This assumption is not always true, so you often need to adjust the threshold by changing the automatic threshold method or by setting the threshold value manually.

Use the plotLoss (Signal Processing Toolbox) function to visualize the losses of the training set and the current threshold value. Each stem corresponds to the reconstruction error for one of the signals in the training data set.

figure
plotLoss(DLSTM1,ecgSignals1(idxTrain))
ylim([0,0.1])

Based on the plotLoss output, set threshold value manually such that the few sporadic losses that exceed the threshold are most likely anomalies.

updateDetector(DLSTM1, ...
    ThresholdMethod="Manual", ...
    Threshold=0.03)

To validate the choice of threshold, plot the distribution of the reconstruction errors for the normal and the abnormal data using plotLossDistribution (Signal Processing Toolbox). The histogram to the left of the threshold corresponds to the distribution of normal data. The histogram to the right of the threshold corresponds to the distribution of abnormal data. The chosen threshold value successfully separates the normal and abnormal groups.

% ecgSignals1(idxN) contains normal signals only
% ecgSignals1([idxR;idxV]) contains abnormal signals
plotLossDistribution(DLSTM1,ecgSignals1(idxN),ecgSignals1([idxR; idxV]))

Detect Anomalies and Evaluate Performance

Pick one sample from each category in the testing set and plot the reconstructed signal using plotAnomalies (Signal Processing Toolbox). The red lines represent signals the detector classifies as abnormal. A good sign that the detector is successfully trained is that it can adequately reconstruct normal signals and cannot adequately reconstruct abnormal signals.

figure(Position=[0 0 500 300])
idxNTest = union(idxN,idxTest); % Class N
plotAnomalies(DLSTM1,ecgSignals1(idxNTest(1)),PlotReconstruction=true)

figure(Position=[0 0 500 300])
idxVTest = union(idxV,idxTest); % Class V
plotAnomalies(DLSTM1,ecgSignals1(idxVTest(1)),PlotReconstruction=true)

figure(Position=[0 0 500 300])
idxRTest = union(idxR,idxTest); % Class r
plotAnomalies(DLSTM1,ecgSignals1(idxRTest(1)),PlotReconstruction=true)

Use the detect (Signal Processing Toolbox) object function of the detector with both training and testing sets to detect anomalies and compute reconstruction losses.

[labelsTrainPred1,lossTrainPred1] = detect(DLSTM1,ecgSignals1(idxTrain));
[labelsTestPred1,lossTestPred1] = detect(DLSTM1,ecgSignals1(idxTest));

There are two different anomaly detection tasks.

Analyze the performance of the trained autoencoder in the two tasks.

You can use a receiver operating characteristic (ROC) curve to evaluate the accuracy of a detector over a range of decision thresholds. The area under the ROC curve (AUC) measures the overall performance. The closer the AUC is to 1, the stronger the detection ability of the detector. Compute the AUC using the rocmetrics function. The AUC is close to one for the outlier detection, and slightly smaller but still very good for the novelty detection.

figure("Position",[0 0 600 300])
tiledlayout(1,2,TileSpacing="compact")
nexttile
rocc = rocmetrics(ecgLabels1(idxTrain)~="N",cell2mat(lossTrainPred1),true);
plot(rocc,ShowModelOperatingPoint=false)
title(["Training Set ROC Curve","(Outlier Detection)"])
nexttile
rocc = rocmetrics(ecgLabels1(idxTest)~="N",cell2mat(lossTestPred1),true);
plot(rocc,ShowModelOperatingPoint=false)
title(["Testing Set ROC Curve","(Novelty Detection)"])

Compute the detection accuracy with the previously specified threshold.

figure("Position",[0 0 1000 300])
tiledlayout(1,2,TileSpacing="compact")
nexttile
cm = confusionchart(ecgLabels1(idxTrain)~="N",cell2mat(labelsTrainPred1));
cm.RowSummary = "row-normalized";
title("Training Set Accuracy (Outlier Detection)")
nexttile
cm = confusionchart(ecgLabels1(idxTest)~="N",cell2mat(labelsTestPred1));
cm.RowSummary = "row-normalized";
title("Test Set Accuracy (Novelty Detection)")

Case 2: Detect Anomalous Points in Continuous Long Time Series

The previous section showed how to detect anomalies in data sets containing multiple signal segments and determine whether each segment was abnormal or not. In this section the data set is a single signal. The goal is to detect anomalies in the signal and the times at which they occur.

Use a deepSignalAnomalyDetector on a long ECG recording to detect anomalies caused by ventricular tachycardia. The data is from the Sudden Cardiac Death Holter Database [2]. The ECG signal has a sampling rate of 250 Hz.

Download and Prepare Data

Download the data from https://ssd.mathworks.com/supportfiles/SPT/data/PhysionetSDDB.zip using the downloadSupportFile function. The data set contains two timetables. The timetable X contains the ECG signal. Timetable Y contains labels that indicate whether each sample of the ECG signal is normal. As in the previous section, you use the labels only to verify the accuracy of the detector.

datasetZipFile = matlab.internal.examples.downloadSupportFile('SPT','data/PhysionetSDDB.zip');
datasetFolder = fullfile(fileparts(datasetZipFile),'PhysionetSDDB');
if ~exist(datasetFolder,'dir')     
    unzip(datasetZipFile,datasetFolder);
end
ds2 = load(fullfile(datasetFolder,"sddb49.mat"));
ecgSignals2 = ds2.X;
ecgLabels2 = ds2.y;

Normalize the full signal and visualize it. Overlay the located anomalies. The anomaly detection in this case is challenging because, as often happens in ECG recordings, the signal baseline drifts. These changes in baseline level can easily be misclassified as anomalies.

A common approach to choose training data is to use a segment of the signal where it is evident that there are no anomalies. In many situations, the beginning of a recording is usually normal, such as in this ECG signal. Choose the first 200 seconds of the recording to train the model with purely normal data. Use the rest of the recording to test the performance of the anomaly detector. The training data contain segments with baseline drift, ideally, the detector learns and adapts to this pattern and considers it normal.

dataProcessed = normalize(ecgSignals2);
figure
plot(dataProcessed.Time,dataProcessed.Variables)
hold on
plot(dataProcessed(ecgLabels2.anomaly,:).Time,dataProcessed(ecgLabels2.anomaly,:).Variables,".")
hold off
xlabel("Time (s)")
ylabel("Normalized ECG Amplitude")
title("sddb49 ECG Signal")
legend(["Signal" "Anomaly"])

Split the data set into training and testing sets.

fs = 250;
idxTrain2 = 1:200*fs;
idxTest2 =idxTrain2(end)+1:height(dataProcessed);
dataProcessedTrain = dataProcessed(idxTrain2,:);
labelsTrainTrue = ecgLabels2(idxTrain2,:);
dataProcessedTest = dataProcessed(idxTest2,:);
labelsTestTrue = ecgLabels2(idxTest2,:);

Create and Train Detector

Create a deepSignalAnomalyDetector with a convolutional autoencoder model.

The training set contains only normal data. So, it is reasonable to use the maximum reconstruction error as a threshold when declaring a signal segment to be an anomaly. Set the ThresholdMethod property to "max". To incorporate the complexity of the signal due to baseline drift, use a larger network than the default. To detect anomalies over each sample of the signal, keep the window length to its default value of one sample.

DCONV2 = deepSignalAnomalyDetector(1,"conv", ...
    FilterSize=32, ...
    NumFilters=16, ...
    NumDownsampleLayers=4, ...
    ThresholdMethod="max")

DCONV2 = 
  deepSignalAnomalyDetectorCNN with properties:

                IsTrained: 0
              NumChannels: 1

   Model Information
                ModelType: 'convautoencoder'
               FilterSize: 32
               NumFilters: 16
      NumDownsampleLayers: 4
         DownsampleFactor: 2
       DropoutProbability: 0.2000

   Threshold Information
                Threshold: []
          ThresholdMethod: 'max'
       ThresholdParameter: 1

   Window Information
             WindowLength: 1
            OverlapLength: 'auto'
    WindowLossAggregation: 'mean'

To ensure full training of the large network, set the maximum number of epochs to 500. To plot training progress during training instead of presenting it in a table, set the Plots training option to "training-progress" and Verbose to false.

opts = trainingOptions("adam",MaxEpochs=500,Plots="training-progress",Verbose=false);
trainDetector(DCONV2,dataProcessedTrain,opts)

Detect Anomalies and Evaluate Performance

Plot the reconstruction error distribution of the test signal and compare it to ground truth labels. There is an obvious high loss peak corresponds to the location of an anomaly. The distribution also contains multiple smaller fluctuations.

figure
tiledlayout(2,1)
nexttile
plotLoss(DCONV2,dataProcessed(idxTest2,:));
nexttile
stem(ecgLabels2{idxTest2,:},".")
grid on
yticks([0 1])
yticklabels({"Normal","Abnormal"})
title("Ground Truth Labels")
xlabel("Window Index")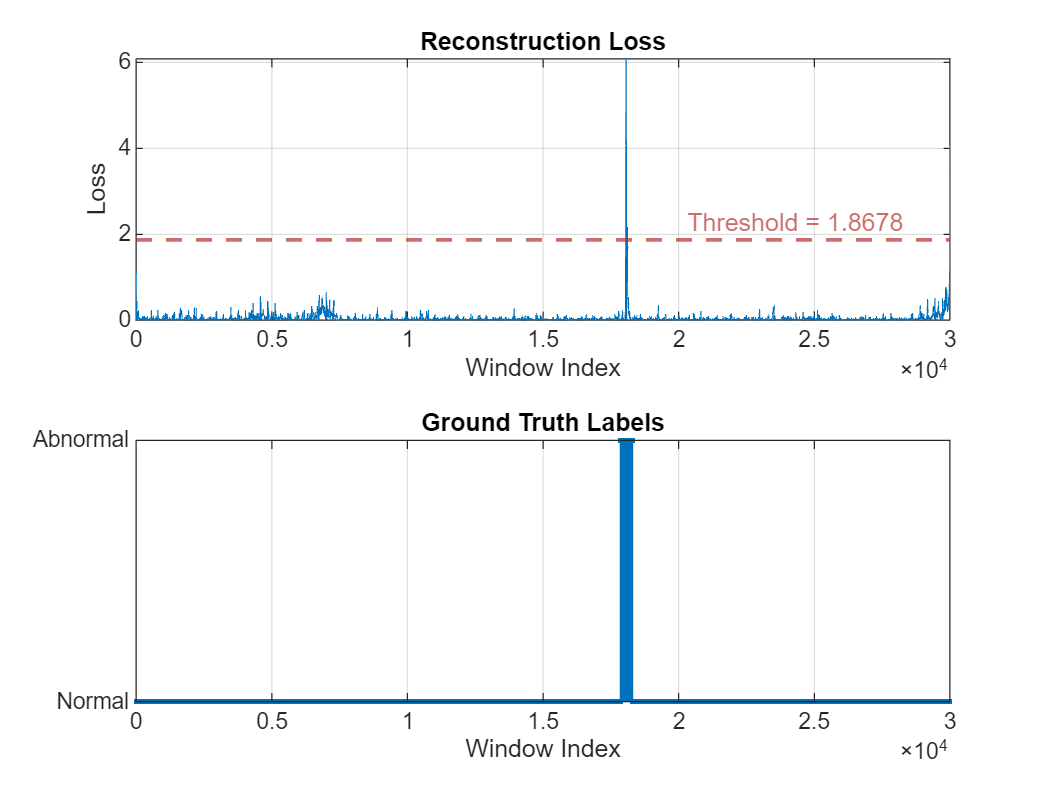

View the signal reconstruction in a region of the test set with abnormal heartbeats and in a region of the test set with baseline drift. The reconstructed signal follows the baseline very well and deviates from the original signal only at anomaly points.

plotAnomalies(DCONV2,dataProcessed(250*fs:300*fs,:),PlotReconstruction=true)
title("Test Region with Abnormal Heartbeats")
grid on

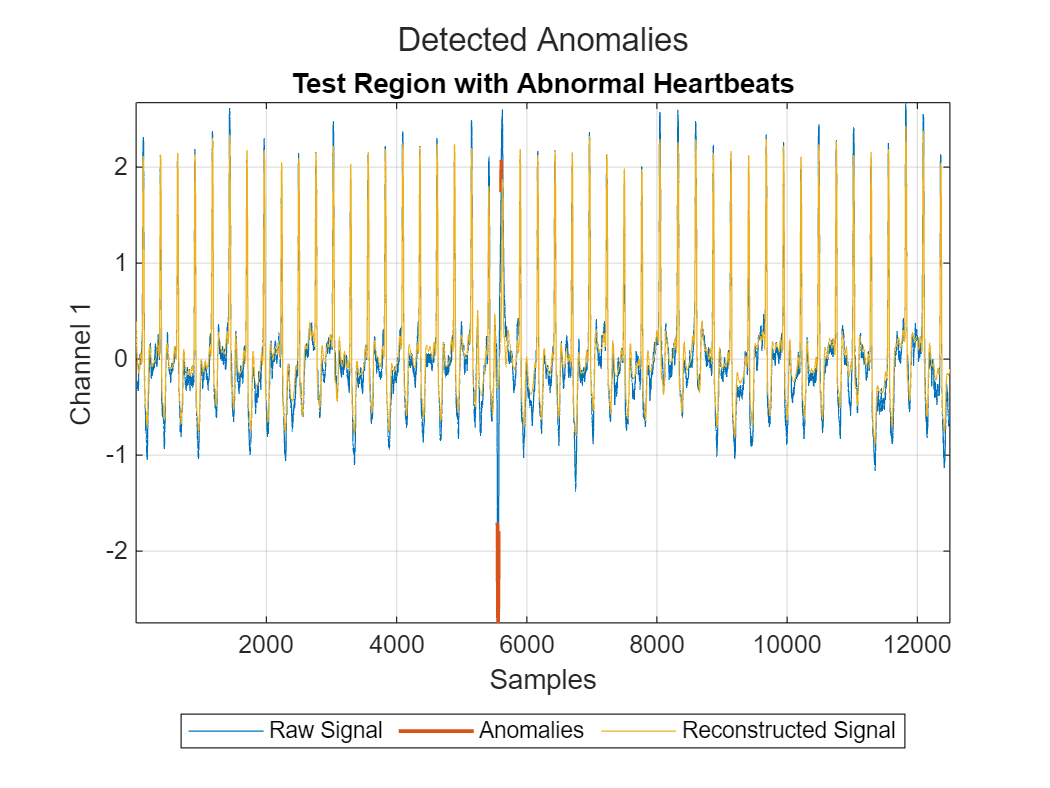
plotAnomalies(DCONV2,dataProcessed(210*fs:250*fs,:),PlotReconstruction=true)
title("Test Region with Baseline Drift")

Case 3: Detect Anomalous Regions in Multichannel Signals

There are scenarios where the data contains multiple signals coming from different measurements. These signals can include acceleration, temperature, and the rotational speed of a motor. You can train the deepSignalAnomalyDetector object with multivariate signals and detect anomalies in these multi-measurement observations.

Load and Prepare Data

Load the waveform data set WaveformData. The observations are arrays of size numChannels-by-numTimeSteps, where numChannels is the number of channels and numTimeSteps is the number of time steps in the sequence. Transpose the arrays so that the columns correspond to the time steps. Display the first few cells of the data.

load WaveformData
head(data)

    {103×3 double}
    {136×3 double}
    {140×3 double}
    {124×3 double}
    {127×3 double}
    {200×3 double}
    {141×3 double}
    {151×3 double}

Visualize the first few sequences in a plot.

numChannels = size(data{1},2);
tiledlayout(2,2)
for ii = 1:4
    nexttile
    stackedplot(data{ii},DisplayLabels="Channel " + (1:numChannels));
    title("Observation " + ii)
    xlabel("Time Step")
end

Partition the data into training and test partitions. Use 90% of the data for training and 10% for testing.

numObservations = numel(data);
rng default
[idxTrain3,~,idxTest3] = dividerand(numObservations,0.9,0,0.1);
signalTrain3 = data(idxTrain3);
signalTest3 = data(idxTest3);

Create and Train Detector

Create a default anomaly detector and specify the number of channels as 3.

DCONV3 = deepSignalAnomalyDetector(3,'lstmf',WindowLen = 5);
trainDetector(DCONV3,signalTrain3)

    Iteration    Epoch    TimeElapsed    LearnRate    TrainingLoss
    _________    _____    ___________    _________    ____________
            1        1       00:00:00        0.001          1.3197
           50        8       00:00:05        0.001         0.74277
          100       15       00:00:11        0.001         0.50886
          150       22       00:00:16        0.001         0.44456
          200       29       00:00:21        0.001          0.4038
          210       30       00:00:22        0.001         0.41962
Training stopped: Max epochs completed
Computing threshold...
Threshold computation completed.

Detect Anomalies and Evaluate Performance

To test the detector, select 50 data sequences at random and add artificial anomalies to them. Randomly select 50 of the sequences to modify.

signalTest3New = signalTest3;
numAnomalousSequences = 50;
rng default
idx = randperm(numel(signalTest3),numAnomalousSequences);

Select a 20-sample region in a random channel of each chosen sequence and replace it with five times the absolute value of its amplitude.

for ii = 1:numAnomalousSequences
    X = signalTest3New{idx(ii)};
    idxPatch = 40:60;
    nch = randi(3);
    OldRegion = X(idxPatch,nch);
    newRegion = 5*abs(OldRegion);
    X(idxPatch,nch) = newRegion;
    signalTest3New{idx(ii)} = X;
end

Use the anomaly detector to find the anomalous regions. Visualize the results for two of the signals. The detector determines that an anomaly exists in a signal when any of its channels shows abnormal behavior.

figure
plotAnomalies(DCONV3,signalTest3New{idx(2)})

figure
plotAnomalies(DCONV3,signalTest3New{idx(20)})

Conclusion

This example shows how to use a deepSignalAnomalyDetector object trained without labels to detect point, region, or observation anomalies in signal segments, long signals, and multivariate signals.

References

[1] Donald S. Baim, Wilson S. Colucci, E. Scott Monrad, Harton S. Smith, Richard F. Wright, Alyce Lanoue, Diane F. Gauthier, Bernard J. Ransil, William Grossman W, and Eugene Braunwald. “Survival of Patients with Severe Congestive Heart Failure Treated with Oral Milrinone.” Journal of the American College of Cardiology, vol. 7, no. 3, (March 1986): 661–70. https://doi.org/10.1016/S0735-1097(86)80478-8.

[2] Greenwald, Scott David. "Development and analysis of a ventricular fibrillation detector." (M.S. thesis, MIT Dept. of Electrical Engineering and Computer Science, 1986).

[3] Goldberger, Ary L., Luis A. N. Amaral, Leon Glass, Jeffrey M. Hausdorff, Plamen Ch. Ivanov, Roger G. Mark, Joseph E. Mietus, George B. Moody, Chung-Kang Peng, and H. Eugene Stanley. “PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals.” Circulation 101, no. 23 (June 13, 2000): https://doi.org/10.1161/01.CIR.101.23.e215

Supporting Function

function helperPlotECG(ecgData,ecgLabels)
    figure(Position=[0 0 900 250])
    tiledlayout(1,3,TileSpacing="compact");
    classes = {"N","r","V"};
    for i=1:length(classes)
        x = ecgData(ecgLabels==classes{i});
        nexttile
        plot(x{4})
        xticks([0 70 length(x{4})])
        axis tight
        title("Signal with class "+classes{i})
    end
end